3.Квадратурные формулы.

Постановка задачи численного интегрирования.

Пусть требуется вычислить

Если - первообразная для , то . Часто получить выражение для первообразной не удается. Подынтегральная функция может быть задана в табличном виде. В этих случаях подынтегральную функцию заменяют на некоторую аппроксимирующую функцию, интеграл от которой легко вычисляется в элементарных функциях. Во многих случаях формулы для приближенного вычисления интегралов можно записать в виде

Формулы такого вида называются квадратурными.

- узлы квадратурной формулы.

- коэффициенты.

- погрешность (остаточный член ) квадратурной формулы.

Формула прямоугольников.

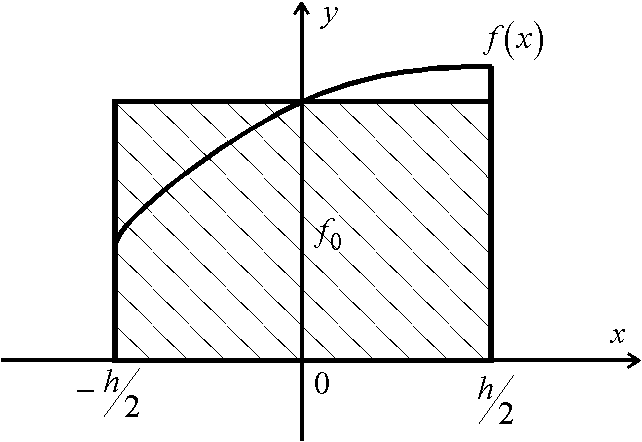
Допустим, что . Положим приближенно

(3)

где , т.е. площадь криволинейной трапеции, ограниченной сверху графиком функции , аппроксимируется площадью прямоугольника, высота которого равна значению в средней точке основания трапеции .

Погрешность формулы (3) для этого случая,

Формула трапеций.

Пусть Полагаем

(4)

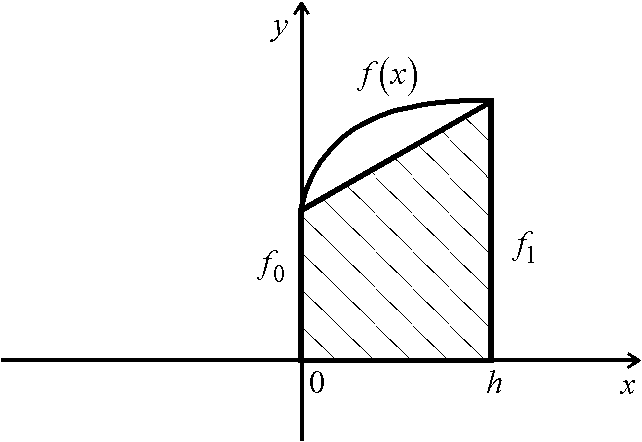г де т.е. интеграл приближенно заменяется площадью заштрихованной трапеции, показанной на рисунке.

Погрешность формулы (3) для этого случая,

Формула Симпсона .

Предположим, что Интеграл приближенного заменяем площадью заштрихованной криволинейной трапеции, ограниченной сверху параболой, проходящей через точки де

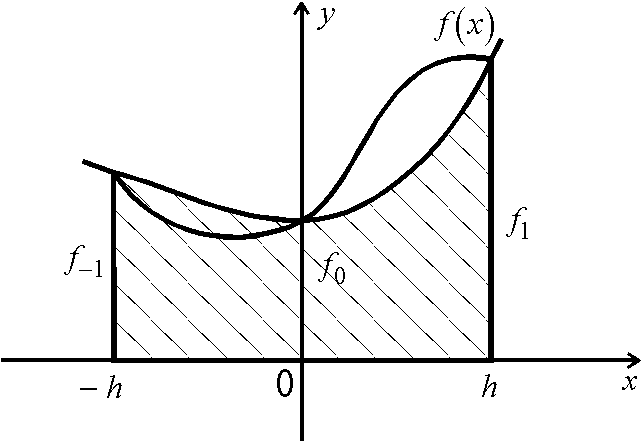
Указанная парабола задается уравнением

в чем нетрудно убедиться, положив поочередно . Отсюда находим

Таким образом , формула Симпсона , называемая также формулой парабол , имеет вид

Погрешность формулы для этого случая,

4. Имеется большое число частных случаев дифференциальных уравнений, которые можно проинтегрировать в конечном виде; однако большинство задач с дифференциальными уравнениями может быть решено только численно. Простейшим методом решения является метод Эйлера, легко реализуемый графически.

Метод Эйлера.

Пусть задано

Схему вычислений зададим следующим образом:

...................

и т.д..

Ошибка обрыва для этого метода h²

Методы типа Рунге-Кутта

Если в формуле ломаной Эйлера заменить на более общее выражение , то возникает общая формула одношагового метода.

Здесь строится как весовое среднее значений функции в определенным образом выбираемых точках так, что порядок ошибки обрыва имеет порядок выше h².

Так, в простейшем методе Рунге-Кутта 3-его порядка

.

В этом случае порядок ошибки обрыва  h³.

Метод Рунге-Кутта IV порядка.

В методе Рунге-Кутта IV порядка

, где , , .

В этом случае порядок ошибки обрыва  h⁴.

Если кривые решения являются достаточно гладкими и известны некоторые начальные значения, то точность аппроксимации может быть увеличена благодаря использованию многошаговых методов.

Решение систем дифференциальных уравнений.

Задача Коши заключается в решении системы обыкновенных дифференциальных уравнений первого порядка, представляемых в виде:

где j = 1N - номер каждой зависимой переменной , x – независимая переменная. Решение ищется при заданных начальных условиях – x = x₀:

Дифференциальное уравнения высшего порядка:

с заданными начальными условиями

где (n) – порядок уравнения может быть сведено к системе дифференциальных уравнений 1-го порядка с помощью преобразований:

следовательно, решение уравнения высшего порядка также сводится к решению системы дифференциальных уравнений первого порядка.

Для численного интегрирования вышеприведенной системы может быть использован простейший метод – метод Эйлера, который реализуется формулой:

,

Этот метод обладает большой погрешностью и имеет систематическое накопление ошибок. Погрешность обрыва для метода h².

Для получения лучшего приближения может быть использован один из методов Рунге-Кутта, который применяется к каждому из уравнений системы.