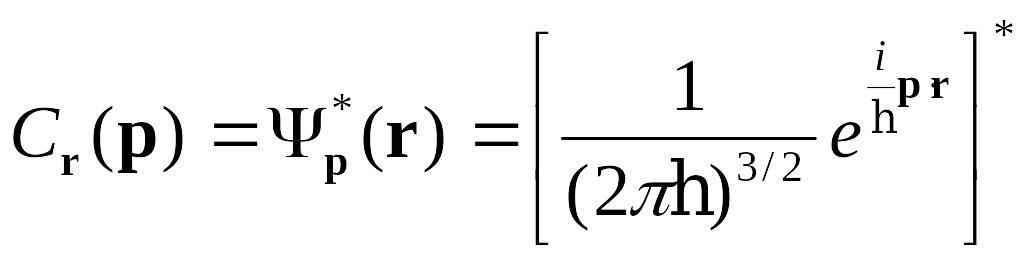- •Глава 1. Введение.
- •§ 1.1 Вариация и ее свойства.
- •§ 1.2 Уравнение Эйлера.
- •§ 1.3 Функционалы вида
- •§ 1.4 Функционалы, зависящие от производных более высокого порядка
- •§ 1.5 Задача о брахистохроне.
- •§ 1.6 Задача Дидоны.
- •Глава 2.
- •§2.1 Тензор напряжения и деформации.
- •§2.2 Тензор дисторсии. Тензор деформаций.
- •§2.3 Тензор напряжений.
- •§2.4 Закон Гука.
- •§2.5 Тензор модулей упругости изотропной среды.
- •Глава 3. §3.1 Интегральные операторы в квантовой механике.
- •§3.2 Интегральный оператор канонического преобразования.
- •§3.3 Каноническое преобразование оператора.
- •§3.4 Унитарные инварианты в квантовой механике.
- •§3.5 Матричная форма задачи о линейном гармоническом осцилляторе (лго). Матричные элементы операторов в методе Шредингера и Гайзенберга (энергетическое представление).
- •§3.6 Уравнение Паули Мы писали волновое уравнение в виде
- •§3.7 Обменное взаимодействие
- •§3.8 Основное состояние атома гелия.
- •Факультатив
- •§1 Упругие волны в изотропной среде.
- •§2 Тензорная функция Грина волнового уравнения.
- •§3 Уравнение состояния квантового идеального газа. Обменные эффекты.
- •§4 Расчет параметров вырожденного электронного газа.
- •§5 Вырожденный Бозе-газ – квазиклассическое приближение.
- •§6 Плотность вероятности для энергии системы, описываемой каноническим распределением Гиббса.
- •§7 Аппроксимация Гауссовым законом распределения вероятностей для экстенсивного термодинамического параметра.
- •§8 Статистическое описание флуктуаций интенсивного термодинамического параметра.
- •§9 Случай нескольких термодинамических параметров.
- •§10 Многомерное Гауссово распределение.
- •§11 Расчёт флуктуаций термодинамических величин.
- •§12 Расчет термодинамических величин вырожденного Бозе-газа.
- •§13 Расчёт основных термодинамических величин фотонного газа.
- •§14 Метод (представление) Шредингера. Оператор эволюции и его свойства.
- •§15 Метод (представление) Гайзенберга. Уравнение движения для оператора.
- •§17 Уравнение Шредингера в матричной форме.
- •§18 Энергетическое представление в случае дискретного спектра: волновая функция, оператор и их свойства.
- •§19 Энергетическое представление в случае дискретного спектра: методы Шредингера и Гайзенберга.
- •§20 Операторы рождения и уничтожения в задаче о лго (линейном гармоническом осцилляторе).
- •§21 Свойства оператора рождения и уничтожения.
- •§22 Волновая функция в - представлении.
- •§23 Оператор f в - представлении.
- •§24 Операторы рождения и уничтожения частиц.
- •§25 Схема Юнга квантовой механики.
Глава 3. §3.1 Интегральные операторы в квантовой механике.
Оператор
в
![]() -
представлении
-
представлении
![]() .
.
![]()
В общем случае
![]()
Здесь
![]() - ядро интегрального оператора в
координатном представлении.
- ядро интегрального оператора в
координатном представлении.
Задача на собственные функции и собственные значения
![]()
Здесь
![]() и
изменяются непрерывно.
и
изменяются непрерывно.
![]()
Разложение
функции
![]() по базису
по базису
![]() :
:
![]() ,
,
где
![]()
Тогда
![]()
и аналогично
![]()
Для того чтобы найти ядро интегрального оператора, разложим - функцию по базису собственных функций из задачи на собственные функции и собственные значения.
![]() ={т.
к. оператор от q ,
а интеграл по f, то
ставим оператор
под знак интеграла}
={т.
к. оператор от q ,
а интеграл по f, то
ставим оператор
под знак интеграла}![]() {из
задачи на собственные функции и
собственные значения }=
{из
задачи на собственные функции и
собственные значения }=![]() .
.
Поменяем порядок интегрирования
![]()
Ядро интегрального оператора
![]()
Оператору
поставили в соответствие ядро
![]() .
Тогда можно записать действие оператора
на любую функцию, решив задачу на
собственные функции и собственные
значения.
.
Тогда можно записать действие оператора
на любую функцию, решив задачу на
собственные функции и собственные
значения.
Пусть есть эрмитов оператор
![]() .
.
Тогда
![]()
А в силу равенства имеем
![]()
Найдем ядро
оператора
![]() в координатном представлении. Действие
в этом представлении сводится к умножению
на
.
в координатном представлении. Действие
в этом представлении сводится к умножению
на
.
![]()
Мы знаем, что
по определению
![]() -функции:
-функции:
![]()
Тогда
![]()
Ядро оператора координат в координатном представлении
![]()
Ядро оператора
![]() в
-представлении,
тогда имеет вид
в
-представлении,
тогда имеет вид
![]()
§3.2 Интегральный оператор канонического преобразования.
Можно решать задачу в разных представлениях. Преобразование, осуществляющее замену переменных, в которых рассматривается задача, называется каноническим преобразованием.
Запишем:
![]() (*)
(*)
![]() (**)
(**)
Сравним эти равенства с:
Тогда
![]() можно рассматривать как ядро некоторого
интегрального преобразования, переводящего
- представление в
-представление.
можно рассматривать как ядро некоторого
интегрального преобразования, переводящего
- представление в
-представление.
Обозначим
![]() ,
,
где
![]()
Собственная
функция оператора
в
-представлении
играет роль ядра интегрального оператора
![]() ,
осуществляющего преобразование от
,
осуществляющего преобразование от
![]() к
.
к
.
Аналогично
![]()
![]()
Из соотношения (*) следует, что для того чтобы говорить о функции надо знать коэффициенты разложения . Т. е. зная можем записать :
![]()
Чтобы знать коэффициенты надо знать - это следует из (**)
![]()
Тогда задать
состояние мы можем либо функцией
![]() ,
либо функцией
,
либо функцией
![]() .
Эту информацию мы задаем в разложении
переменных.
.
Эту информацию мы задаем в разложении
переменных.
Оператор осуществляет переход от переменных к переменным:
![]() .
.
Это есть каноническое преобразование переменных.
Установим связь
между
![]() и
:
и
:
![]() ,
,
![]() ,
,
подставим одно в другое
![]() ,
,
тогда
![]() (***)
(***)
Д.З. записать это равенство на языке ядер.
Распишем:
![]()
также
![]()
Этому соответствует соотношение операторов
![]()
Из (***) следует
![]() ,
тогда
,
тогда
![]() ,
,
отсюда
![]()
получили, что оператор унитарный.
Рассмотрим норму функции и обнаружим унитарность:
![]() {используем
равенство Парсеваля}
{используем
равенство Парсеваля}![]() ,
,
тогда
![]() ,
,
![]() .
.
Равенство Парсеваля:
![]() .
.
Мы знаем, что ядро оператора
![]() ,
,
есть собственная функция оператора в - представлении.
Тогда ядро оператора :
![]() ,
,
есть собственная функция оператора в -представлении.
Но
![]() .
.
Задачи на собственные функции и собственные значения имеют вид:
![]() ,
,
![]() .
.
![]() -собственная функция оператора
в
-представлении
есть комплексно сопряженная собственная
функция оператора
в
-
представлении.
-собственная функция оператора
в
-представлении
есть комплексно сопряженная собственная
функция оператора
в
-
представлении.
Отсюда запишем: