§2.4 Закон Гука.

Тензоры напряжения и деформаций могут быть определены через термодинамические характеристики – свободную энергию и термодинамический потенциал Гиббса единицы объема среды:

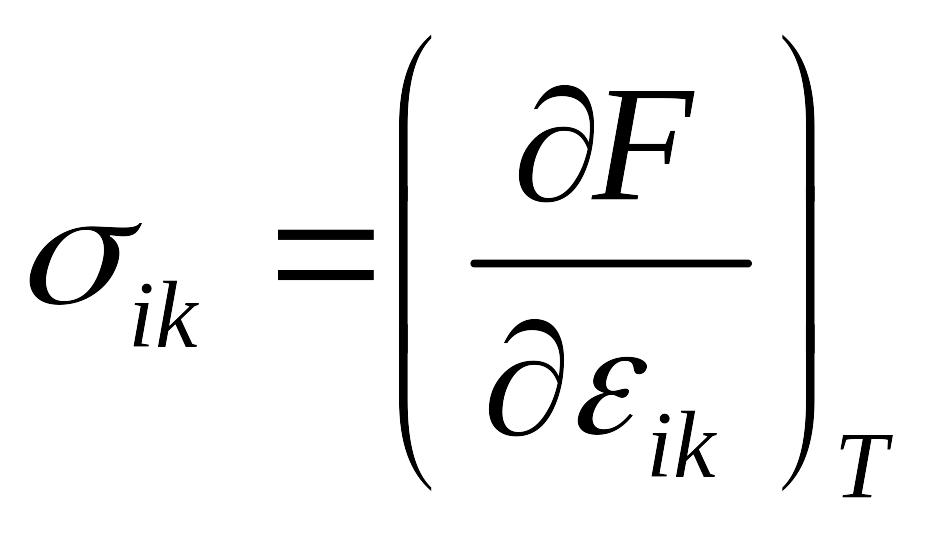и (*)

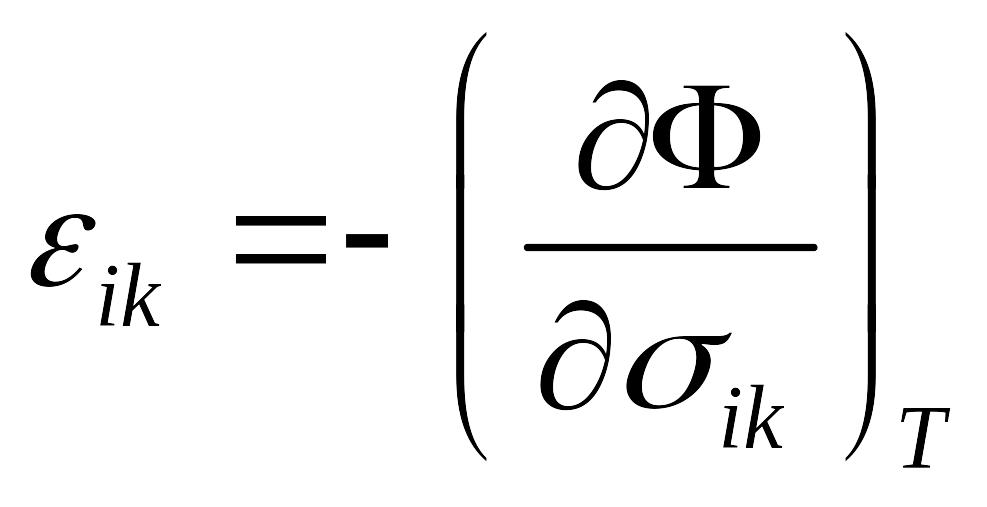В линейной теории упругости для изотермических процессов величины и могут быть представлены в виде квадратичных форм:

(**),

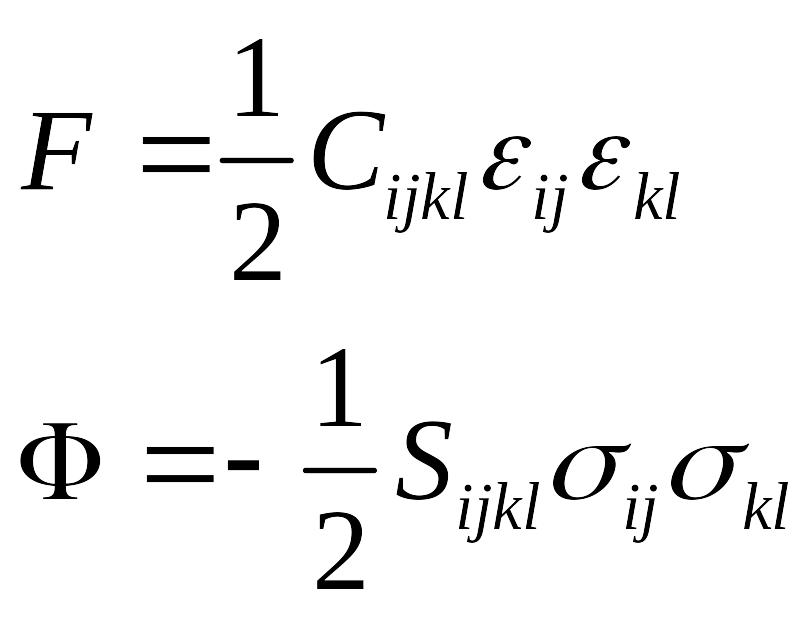где - тензор модулей упругости, - тензор податливостей.

Здесь в недеформированном состоянии . Подставляя (**) в (*) получаем:

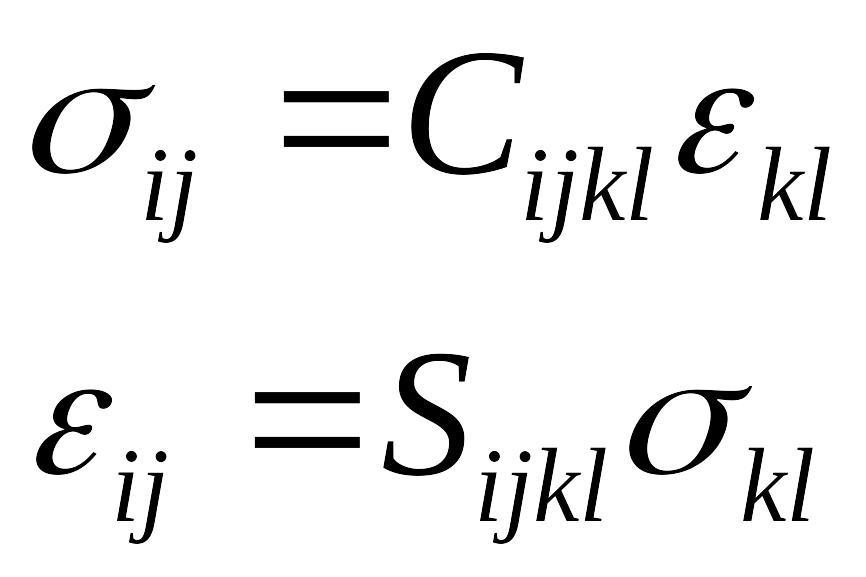- обобщенный закон Гука для анизотропных материалов в тензорной форме

Из этих выражение можно получить связь тензоров модулей упругости и податливости . В компонентах:

,

где - единичный тензор.

В общем случаем эти тензоры содержат по 81 компоненте, каждая из которых характеризует упругие свойства тела вдоль определенного направления.

Однако, из-за симметрии физического мира:

,

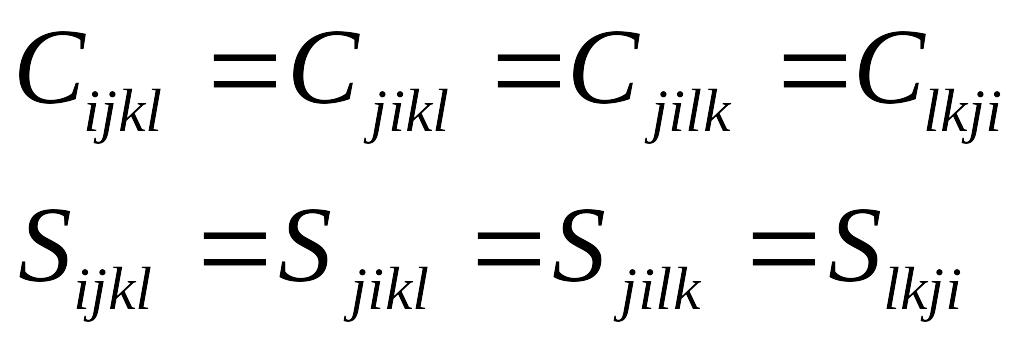что позволяет снизить количество независимых компонентов до 21.

Наряду с тензорной формой записи обобщенного закона Гука используется его матричная запись:

,

где . Для матричной формы имеется симметрия:

При использовании матричной формы записи всегда принимается, что оси ортогональной декартовой системы координат согласованы с кристаллографическими осями. Переход от тензорной к матричной форме записи осуществляется объединением двух индексов в один по правилу:

Тензорное обозначение: 11 22 33 23,32 31,13 12,21

Матричное обозначение: 1 2 3 4 5 6

Обычно используют в качестве деформаций сдвига – техническую деформацию, представляющую собой тангенс угла сдвига. Поэтому деформация при в два раза больше, чем соответствующая величина :

, где m=

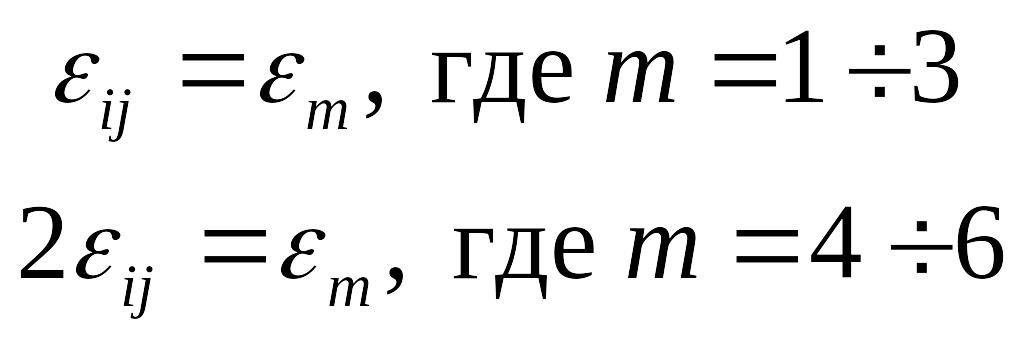
При переходе к матричному описанию :

При переходе к матричному описанию :

Е сли учитывать симметрию кристалла, отнесенного к определенному кристаллографическому классу, то число независимых коэффициентов можно ещё уменьшить. Например, для кубической сингонии имеется 3 независимые компоненты тензора четвертого ранга. Матрицы и имеют в этом случае вид:

оотношения между коэффициентами матриц и для кубической сингонии:

§2.5 Тензор модулей упругости изотропной среды.

Простейший тензор 4-го ранга – единичный тензор можно разложить на объемную и девиаторную составляющие:

,

где - объемная составляющая, а - девиаторная составляющая.

Видно, что тензоры обладают свойством, аналогичным условию ортонормированности векторных величин:

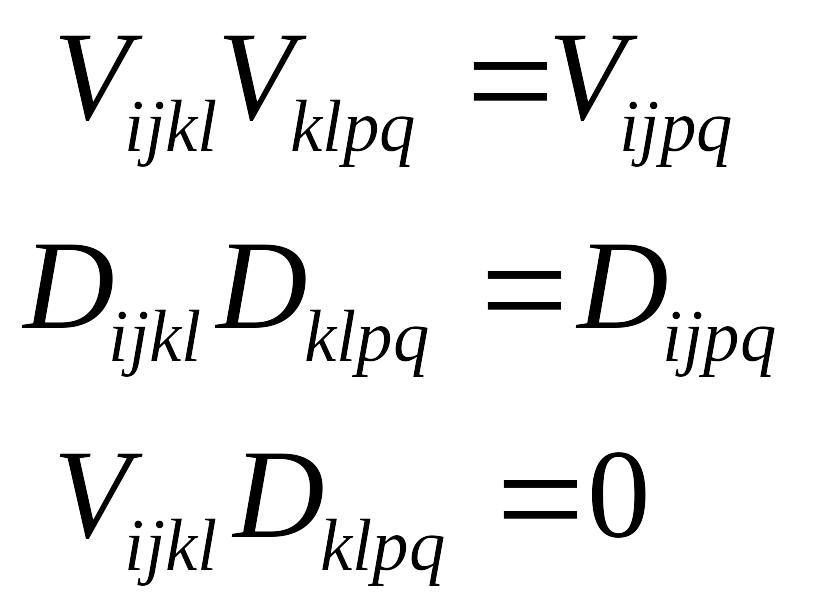
Для тензоров имеют место соотношения:

,

,

,

т.е. свертка произвольного тензора второго ранга с единичным тензором четвертого ранга оставляет его неизменным. При помощи тензоров и можно разложить тензор второго ранга на объемную и девиаторную составляющие.

Используем представление единичного тензора в виде объемной и девиаторной составляющих для представления тензоров модулей упругости и податливостей изотропной среды в виде:

,

,

где - объемный, а - сдвиговой модули упругости.

Иногда удобна такая запись:

,

где - постоянная Ламэ.

Податливости выражаются через модули объемной и сдвиговой упругости:

и

По известным модулям упругости могут быть вычислены другие постоянные упругости, например:

модуль Юнга ,

коэффициент Пуассона

Связь между постоянными упругости и модулями и изотропной среды имеет вид:

Формулы, выражающие объемный и сдвиговой модули упругости через тензорные свертки величин и :

,

,

Эти соотношения могут быть использованы для вычисления средних модулей упругости поликристаллов.