§ 1.5 Задача о брахистохроне.

Исследовать на экстремум функционал

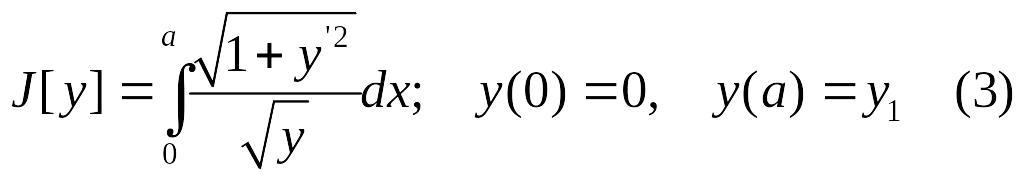
Решение. Подынтегральная функция не зависит явно от х, следователь получаем , или в нашем случае

откуда

где

Положим . Будем иметь .

Далее,

Интегрируя, получим

Итак,

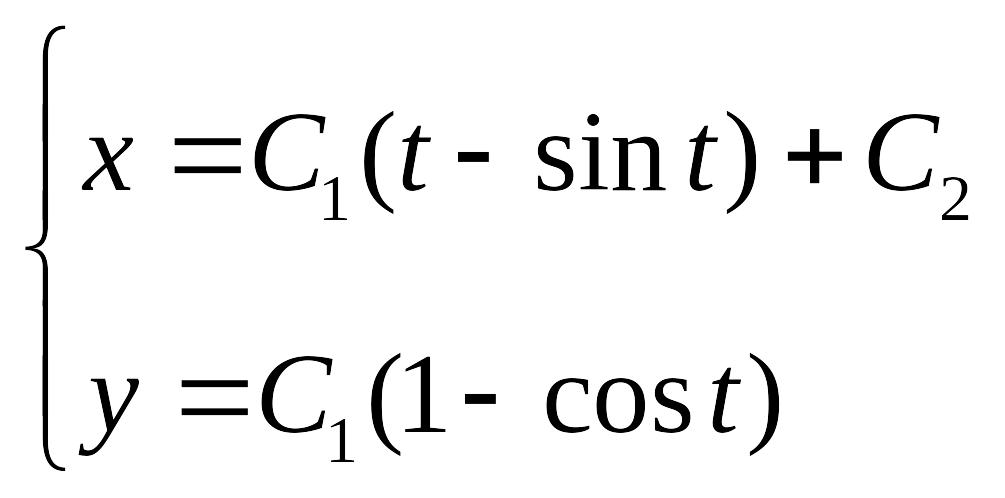
—параметрические уравнения семейства циклоид. Из условия у(0) = 0 находим, что

С₂ = 0. Пучок циклоид

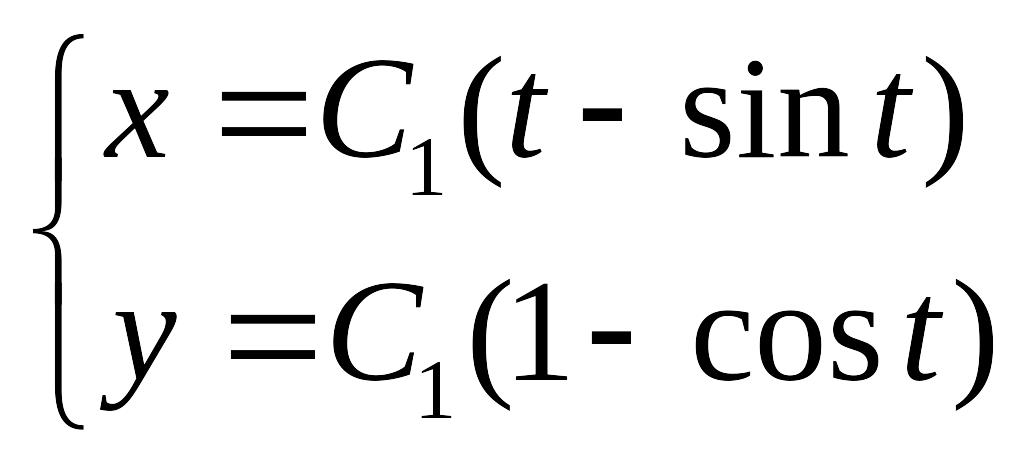
образует центральное поле с центром в точке O(0,0), включающее экстремаль

где R определено из условия прохождения циклоида через вторую граничную точку B(a,y₁), если а < 2πR (рис. 13).

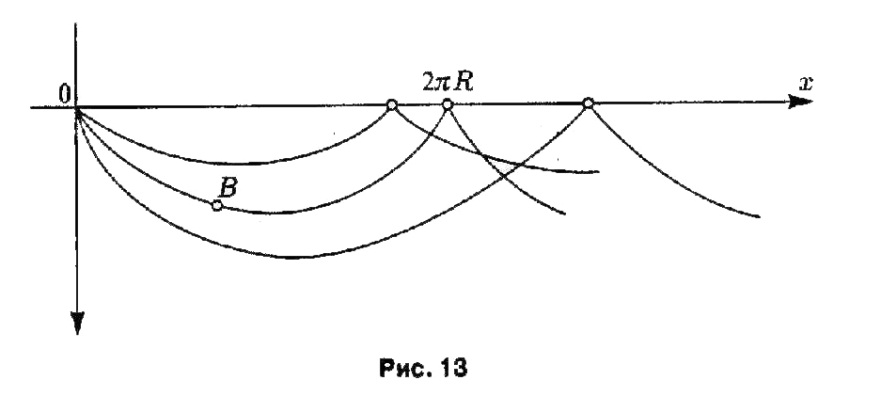
Используем условие Лежандра. Имеем

при любых значениях у'. Значит, для а < 2πR на циклоиде

данный функционал имеет сильный минимум.

Приведем графическое пояснение к решению данной задачи:

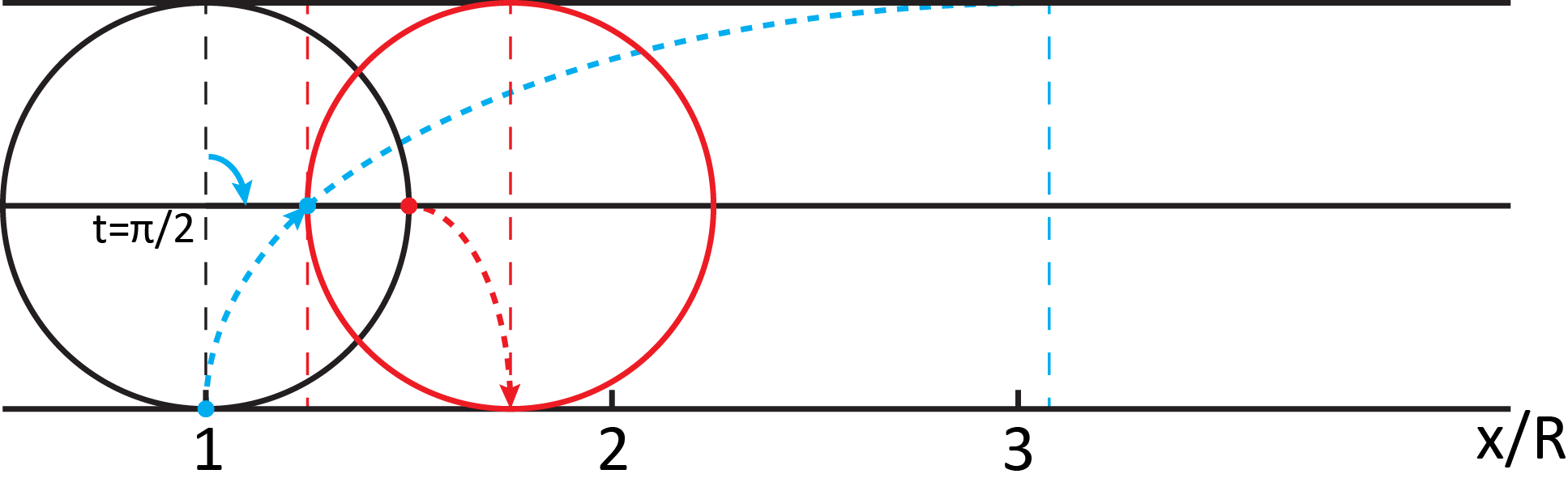
Рисунок 6.1. Движение циклоиды.

При , получаем

,

.

При , получаем

,

.

Это видно из рисунка 6.1, приведенного выше, на котором изображено движение циклоиды.

Задача о брахиcтохроне, непосредственно связанная с функционалом (3), была сформулирована в 1696 г. Бернулли. Она сильно способствовала развитию вариационных методов.

Задача состоит в отыскании траектории быстрейшего ската материальной точки под действием силы тяжести между двумя заданными точками А и В, не лежащими на одной вертикальной прямой. Выберем декартову систему координат так, чтобы точки А и В имели координаты (0,0) и (a, y₁|), соответственно (рис.14).

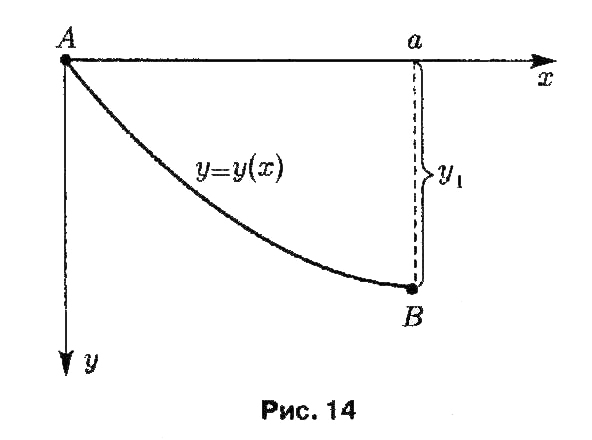
Скорость точки v в зависимости от ординаты у, выражается по формуле где g - ускорение свободного падения. Пусть у = у(х) — искомая траектория точки, а ds — элемент дуги.

Тогда , откуда и

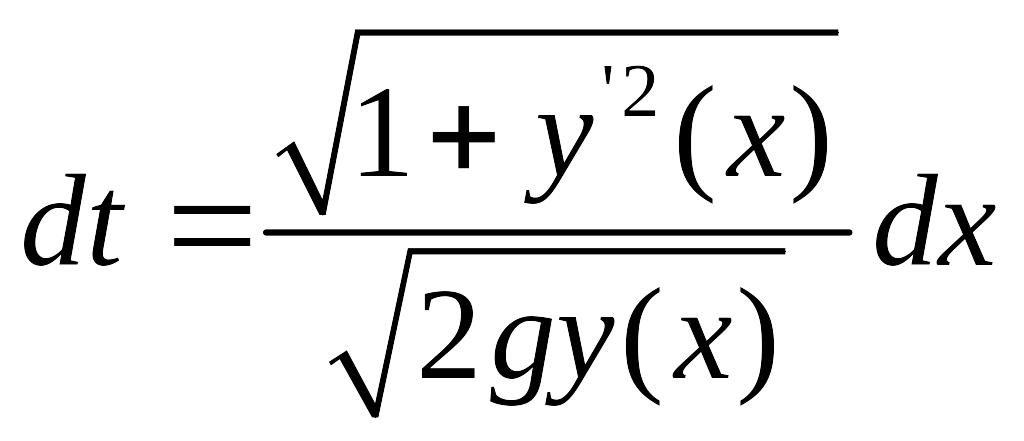
Интегрируя по x в пределах от х = 0 до х = а, получаем время затрачиваемое точкой на перемещение из А в В по траектории у(х)

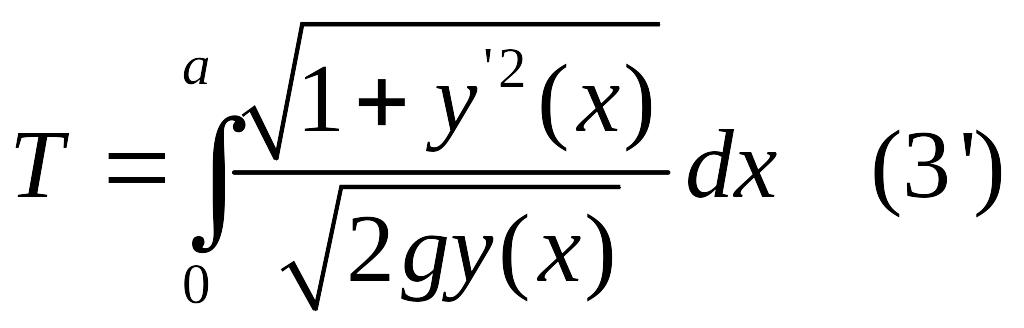
Таким образом, задача сводится к нахождению минимума функционала (3'), который отличается от (3) только на числовой множитель. Следовательно, брахистохрона доставляет минимум функционалу (3), т.к.является циклоидой из семейства, определенного выше.

§ 1.6 Задача Дидоны.

Среди замкнутых кривых длины 2l найти ту, которая ограничивает наибольшую площадь.

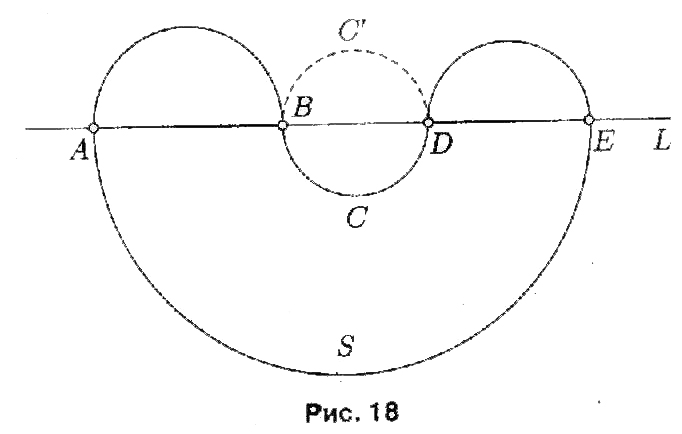
Решение. Заметим прежде всего, что рассматриваемая кривая должна быть выпуклой. В самом деле, в противном случае существовала бы прямая L (рис. 18) такая, что если зеркально отразить в ней кусок границы BCD, то мы бы получили область большей площади, чем первоначальная, при той же длине границы.

Далее заметим, что всякая прямая, которая делит пополам замкнутую кривую, ограничивающую наибольшую площадь, будет делить пополам и саму эту площадь. В самом деле, допустим противное и пусть прямая L₁ не обладает этим свойством. Отразив тогда зеркально около L₁, ту часть фигуры, которая имеет большую площадь, мы получили бы кривую той же длины, но ограничивающую большую площадь.

Выбирая за ось Ох любую из прямых, делящих кривую пополам, приходим к следующей постановке задачи.

Найти линию , которая при заданной длине I > 2а ограничивает вместе с отрезком оси Ох наибольшую площадь. Таким образом, задача свелась к разысканию экстремума функционала

,

при дополнительном условии, что

Составляем вспомогательную функцию

и рассматриваем вспомогательный функционал

Уравнение Эйлера для функционала (2) имеет вид

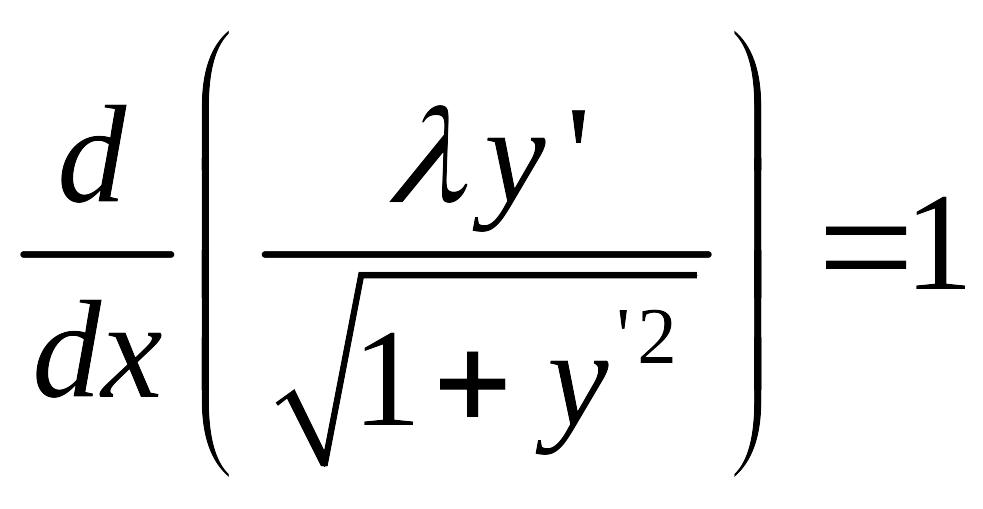
откуда

Решая последнее уравнение относительно у', находим

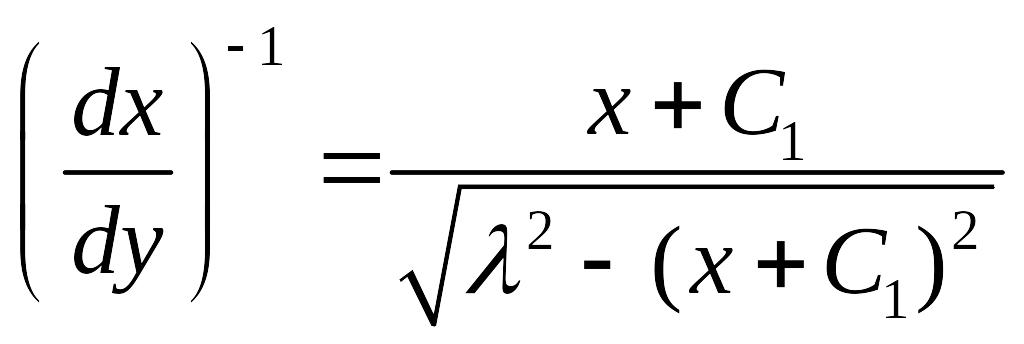
Интегрируя уравнение (3), получим

— окружность радиуса λ с центром в точке (-С₁,-С₂). Постоянные С₁,-С₂ и параметр λ определяем из граничных условий и изопериметрического условия (1). Имеем

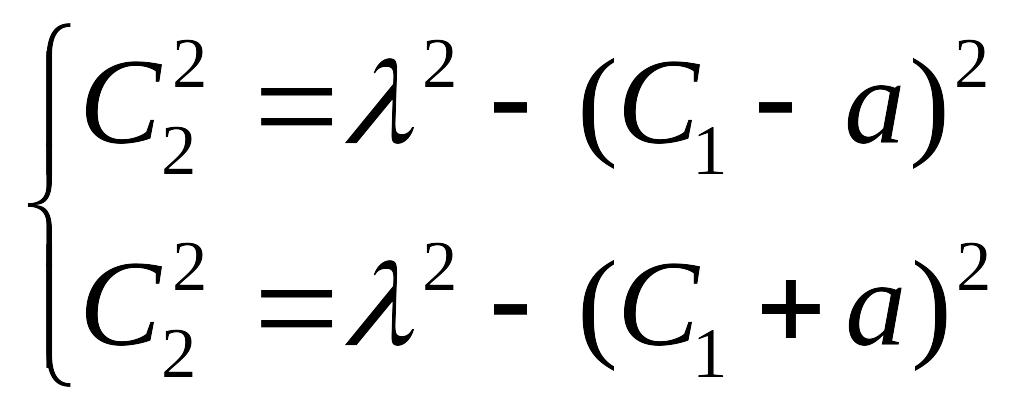
Откуда

так что

Тогда условие (1) дает

или

Решая это трансцендентное относительно λ уравнение, находим некоторое значение λ = λ₀, а затем находим величину

Нетрудно заметить, что уравнение всегда имеет решение. Действительно, полагая , сведем это уравнение к виду , где в силу условия задачи . Функция имеет в точке t = 0 наклон касательной , а функция у = at имеет меньший наклон. Следовательно, графики этих функций имеют, кроме точки O(0,0), еще по крайней мере одну точку пересечения.

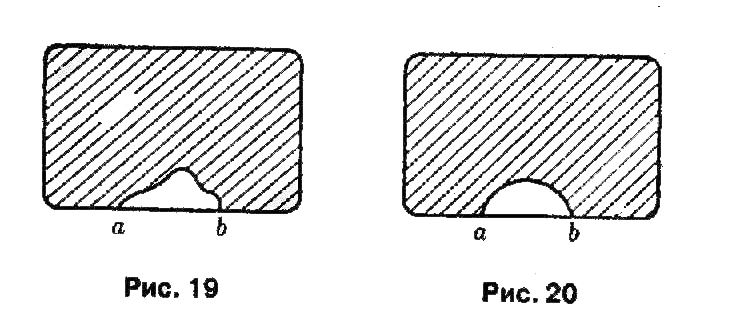
Задача Дидоны тесно связана с другим известным явлением, которое можно легко проверить на практике. На поверхности тонкой мыльной пленки плавает нить, концы которой а и b закреплены на контуре, на который натянута пленка (рис. 19). Если проткнуть пленку с любой стороны от нити, то нить примет форму полуокружности, при этом площадь пленки сократиться до минимально возможного значения (рис.20).