§ 1.3 Функционалы вида

Для получения необходимых условий экстремума функционала более общего вида

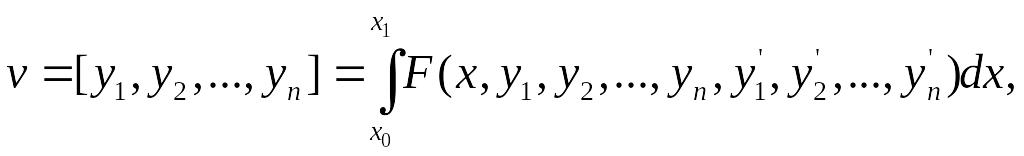
при заданных граничных значениях всех функций

будем варьировать лишь одну из функций

оставляя все остальные функции неизменными. При этом функционал превратится в функционал, зависящий лишь от одной варьируемой функции, например от ,

рассмотренного в § 2 вида, и, следовательно, функция, реализующая экстремум, должна удовлетворять уравнению Эйлера

Так как это рассуждение применимо к любой функции то мы получим систему дифференциальных уравнений второго порядка

определяющих, вообще говоря, 2n-параметрическое семейство интегральных кривых в пространстве — семейство экстремалей данной вариационной задачи.

Если, в частности, функционал зависит лишь от двух функций

у(х) и z(x):

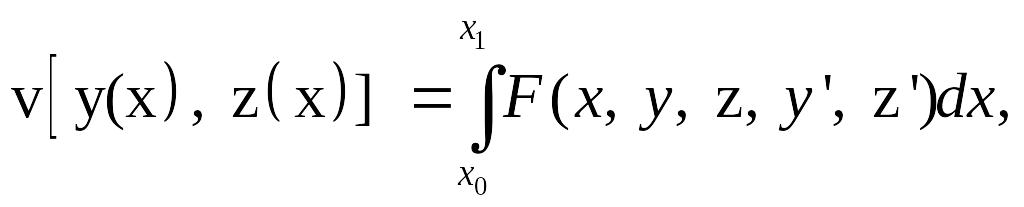
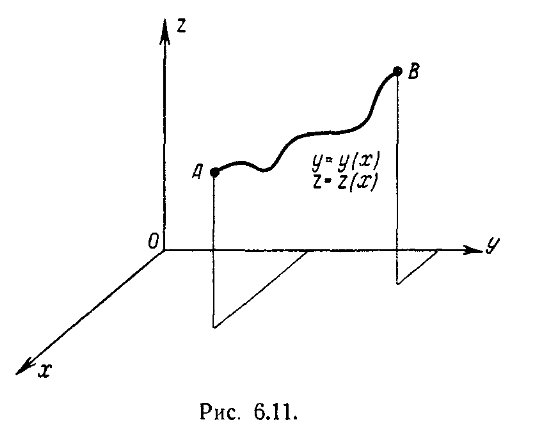
т. е. определяется выбором пространственной кривой (рис. 6.11), то, варьируя только и фиксируя , Рис. 6.11.

мы изменяем нашу кривую так, что ее проекция на плоскости не изменяется, т. е. кривая все время остается на проектирующем цилиндре (рис. 6.12).

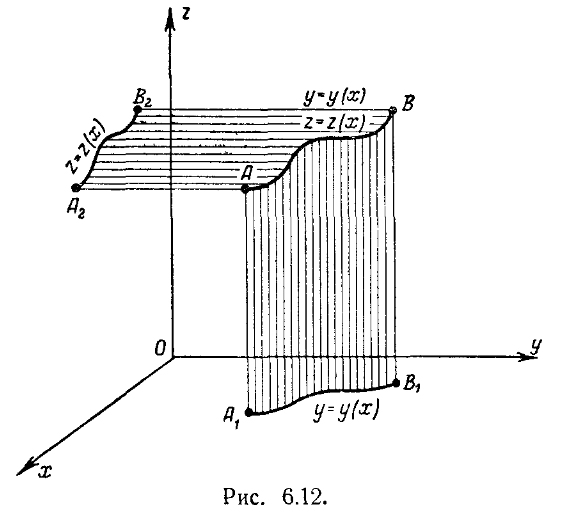
Аналогично, фиксируя и варьируя , мы варьируем кривую так, что она все время лежит на проектирующем цилиндре При этом получаем систему двух уравнений Эйлера:

.

Пример 1. Найти экстремали функционала

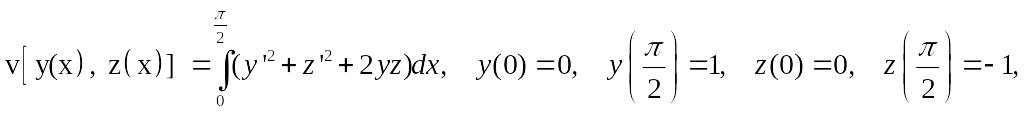
Система дифференциальных уравнений Эйлера имеет вид

Исключая одну из неизвестных функций, например z, получаем

Интегрируя это линейное уравнение с постоянными коэффициентами, будем

иметь;

Используя граничные условия, находим:

следовательно, .

Пример 2. Найти экстремали функционала

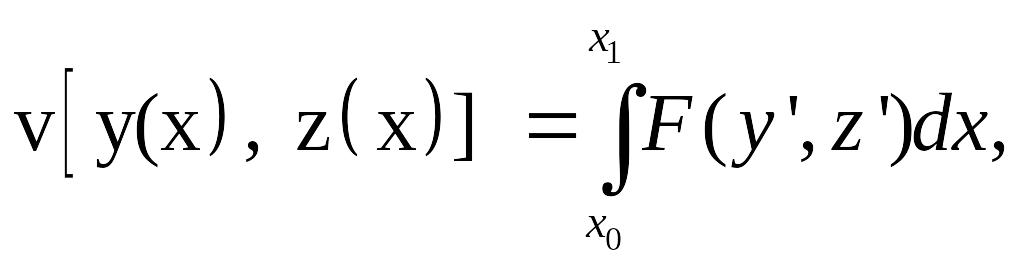
Система уравнений Эйлера имеет вид

откуда, считая, получим: и или — семейство прямых линий в пространстве.

Пример 3. Найти дифференциальные уравнения линий распространения света в оптически неоднородной среде, в которой скорость распространения света равна .

Согласно принципу Ферми свет распространяется из одной точки в другую пo кривой, для которой время Т прохождения света будет наименьшим. Если уравнение искомой кривой , то

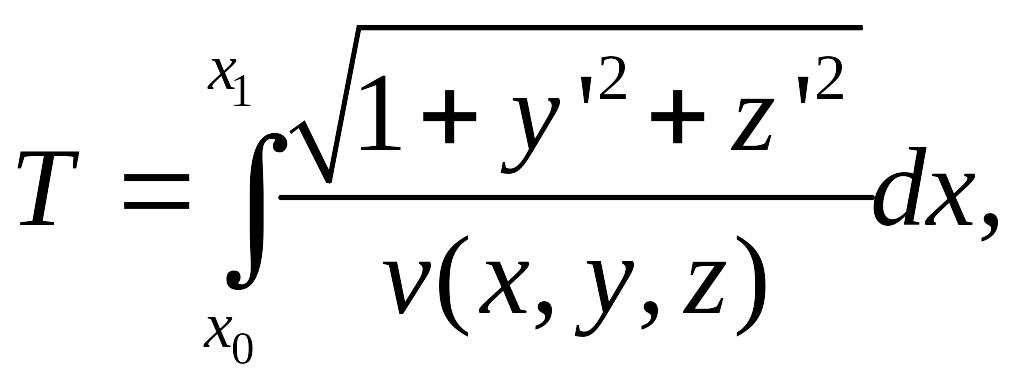
Система уравнений Эйлера для этого функционала

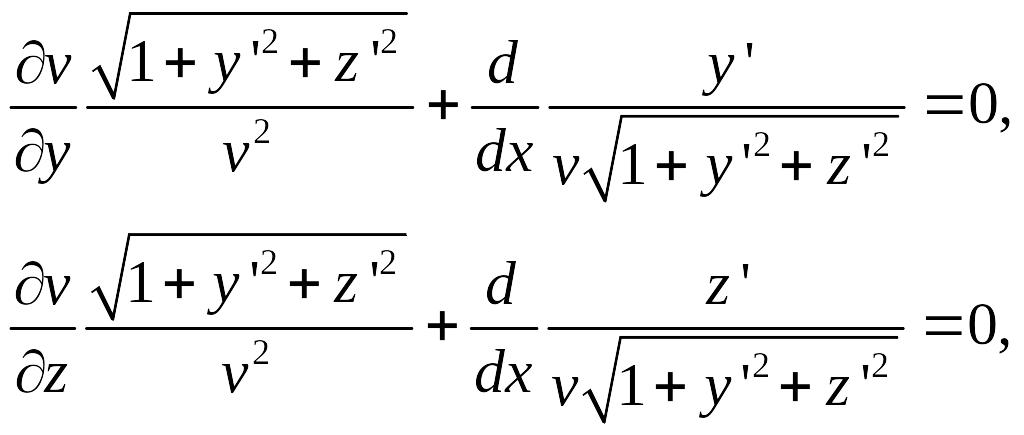
и будет системой, определяющей линии распространения света.

§ 1.4 Функционалы, зависящие от производных более высокого порядка

Исследуем на экстремум функционал

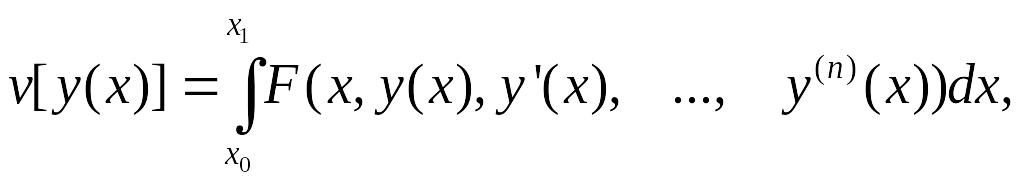
где функцию F будем считать дифференцируемой n+2 раза по всем аргументам и будем предполагать, что граничные условия имеют вид

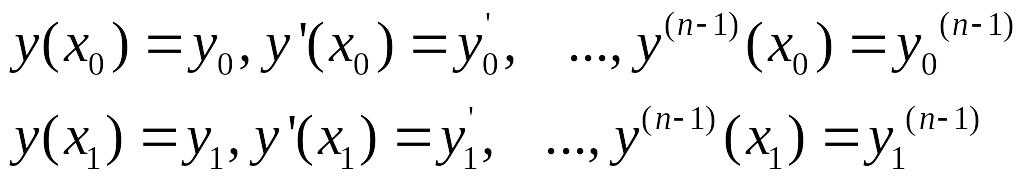
т. е. в граничных точках заданы значения не только функции, но и ее, производных до порядка n-1 включительно. Предположим, что экстремум достигается на кривой у = у(х), дифференцируемой 2n раз, и пусть — уравнение некоторой кривой сравнения, также дифференцируемой 2n раз.

Рассмотрим однопараметрическое семейство функций

При α = 0 у(х, a) = y(x), при α =1 у(х, a) = Если рассматривать значение функционала только на кривых семейства , то функционал превратится в функцию параметра , достигающую экстремума при а = 0; следовательно,

. Эта производная в соответствии с § 1 называется вариацией функционала v и обозначается ;

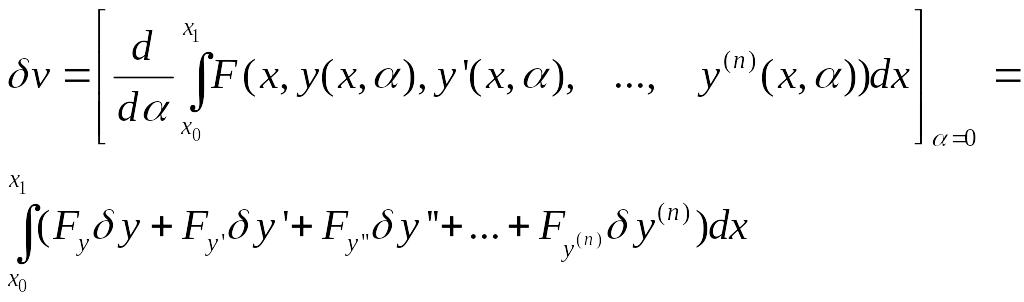
Интегрируем по частям второе слагаемое в правой части один раз:

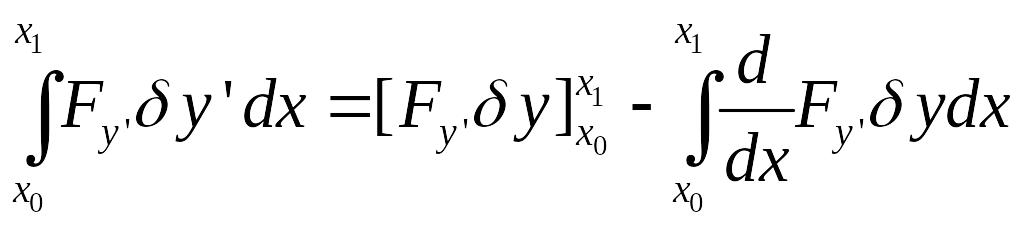
третье слагаемое — два раза:

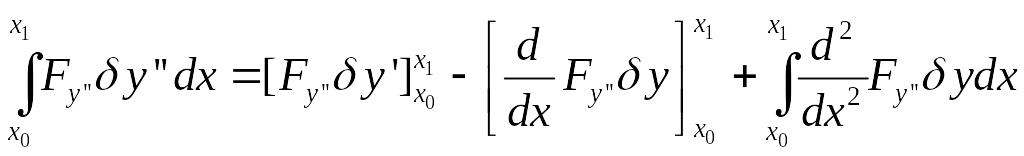
и т. д., последнее слагаемое - n раз:

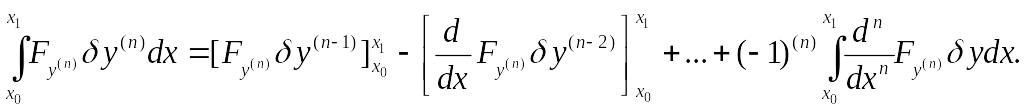
Принимая во внимание граничные условия, в силу которых при

х = х₀ и при х = х₁ вариации δу = δу' = δу" = ... =δy^(n-1)=0,

окончательно получим

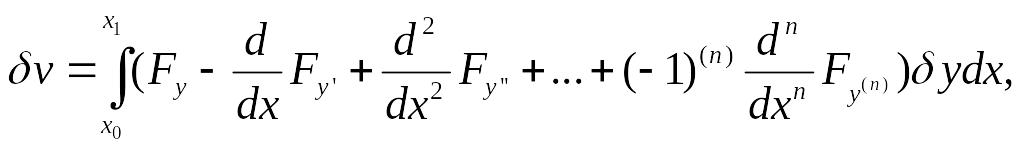
Так как на кривой, реализующей экстремум, имеем

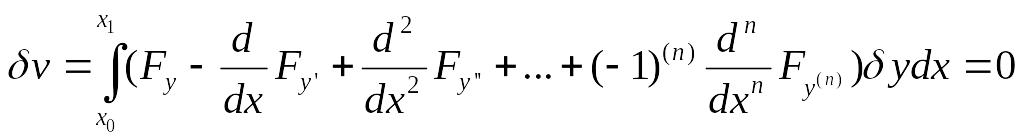
при произвольном выборе функции δу и так как первый множитель под знаком интеграла является непрерывной функцией х на той же кривой у = у (х), то в силу основной леммы первый множитель тождественно равен нулю:

Итак, функция у = у(х), реализующая экстремум функционала

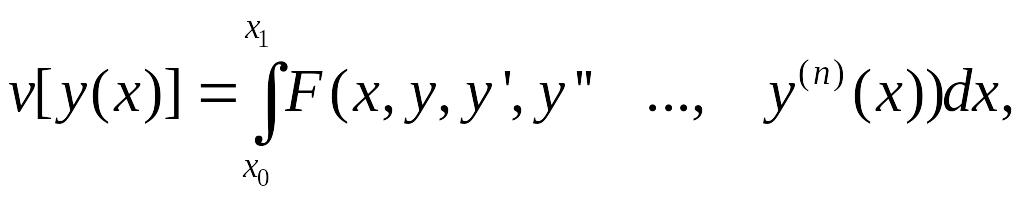
должна быть решением уравнения

Это дифференциальное уравнение порядка 2n носит название уравнения Эйлера—Пуассона, а его интегральные кривые называются экстремалями рассматриваемой вариационной задачи. Общее решение этого уравнения содержит 2n произвольных постоянных, которые могут быть, вообще говоря, определены из 2n граничных условий:

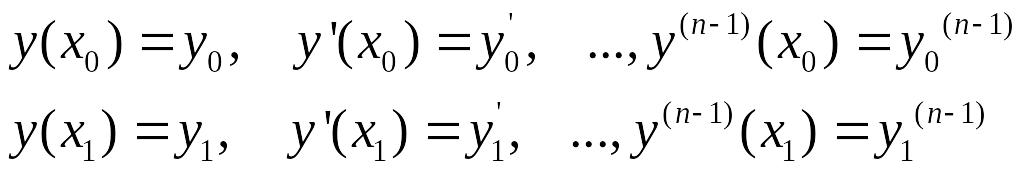
Пример 1. Найти экстремаль функционала

Уравнение Эйлера — Пуассона имеет вид или y^IV = 0;ero

общим решением является . Используя граничные условия, получаем:

Итак, экстремум может достигаться лишь на прямой у = х.

Пример 2. Определить экстремаль функционала

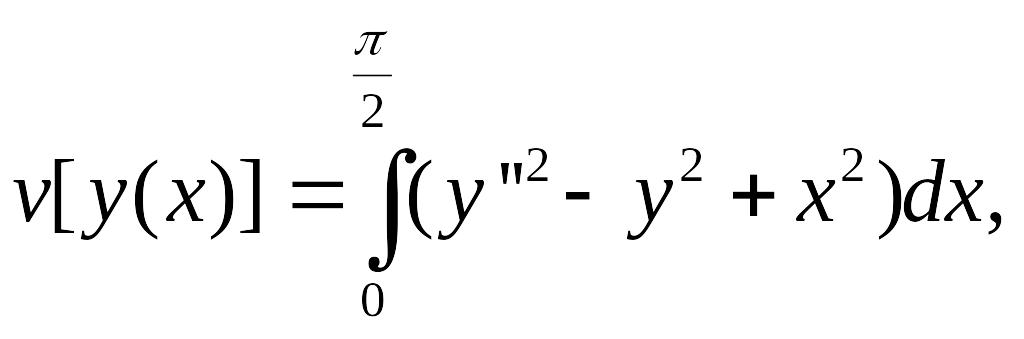
удовлетворяющую условиям

Уравнение Эйлера - Пуассона имеет вид его общим решением является . Используя граничные условия, получаем . Итак, экстремум может достигаться лишь на кривой у = cos x.

Пример 3. Определить экстремаль функционала

удовлетворяющую граничным условиям:

К этой вариационной задаче сводится нахождение оси изогнутой упругой цилиндрической балки, заделанной на концах. Если балка однородна, то ρ и μ постоянны и уравнение Эйлера — Пуассона имеет вид

откуда

Используя граничные условия, окончательно находим

Если функционал v имеет вид

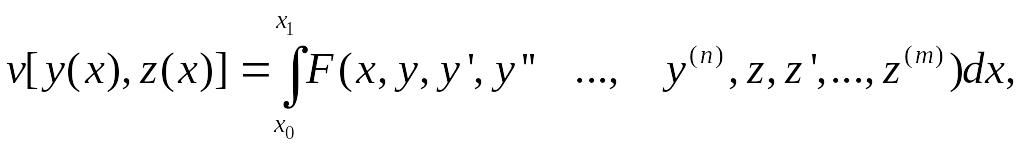
то, варьируя только у(х) и считая z (x) фиксированным, мы находим, что функции у(х) и z(x), реализующие экстремум, должны удовлетворять уравнению Эйлера — Пуассона,

а варьируя z(x) и считая у(х) фиксированным, получим, что те же функции должны удовлетворять уравнению

Итак, функции z (x) и у (х) должны удовлетворять системе двух уравнений

Точно так же можно рассуждать и при исследовании на экстремум функционала, зависящего от любого числа функций:

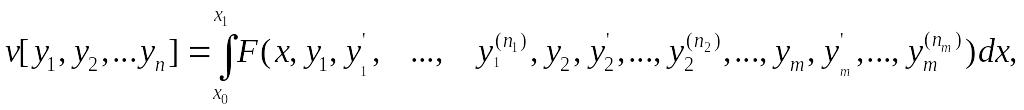
Варьируя какую-нибудь одну функцию y_i (x) и сохраняя остальные неизменными, получим основное необходимое условие экстремума в виде