§ 1.2 Уравнение Эйлера.

И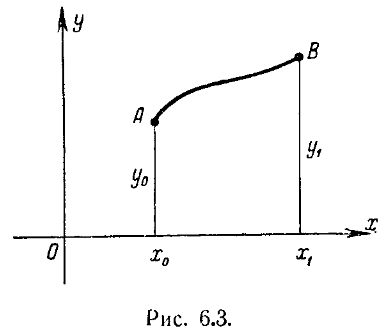 сследуем на экстремум функционал

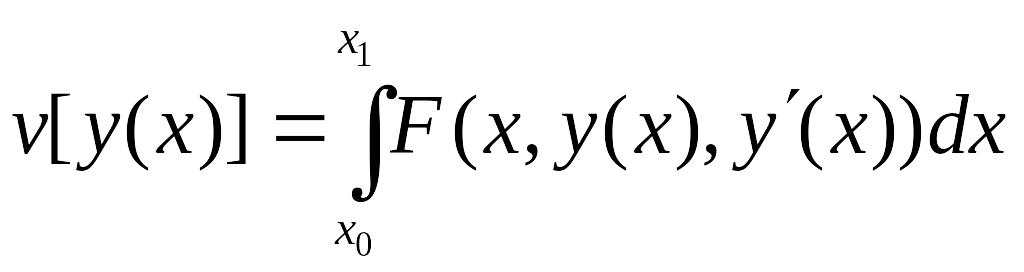(1)

причем граничные точки допустимых кривых закреплены: и (рис. 6.3). Функцию F(x, у, у') будем считать трижды дифференцируемой.

Мы уже знаем, что необходимым условием экстремума является обращение в нуль вариации функционала. Покажем теперь, как применяется эта основная теорема к рассматриваемому функционалу, причем мы еще раз повторим предыдущее рассуждение применительно к функционалу (1). Предположим, что экстремум достигается на дважды дифференцируемой кривой у = у (х) (требуя лишь существования производных первого порядка у допустимых кривых, можно иным методом доказать, что у кривой, реализующей экстремум, существует и вторая производная).

Возьмем какую-нибудь близкую к допустимую кривую и включим эти кривые в однопараметрическое семейство кривых

при получим , в противном случае (рис. 6.4). Как мы уже знаем, разность называется вариацией функции у(х).

Вариация в вариационных задачах играет роль, аналогичную роли приращения независимого переменного в задачах на исследование экстремумов функций . Вариация функции является функцией х. Эту функцию можно дифференцировать один или несколько раз, причем производная вариации равна вариации производной.

Итак, рассмотрим семейство , , содержащее при кривую, на которой достигается экстремум, а при — некоторую близкую допустимую кривую — так называемую кривую сравнения.

Если рассматривать значения функционала

только на кривых семейства , то функционал превращается в функцию :

так как значение параметра определяет кривую семейства и тем самым определяет и значение функционала . Эта функция достигает своего экстремума при , так как при получаем , и функционал, по предположению, достигает экстремума по сравнению с любой близкой допустимой кривой и, в частности, по отношению к близким кривым семейства . Необходимым условием экстремума функции при , как известно, является обращение в нуль ее производной при :

Так как

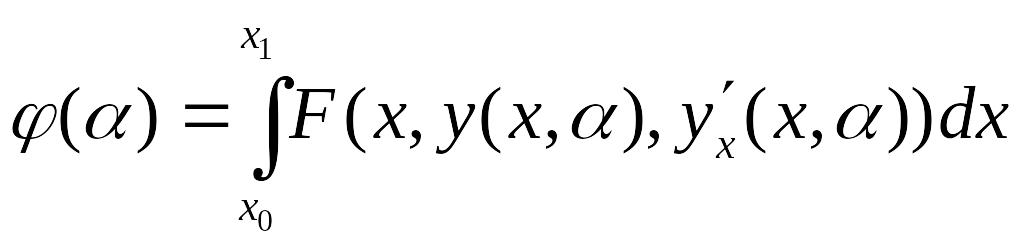
то

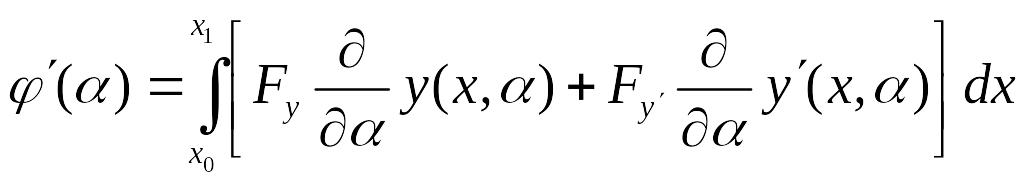
Тогда при получаем:

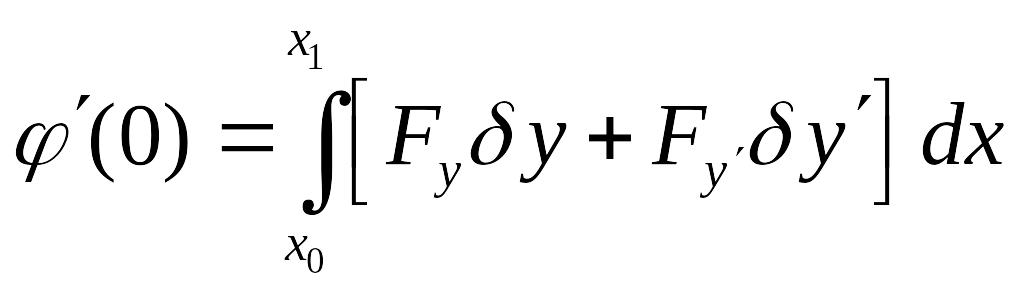
Как мы уже знаем, называется вариацией функционала и обозначается . Необходимое условие экстремума функционала заключается в обращении в нуль его вариации: . Для функционала

Это условие имеет вид:

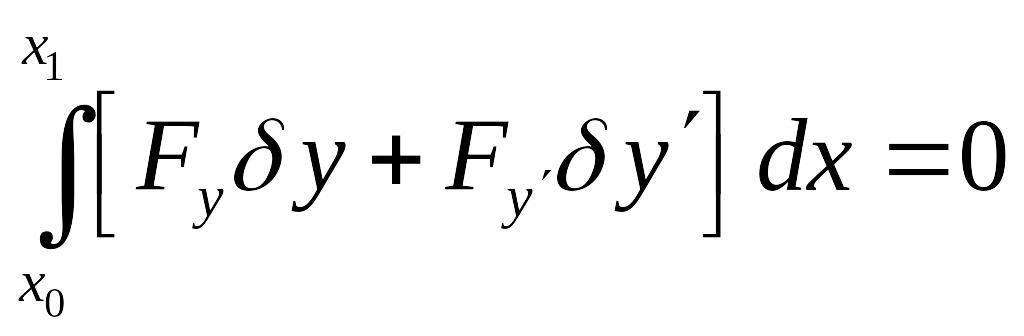
Интегрируем второе слагаемое по частям, получаем:

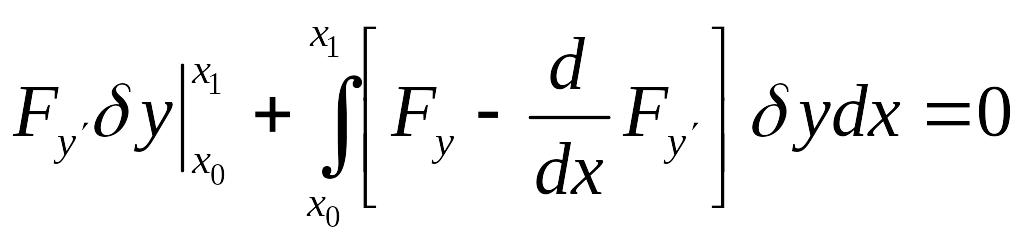
Первое слагаемое в силу того что концы закреплены обращается в нуль.

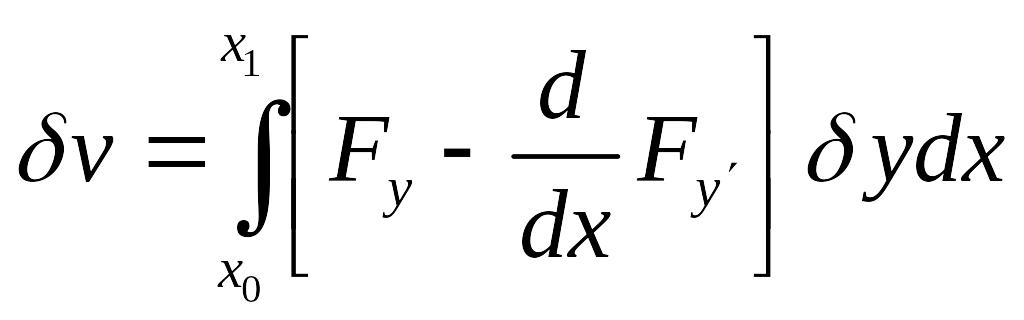
Таким образом, необходимое условие экстремума приобретает вид:

причем первый множитель на кривой , реализующей экстремум, является заданной непрерывной функцией, а второй множитель, ввиду произвола в выборе кривой сравнения, является произвольной функцией, удовлетворяющей лишь некоторым весьма общим условиям, а именно: функция в граничных точках обращается в нуль, непрерывна и дифференцируема один или несколько раз. или и малы по абсолютной величине.

Для упрощения полученного условия воспользуемся следующей леммой:

Основная лемма вариационного исчисления. Если для каждой непрерывной функции

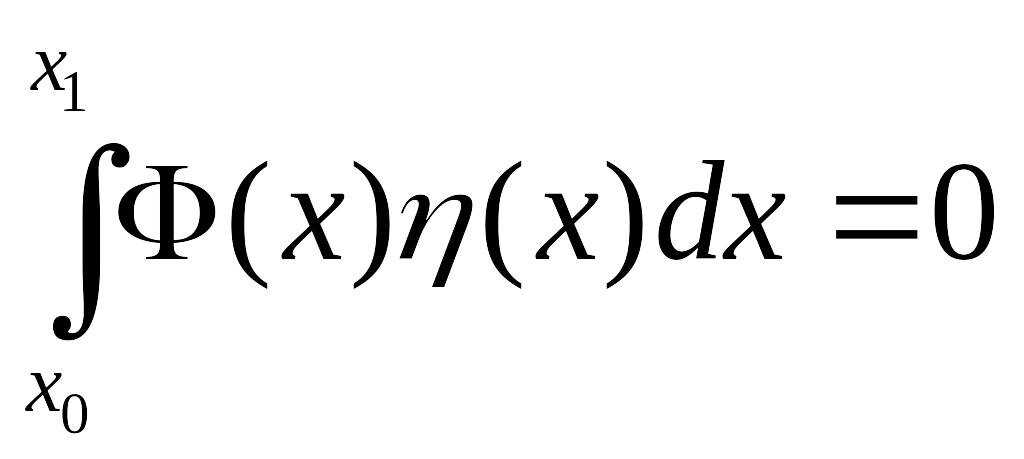
где функция Ф(х) непрерывна на отрезке , то

на том же отрезке.

Для нашего случая все условия леммы выполнены: на кривой, реализующей экстремум, множитель является непрерывной функцией, а вариация является произвольной функцией, на которую наложены лишь предусмотренные в основной лемме ограничения общего характера, следовательно, на кривой , реализующей экстремум рассматриваемого функционала, т. е. является решением дифференциального уравнения второго порядка

или в развернутом виде

Это уравнение называется уравнением Эйлера (оно впервые было им опубликовано в 1744 году). Интегральные кривые уравнения Эйлера называются экстремалями. Только на экстремалях может достигаться экстремум функционала

Для нахождения кривой, реализующей экстремум этого функционала, интегрируем уравнение Эйлера и определяем обе произвольные постоянные, входящие в общее решение этого уравнения, из условий на границе. Только на удовлетворяющих этим условиям экстремалях может реализоваться экстремум функционала. Однако для того чтобы установить, реализуется ли на них в действительности экстремум, и притом максимум или минимум, надо воспользоваться достаточными условиями экстремума.

Заметим, что во многих вариационных задачах существование решения очевидно из физического или геометрического смысла задачи, и если решение уравнения Эйлера, удовлетворяющее граничным условиям, единственно, то эта единственная экстремаль и будет решением рассматриваемой вариационной задачи.

Пример 1. На каких кривых может достигать экстремума функционал:

, ,

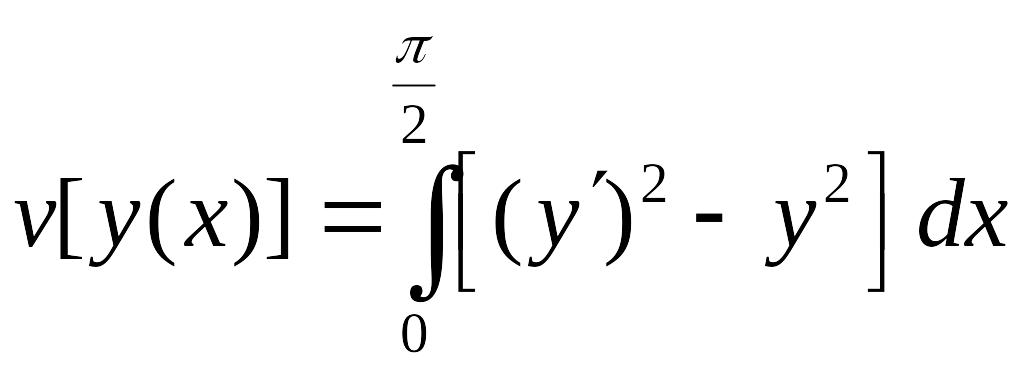Уравнение Эйлера имеет вид . Его решение, учитывая граничные условия:

Пример 2. На каких кривых может достигать экстремума функционал:

, ,

Уравнение Эйлера , решение

В этих двух примерах уравнение Эйлера легко интегрировалось, но так бывает далеко не всегда, так как дифференциальные уравнения второго порядка интегрируются в конечном виде лишь в исключительных случаях. Рассмотрим некоторые простейшие случаи интегрируемости уравнения Эйлера.

1) F зависит лишь от .

В этом случае

Пример 3. Длина дуги кривой:

имеет экстремали

Пример 4. Время, затрачиваемое на перемещение из одной точки в другую:

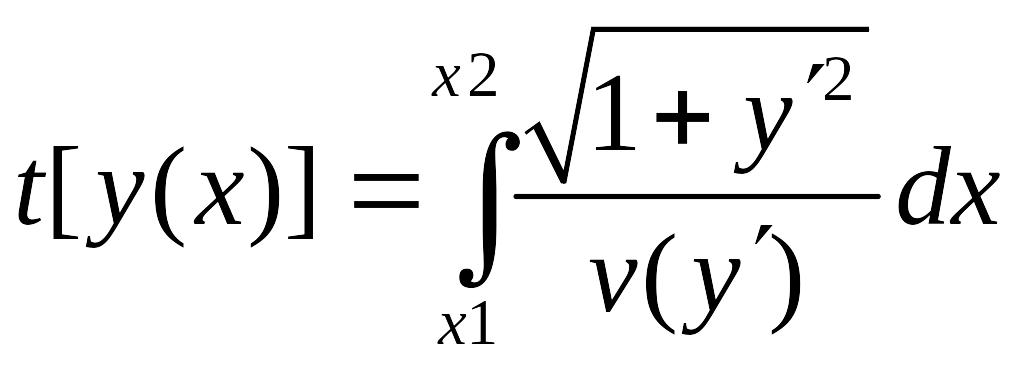
так же имеет экстремалями прямые линии.

2) F зависит лишь от x и .

Уравнение Эйлера , следовательно

3) F зависит лишь от и .

Уравнение Эйлера имеет вид . Если умножить это уравнение на , то . Следовательно, уравнение Эйлера имеет первый интеграл:

Пример 5. Задача о наименьшей поверхности вращения:

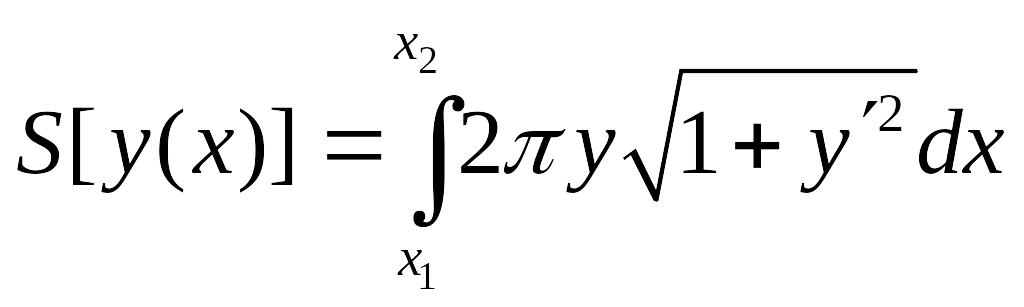
После упрощений получаем

, тогда .

После исключения параметра t будем иметь: