§13 Расчёт основных термодинамических величин фотонного газа.
Мы фактически рассмотрели излучение абсолютно чёрного тела. Электромагнитное поле описывается линейными уравнениями – уравнениями Максвелла, т.е. поля не взаимодействуют друг с другом. Поэтому фотоны между собой не взаимодействуют. А значит, газ фотонов или излучение абсолютно черного тела является идеальным бозе-газом. Но так как масса фотона равна нулю, то имеем ультрарелятивистский случай, а именно:
Но ведь
,
поэтому:
- ультрарелятивистский случай
Для фотона пишут энергию:
Так как газ ультрарелятивистский, то его уравнение состояния имеет вид:
Конечно, фотоны взаимодействуют и со средой, в которой они находятся. Здесь главное чтобы частоты наполнителя (среды) не совпадали с частотами фотонов, иначе идёт поглащение энергии излучения. В случае несовпадения частот, всё равно идет поглащение, но не столь сильное.
Рассмотрим полость (чёрное тело) в которой вакуум. Но стенки полости взаимодействуют с фотонами, т.е. идёт поглощение фотонов. Так как фотоны исчезают, то их число не сохраняется.
Так как число частиц не сохраняется, то:
даёт
- условие равновесия для фотонного газа.
Итак, для фотонов имеем и .
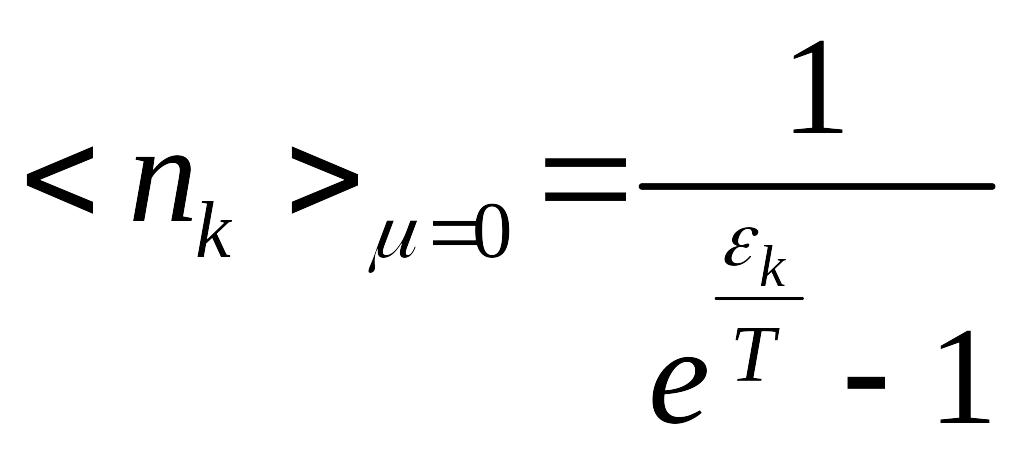
Переходим в квазиклассику:
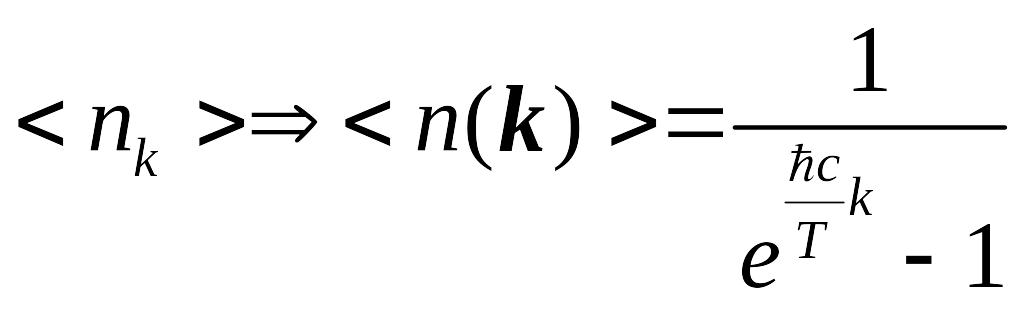
Посчитаем среднее число частиц для такого фотонного газа:
В этом выражении объём появился при интегрировании по координате.
Спин фотона равен нулю, но в данном случае:
- это член поправки. Это поправка на
поляризацию, для электромагнитных волн
– две поляризации, тогда
,
а значит:
- как для электронов, но по другой причине.
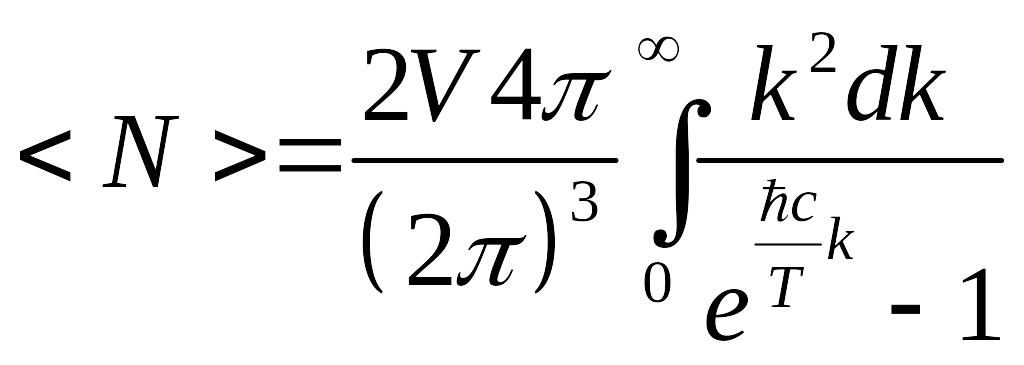
Сделаем обозначение:
,
тогда
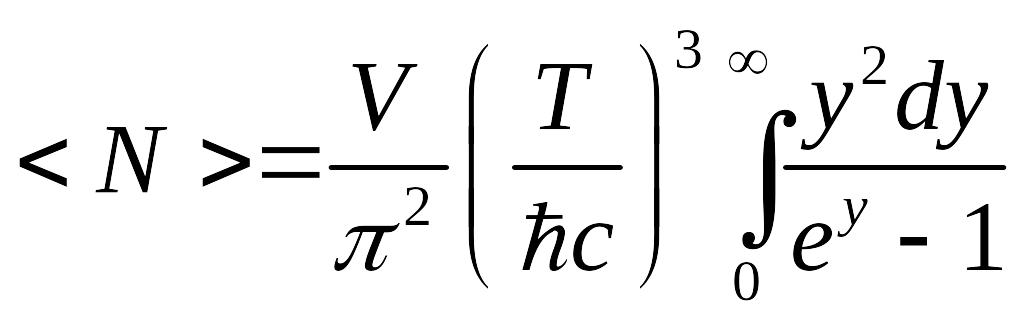
Этот интеграл можно свести к функции Римана.
,
а
Тогда:
И мы получили среднее число частиц фотонного газа.
Найдём энергию фотонного газа:
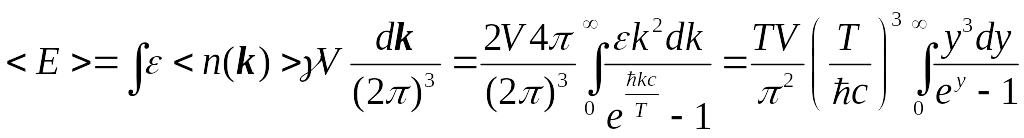
Аналогично
,
а
.
Тогда получаем:
И мы получили среднюю энергию фотонного газа. В термодинамике пишут:
Тогда:
Где
- константа Стефана-Больцмана:
- в энергетической шкале
- в градусной
- в гауссовой системе единиц.
Можно записать выражения для теплоёмкости фотонного газа:
Другие характеристики:
- для ультрарелятивистского случая
В силу того что :
,
,
§14 Метод (представление) Шредингера. Оператор эволюции и его свойства.
Существует два подхода к описанию квантово-механических систем. Согласно одному из них эволюция описывается с помощью временной зависимости волновой функции. А согласно другому – с помощью временной зависимости оператора, а волновая функция фиксирована.
В классической механике движение
системы описывается движением фазовой
точки по фазовой траектории. В классической
механике существует понятие канонического
преобразования переменных: мы можем не
говорить конкретно о динамическом
импульсе
и динамической координате
,
т. к. существует каноническое преобразование
от одних координат к другим
Движение материальной точки можно описывать с помощью канонического преобразования от координат в начальный момент времени к координатам в конечный момент времени. Т. е. эволюция классической системы может быть описана с помощью канонического преобразования.
Мы имеем уравнение Шредингера
.
Оно позволяет найти волновую функцию, описывающую эволюцию системы.
.
Но существует и
,
где
- начальный момент времени.
Существует преобразование, которое описывает эволюцию системы:
. (*)
Зная оператор
можем перейти из начального состояния
в конечное.
Подставим (*) в уравнение Шредингера
Отметим, что
- неявно зависит от динамических координат
Далее переносим все в одну часть и выносим волновую функцию за скобки
Более сложный случай, когда оператор
зависит от времени, т. е. внешнее поле
нестационарное. Уравнение (33.1) просто
решить не удается.
Будем рассматривать случай стационарного поля, когда
Для этого случая оператор имеет вид:
Мы рассматриваем способ описания
Шредингера, в котором временная
зависимость заключена в
-функцию.
Эту зависимость можно перенести на
оператор эволюции
и свести нахождение
-функции
на нахождение оператора
.
В большинстве случаев операторы явно не зависят от времени.
.
Тогда возникает ситуация, когда зависит от времени. Тогда вся информация об эволюции заключена в функции или в операторе эволюции.
Свойства оператора эволюции:
Он удовлетворяет уравнению
,
при
,
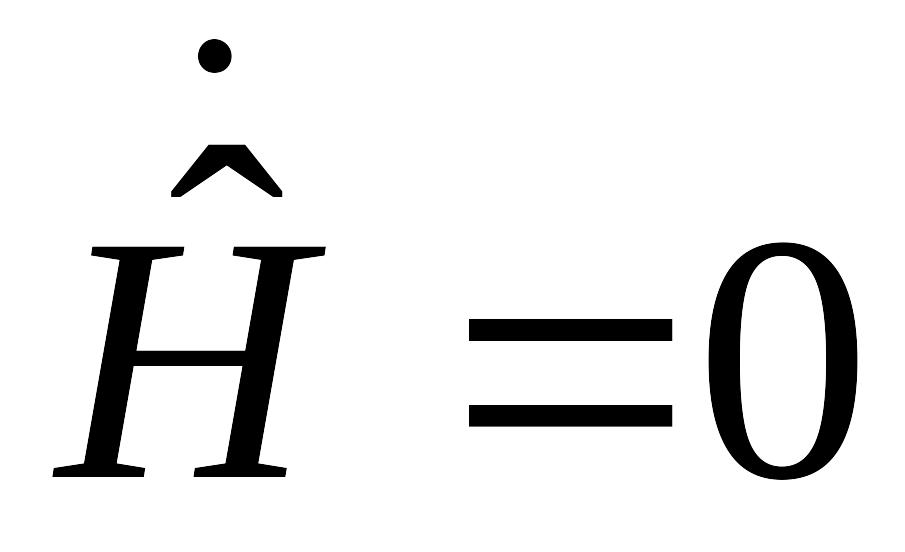- унитарный оператор.
Докажем это
Уравнение обеспечивает сохранение нормы, т.е.
.
Норму можно взять в любой момент времени.
Подставим в условие нормировки уравнение
(1), причем положим
,
тогда
.
Таким образом
,
- унитарный оператор.