§10 Многомерное Гауссово распределение.
Мы получили:
Теперь следует получить константу. Если записать матрицу в главных осях, то она диагонализируется, формула (36) упрощается.
Запишем новые переменные:
,
где
- это матрица преобразования координат.
Тогда получаем:
(37)
Легко видеть, что
Рассмотрим
:
Имеем условие нормировки
Из него и находим константу
.
Имеем
У Ландау записано
.
Можем записать аналогично:
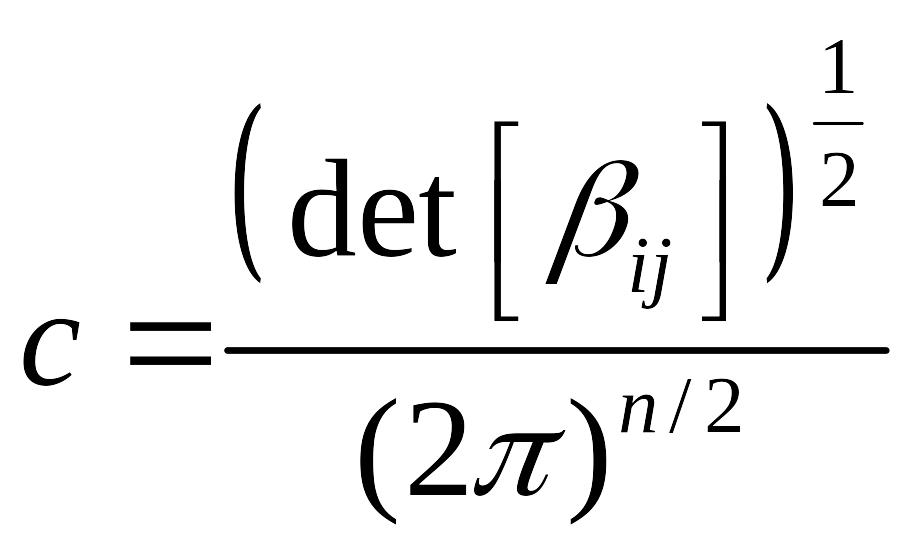
Ланаду понимает под
определитель
.
Рассмотрим термодинамически сопряженные величины, которые вообдятся соотношением:
Можно найти такие средние:
- это как смешанные моменты
У Ландау записан результат для частного случая:
Хотя результат можно получить несколько иначе. Запишем среднее:
(*)
Продефференцируем равенство (*):
Мы знаем, что:
Тогда:
В результате имеем:
Тогда имеем:
и можем автоматически дописывать
:
Теперь если заменить
на
,
тогда получим:
Если слева и справа умножить это выражение на матрицу, обратную к , то получим:
т.е. матрица, обратная к есть матрица дисперсий, или матрица ковариаций.
§11 Расчёт флуктуаций термодинамических величин.
В качестве примера рассмотрим такую функцию:
Если записать первое начало термодинамики, то будем иметь:
Пусть
,
а
,
тогда:
и
Теперь найдём :
- это коэффициент объёмного расширения
- коэффициент сжимаемости
Например, для идеального газа:
,
тогда
Итак, мы нашли все элементы матрицы .
Найдём теперь
и
:
Перепишем последнее выражение немножко иначе:
Аналогично пишется для
:
Учтём, что , тогда:
§12 Расчет термодинамических величин вырожденного Бозе-газа.
Рассчитаем энергию вырожденного Бозе-газа:
- это переходит в интеграл в квазиклассическом
приближении:
здесь свободно переходим в квазиклассику, т.к. здесь на нулевом уровне .
,
- это средняя энергия одной частицы.
т.е. усреднение энергии сводится к
усреднению
Поделим
на
,
тогда:
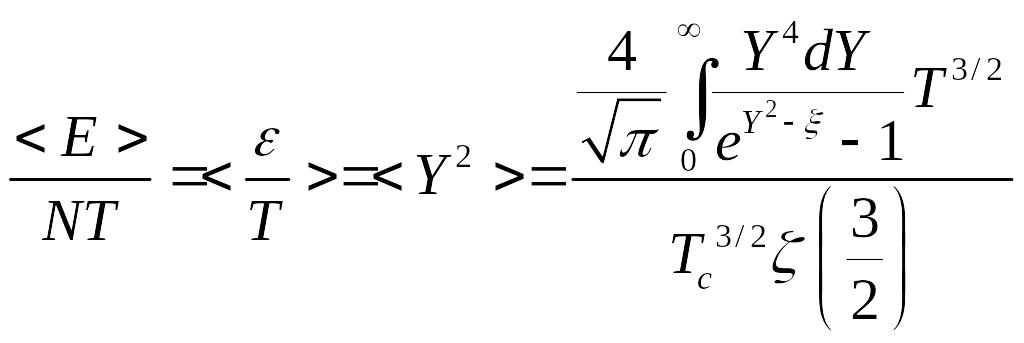
Как мы получили этот результат:
далее ввели обозначение
Мы имели:
Полное число частиц
Итак, имеем:
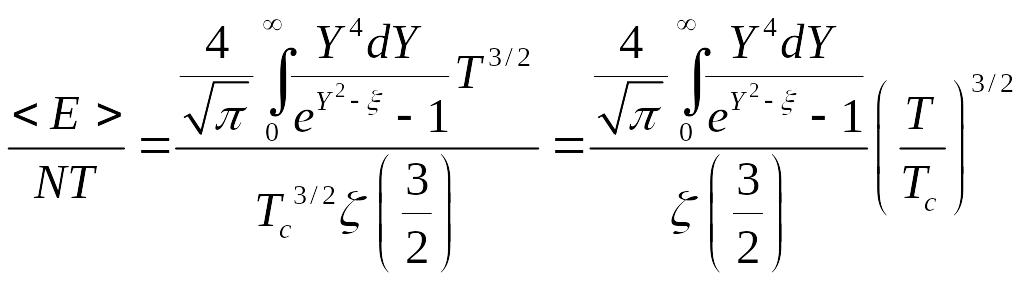
Таким образом, имеем:
Рассмотрим функции
и
.
Тогда:
Сделаем замену переменных:
Аналогично можно получить:
Итак, имеем:
(32)
(33)
Рассмотрим результаты (32) и (33) в области . В этой области , т.е. . Тогда переходим к функции Римана:
и
В термодинамике
и
.
Мы определили
из условия
,
тогда из (33):
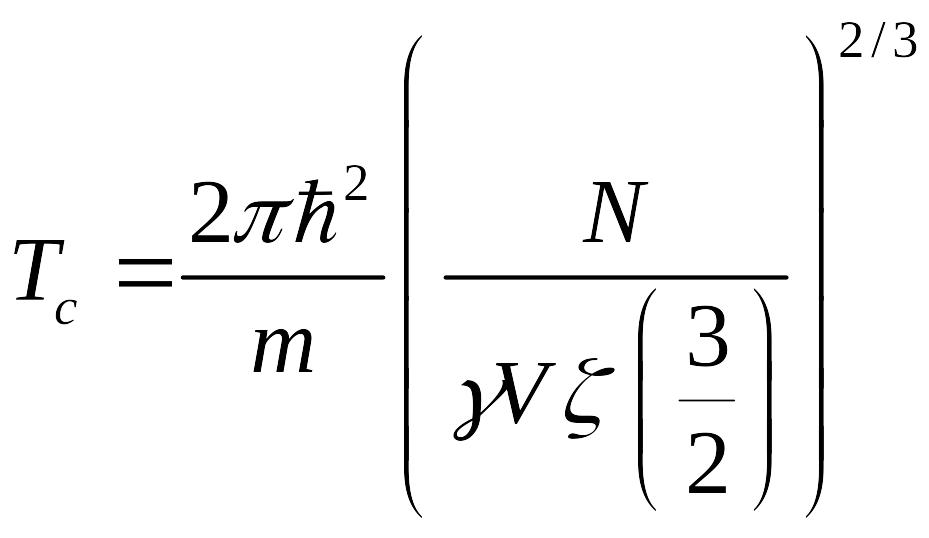
Тогда при получаем:
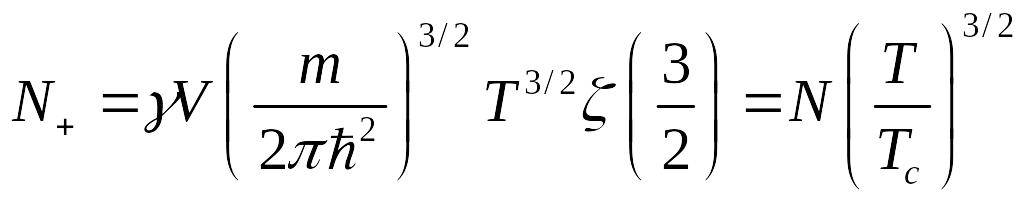
Запишем такое соотношение:
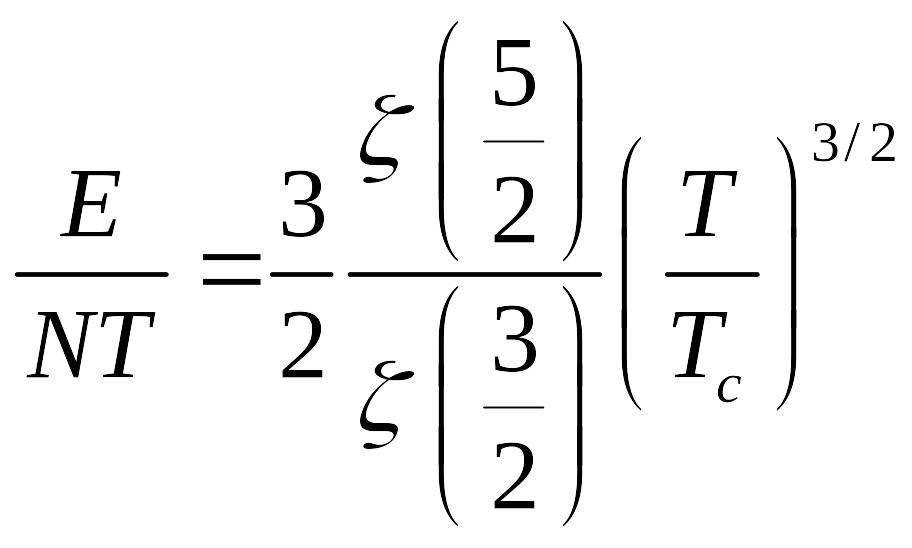
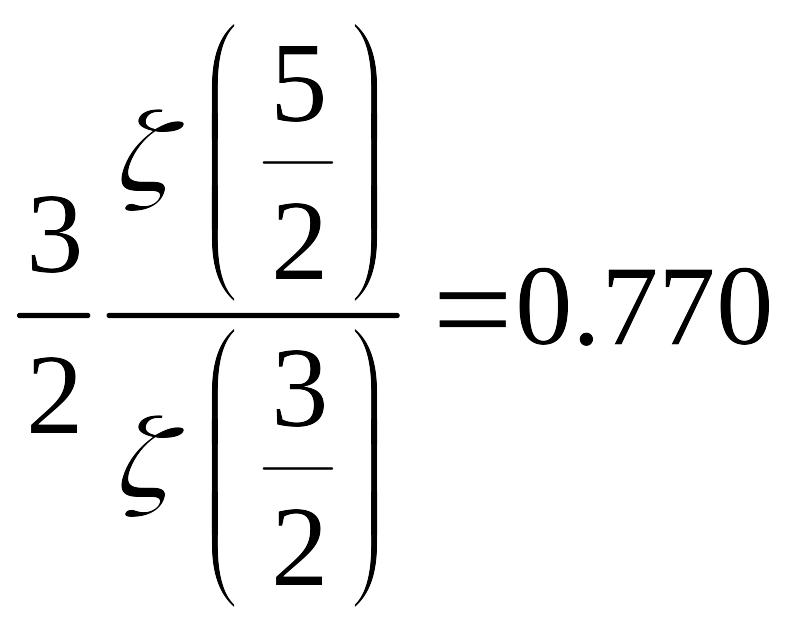
Тогда:
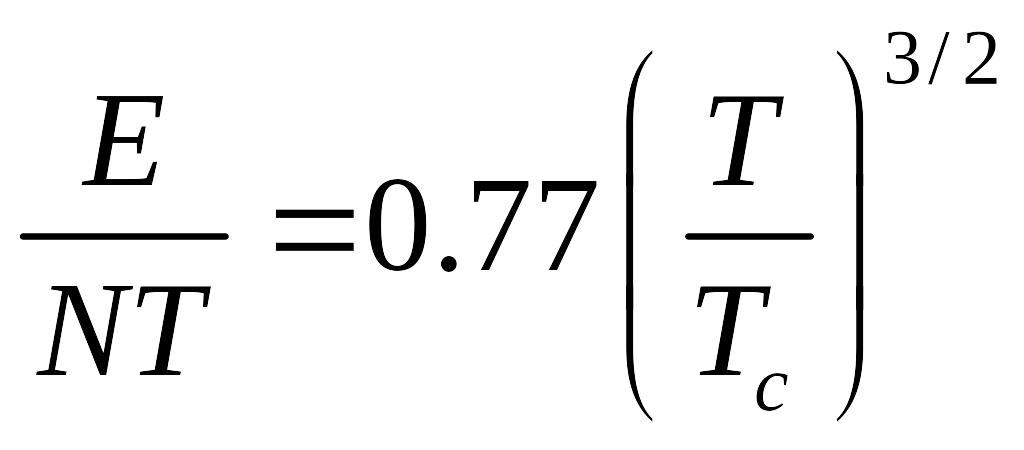
Найдём теплоёмкость при постоянном объёме:
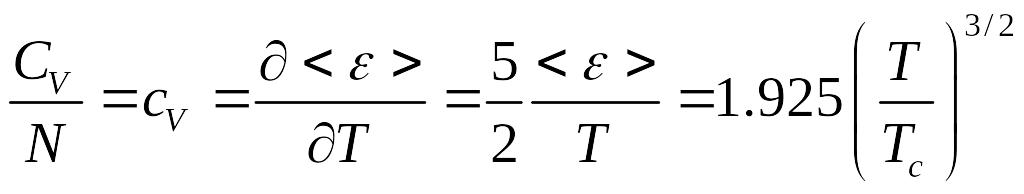
где - средняя энергия одной частицы.
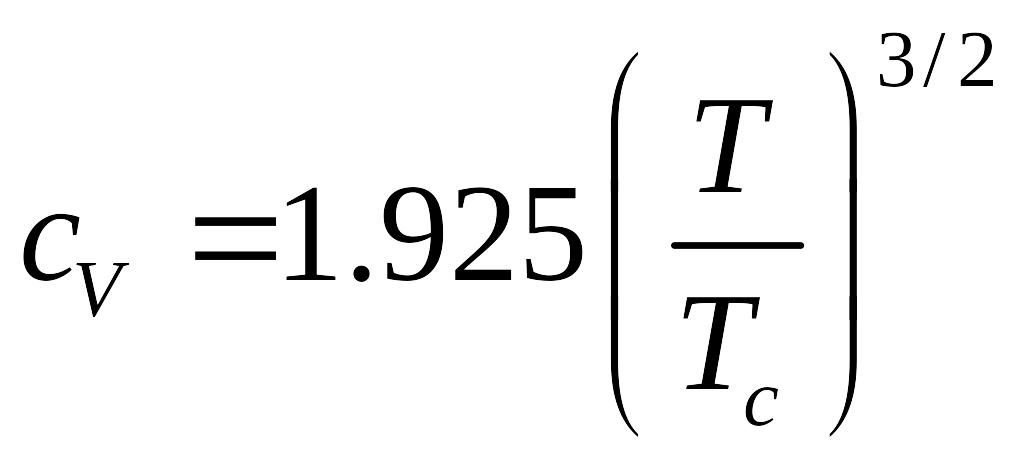
- это точка фазового перехода второго рода, в ней теплоёмкость имеет перелом.
Для парагелия (когда спин равен нулю, а
)
- молярный объём гелия вблизи точки
сверхтекучести,
.
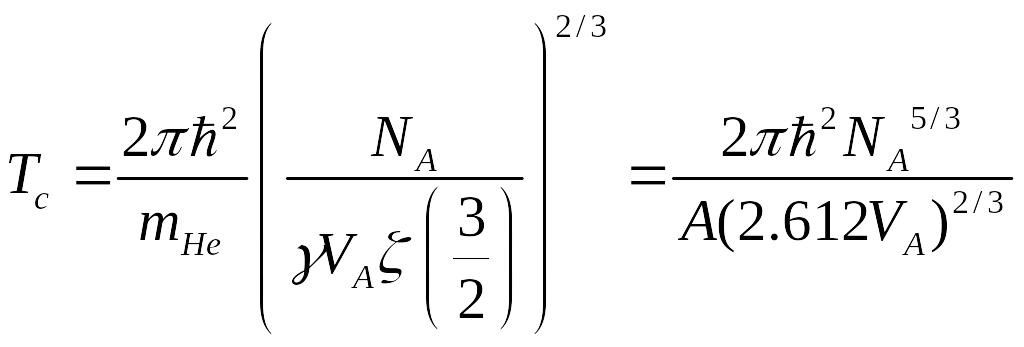
это температура в энергетических единицах, если хотим в градусах, то нужно:
Соответствующие расчёты дают:
С помощью энергии можем посчитать и другие величины. Например, термодинамический потенциал:
Но по определению:
Но так как в области имеем , поэтому:
Тогда можем посчитать свободную энергию Гельмгольца:
Исходя из первого начала термодинамики можем посчитать энтропию:
Для нашей области имеем:
Видим, что при
имеем
,
так как при
получаем
Для давления имеем:
По сути дела это уравнение состояния.
Получили, что давление от объема не зависит. Это возникает когда идёт конденсация.