§6 Плотность вероятности для энергии системы, описываемой каноническим распределением Гиббса.

Запишем каноническое распределение:

Выразим константу через свободную энергию:

, а

Мы писали:

- сумма по всем состояниям.

Проведя суммирование, получим , т.е. энтропия определяется по наиболее вероятному состоянию.

Вообще, исходя из :

Но мы записали только один параметр:

Переходим в квазиклассику:

- это плотность вероятности реализации состояния . Переходим от суммирования к интегрированию:

, где

Для суммы - номер состояния, для интеграла - число степеней свободы( )

Часто представляет интерес получение функции распределения энергии системы.

Точка в квазиклассике не характеризует состояние, а состояние характеризует фазовый объём:

Д ля описания распределения энергии введём функцию . У нас теперь - непрерывная величина. Тогда имеем:

Тогда: , здесь подразумевают интегрирование и сведение к полученному выражению.

- т.е. имеет место интегрирование.

Мы писали, что можем сделать замену интеграла на некое среднее и такие что:

Мы писали, что:

Тогда имеем:

- это как статистический вес

Таким образом мы кривую заменили на прямоугольник:

О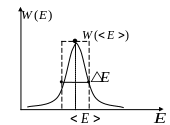 ценка даёт:

- есть некая функция от

Вывод:

, - это функция от среднего значения энергии , т.е.:

Так как энтропия - это функциональная зависимость, то можем перейти от к произвольной , т.е. от переходим к . Мы рассматриваем функциональную зависимость энтропии от переменной энергии:

Можем двигать по оси энергий и смотреть что это даёт.

И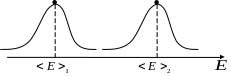 мея соотношение , получаем:

Здесь зависимость от - некая аналитическая связь.

Нам нужно оценить число состояний в интервале энергий .

Тогда:

В этом разложении дальше слагаемые не учитываем – их учёт даёт поправку к Гауссовому закону для . Учёт до третьего слагаемого приводит к Гауссовому закону для .

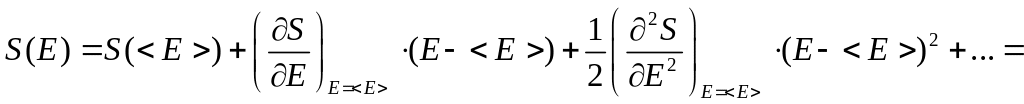
Показатель экспоненты имеем в ви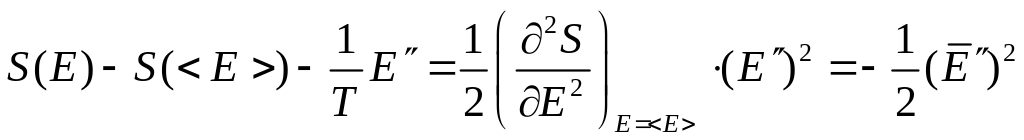де:

, где

Мы получили Гауссов закон распределения. Это есть приближенная аппроксимация, т.к. не учитываем остальных членов в разложении энтропии в ряд.

§7 Аппроксимация Гауссовым законом распределения вероятностей для экстенсивного термодинамического параметра.

Так как энтропия достигает максимума при наиболее вероятном значении соответствующей термодинамической величины, то закон для этой величины может быть получен методом аналогичным как для энергии. Речь идёт об экстенсивных величинах (например об энергии).

Тогда обозначая эту величину через x можем записать вероятность того, что термодинамическая величина x лежит в интервале как:

- это плотность вероятности

в случае энергии мы обозначали как

Константу найдём из условия нормировки:

Тогда:

Итак, имеем:

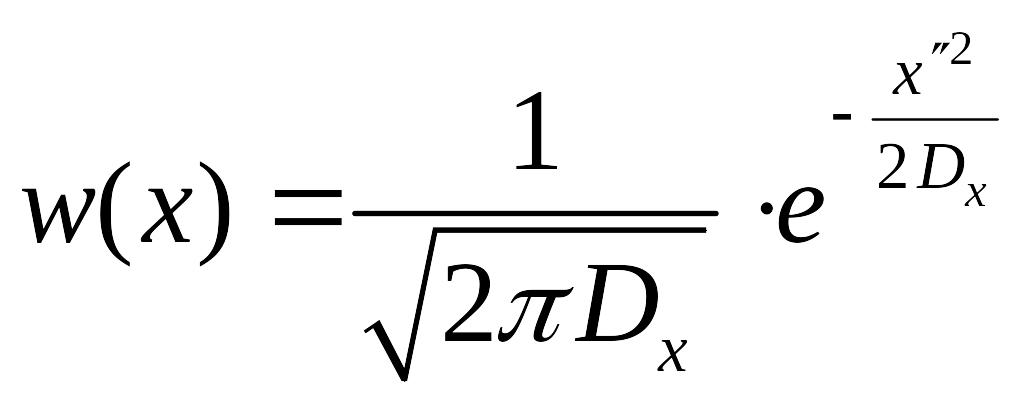
Введём критерий применимости квазиклассического приближения к описанию термодинамических величин. Существует такое соотношение неопределённости:

где - время релаксации, а - неопределённость энергии.

Используем это соотношение для нахождения неопределённости в нахождении энтропии.

Из соотношения получаем неопределённость энтропии :

Тогда имеем:

Поскольку энтропия входит в плотность вероятности:

то неопределённость не должна приводить к влиянию на вероятность термодинамической величины . Поэтому должно выполнятся

Тогда для времени релаксации находим:

т.е. при таком ограничении можем применять квазиклассику в термодинамике.

, ,

Тогда при комнатной температуре.