§4 Расчет параметров вырожденного электронного газа.
Рассматриваем достаточно низкие температуры, которые удовлетворяют ограничению:
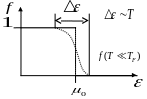
И кривая
незначительно отличается от
при
.
Можно качественно оценить величину теплоёмкости для низких температур.
- число частиц, охваченных возбуждением.
Тогда:
Теплоёмкость
:
- при низких температурах
Это качественная оценка теплоёмкости для низких температур.
Т.к.
мала, то
- это малый параметр, по которому можно
разложить решение.
где
аналогично для химического потенциала:
Зная эти поправки можно точно рассчитать теплоемкость:
Т.е. с учётом
имеем:
где
- теплоемкость на одну частицу.
,
,
Тогда:
- это расчёт с большой точностью
Теперь посчитаем свободную энергию, используя соотношение, связывающее энергию и свободную энергию. В термодинамике имеемся соотношение:
Тогда:
здесь константу вычислять не будем, а будем писать в виде:
- за счёт теплового возбуждения
Тогда:
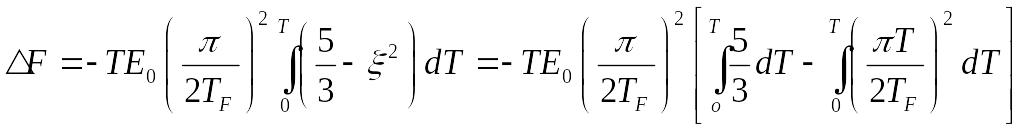
С помощью свободной энергии можем посчитать химический потенциал, энтропию, давление, можно получить уравнение состояния:
Мы знаем связь и :
,
а
,
т.е. надо перейти от одних переменных к
другим – преобразование Лежандра.
Тогда мы можем найти
и
как частные производные от
по соответствующим переменным:
Тогда:
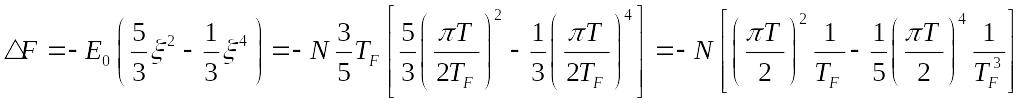
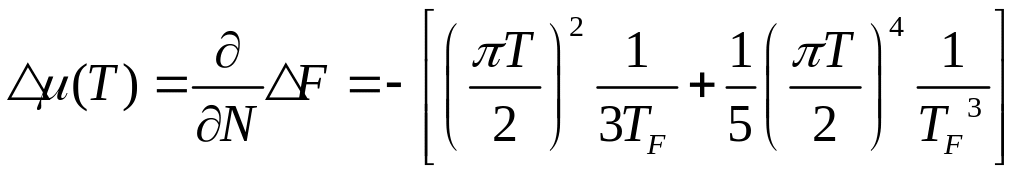
Оказывается, что
,
тогда:
Теперь найдём соотношение для давления:
Тогда:
и мы подтвердили зависимость .
Найдём теперь
,
- известная величина.
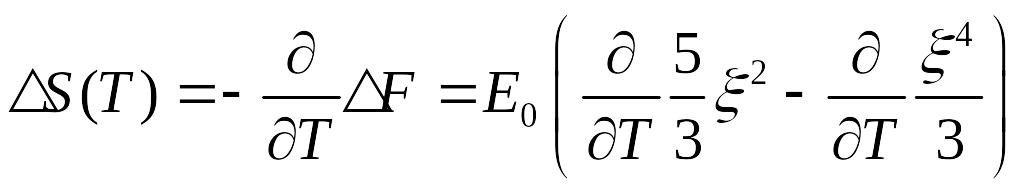
Используем соотношения:
,
,
,
Тогда получим:
Мы получили температурно-зависящий член энтропии. С ростом температуры энтропия возрастает.
§5 Вырожденный Бозе-газ – квазиклассическое приближение.
Запишем функцию распределения Бозе-Эйнштейна:
,
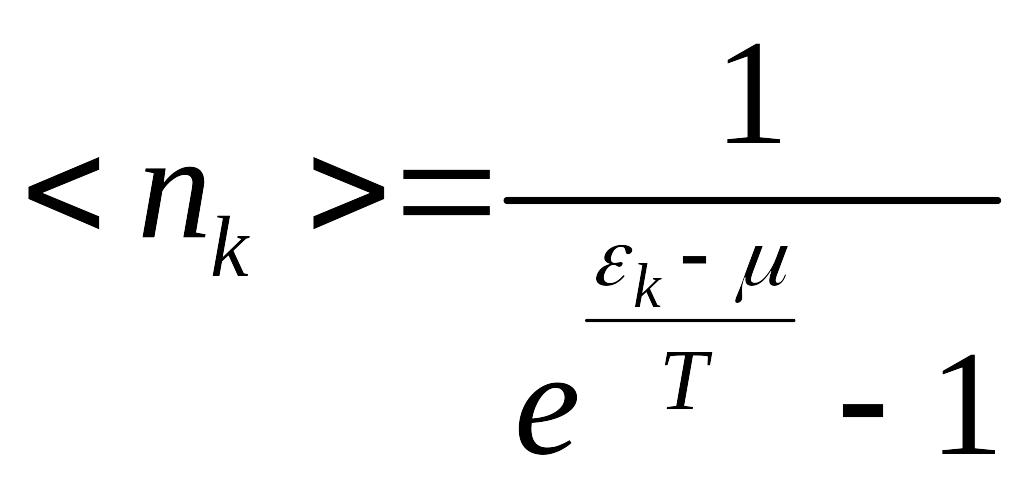где
- номер одночастичного состояния
В квазиклассическом приближении переходим в фазовое пространство:
,
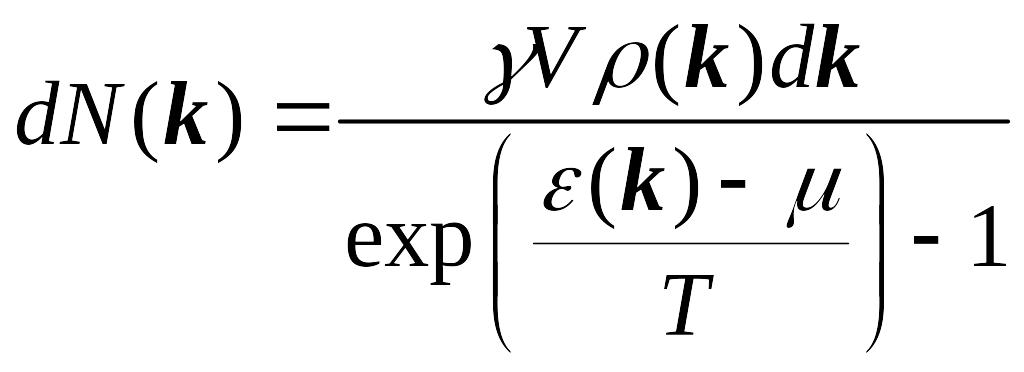
- шести мерное фазовое пространство.
Здесь
.
Полное число частиц в квазиклассическом
приближении:
(30)
Так как энергия не зависит от :
то по можно проинтегрировать.
,
тогда
Выясняется, что переход (30) не является
равенством, поэтому полученный интеграл
обозначим как
:
Дело в том, что интеграл при нулевых
энергиях
обращается в нуль, т.к.
влечет
.
Но на самом деле
,
но
- это и зануляет результат при
.
Таким образом
- это число частиц с положительной
энергией
.
Полное число частиц:
где
- число частиц с нулевой энергией
.
находится из
- надо суммировать по всем состояниям
где
,
а именно:
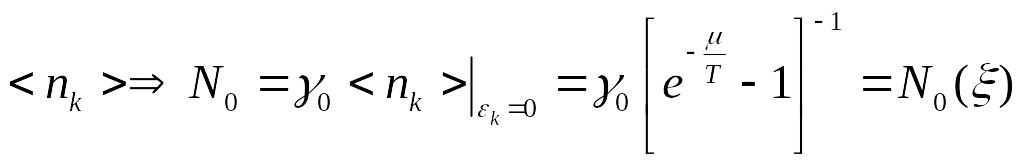
Это есть некоторая функция от
.
Для Бозе частиц
.
Теперь модифицируем функцию , в ней тоже введём переменную :
Введём переменную
,
тогда
.
Тогда:
Можем найти:
Значит
и тогда:
Аргумент экспоненты
,
тогда:
Тогда имеем:
Введём удобную константу:
Константа
уже встречалась при расчёте химического
потенциала.
Интегрирование по телесному углу даст:
Тогда будем иметь:
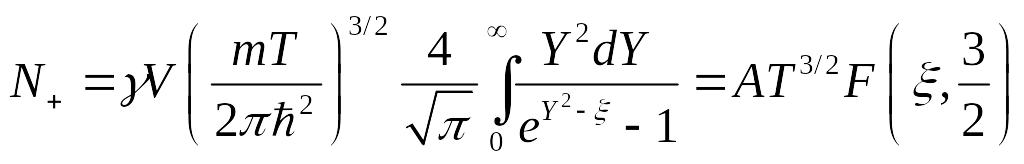
где
,
а
- функция от
Посмотрим теперь на функцию
:
,
где
Посмотрим как функции и зависят от . Легко видеть, что:
и
т.е. с ростом эти функции возрастают.
возрастает – это значит что возрастает
,
т.к.
.
Так как 0 отрицательное, то его рост – это значит убывание по абсолютной величине.
Возрастание
Тогда убывание приводит к убыванию и следовательно к убыванию функций , и .
Функция
имеет некоторый максимум при
,
т.е.
не может превысить нуль. Тогда ограничение
для
:
так же убывает при убывании
.
Существует некоторая температура
при которой
равен полному числу частиц
.
Такая температура называется температурой
конденсации
.
Тогда имеем определение:
,
где
.
- это функция Римана:
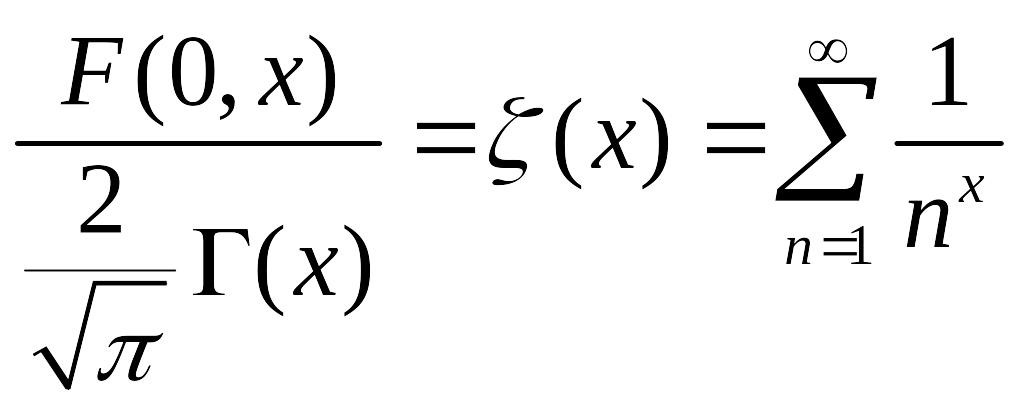
Оказывается, что
.
Тогда зная , можем рассчитать температуру конденсации .
Если понизим
ниже
,
т.е.
,
то в уравнении
(31)
н
ет
решения для химического потенциала.
Это уравнение при заданных
и
является уравнением, определяющим
химический потенциал.
Т.е. при
не можем вычислить
из уравнения (31) классическим образом.
Как решают уравнение (31):
при
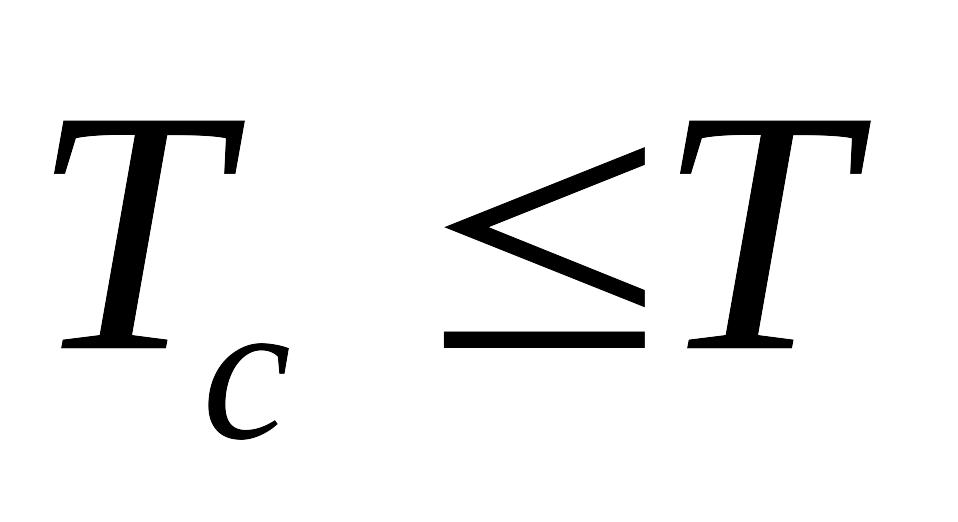пренебрегают
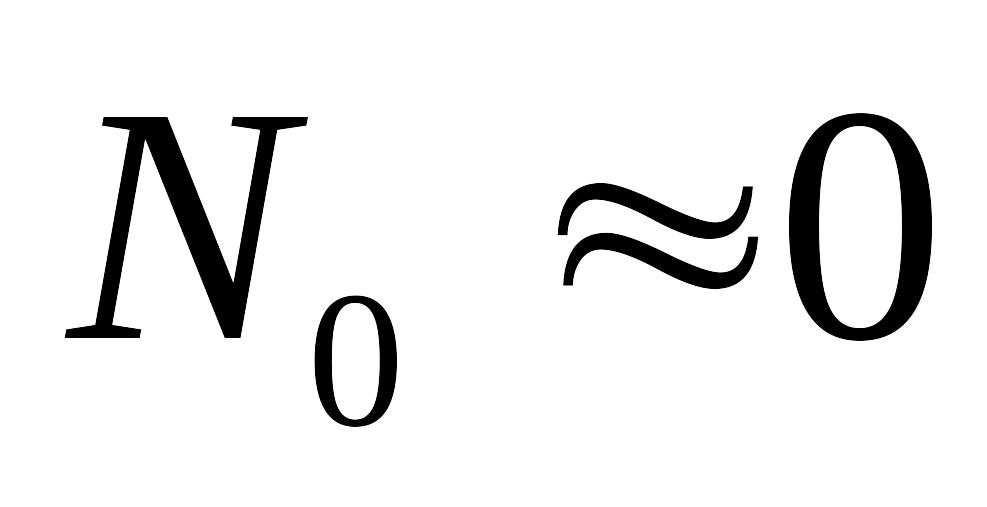и решают получая
при принудительно полагают
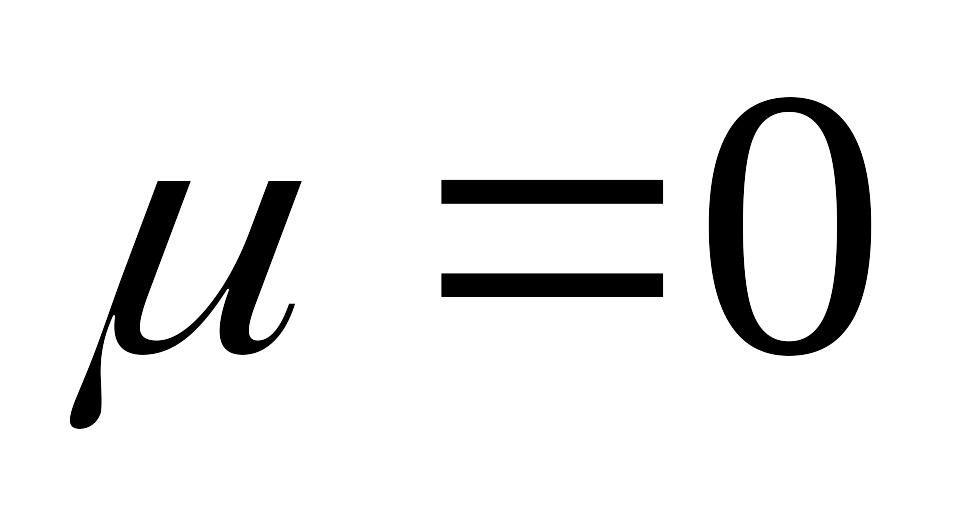для оценки
Тогда при
имеем:
Тогда разность
дает число частиц на нулевом уровне.
Тогда:
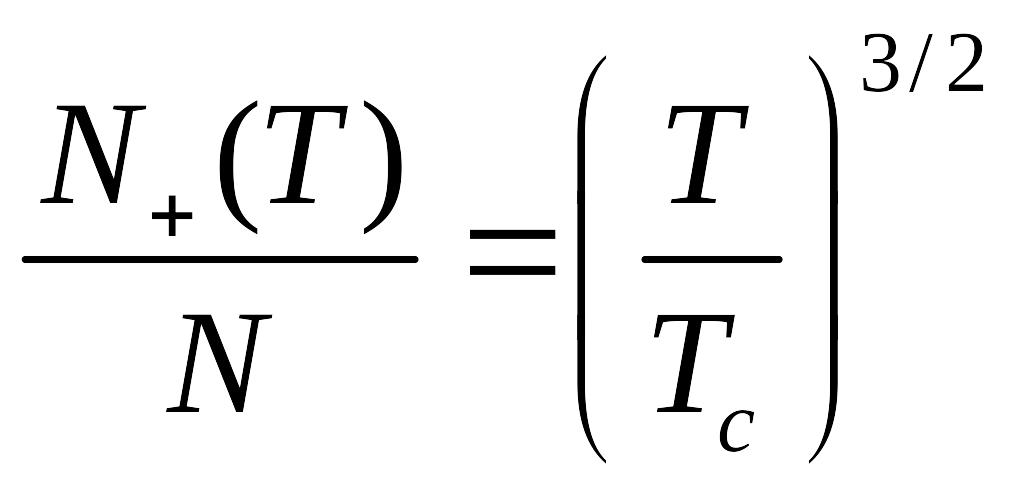
И, следовательно, имеем:
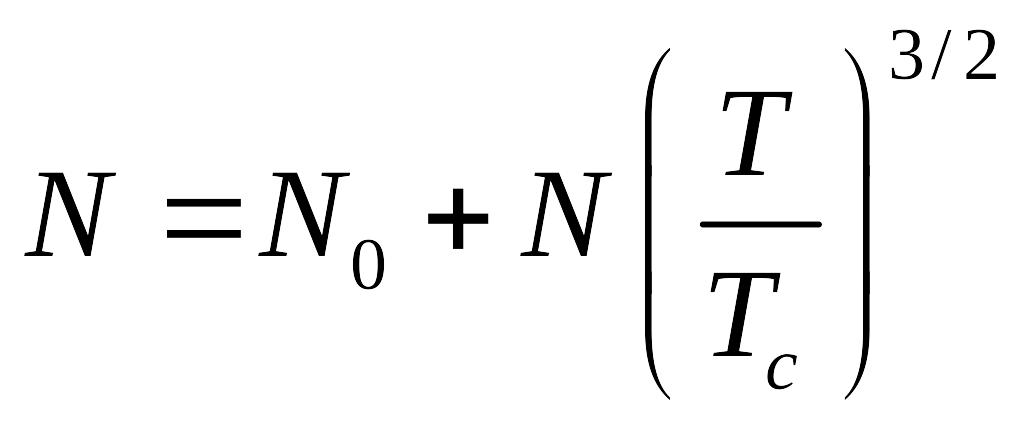
- отсюда находим число частиц на нулевом
уровне
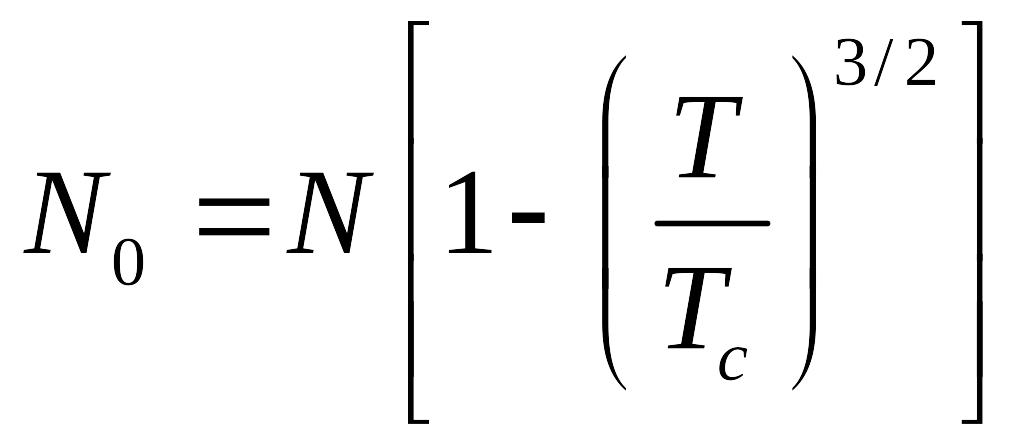
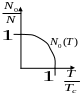
При
все частицы переходят на нулевой уровень
энергии.
Речь шла не о реальной конденсации, а о конденсации в импульсном пространстве.
Проводили оценки для парагелия и получали значение температуры:
Это называется
- точкой гелия.
Если оценить по нашим формулам, то получится:
Переход всех частиц на основной уровень называют Бозе-Эйнштейновской конденсацией.