§2 Тензорная функция Грина волнового уравнения.

Рассмотрим

Оператор

Определим тензор Грина оператора равенствами:

, при (*)

, при

В начале координат в момент времени действует единичная сосредоточенная импульсная сила, плотность которой равна:

(**), - единичный вектор нормали.

Тензор Грина определяет компоненту смещения , возникающую в точке в момент времени под действием единичного импульса, приложенного в направлении координатной оси в момент времени :

Учитывая (**) получаем:

Вычислим динамический тензор Грина для неограниченной изотропной среды. Воспользуемся интегральными преобразованиями Фурье.

Для изотропной среды оператор :

после преобразования Фурье он примет вид:

А уравнение (*) перейдет в алгебраическое:

Тогда имеем:

Умножим это выражение на , тогда:

Тогда находим, что:

(***)

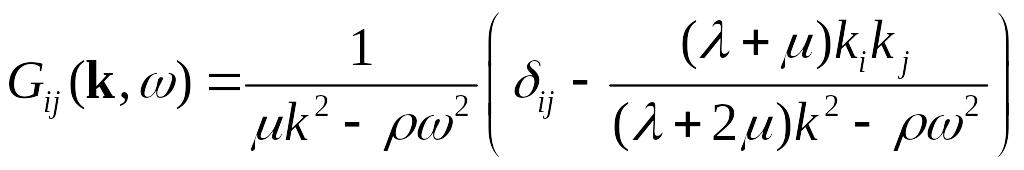Учтем, что и . Тогда перепишем (***) в следующем виде:

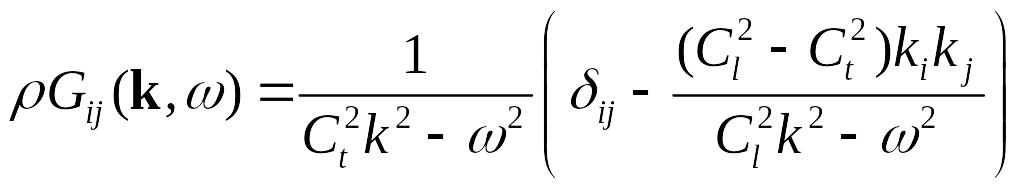
Теперь будем осуществлять переход .

Для вычисления интегралов и воспользуемся теоремой о вычетах.

Пусть - угол между и . Обозначим . Введём сферические переменные .

, тогда .

Следовательно .

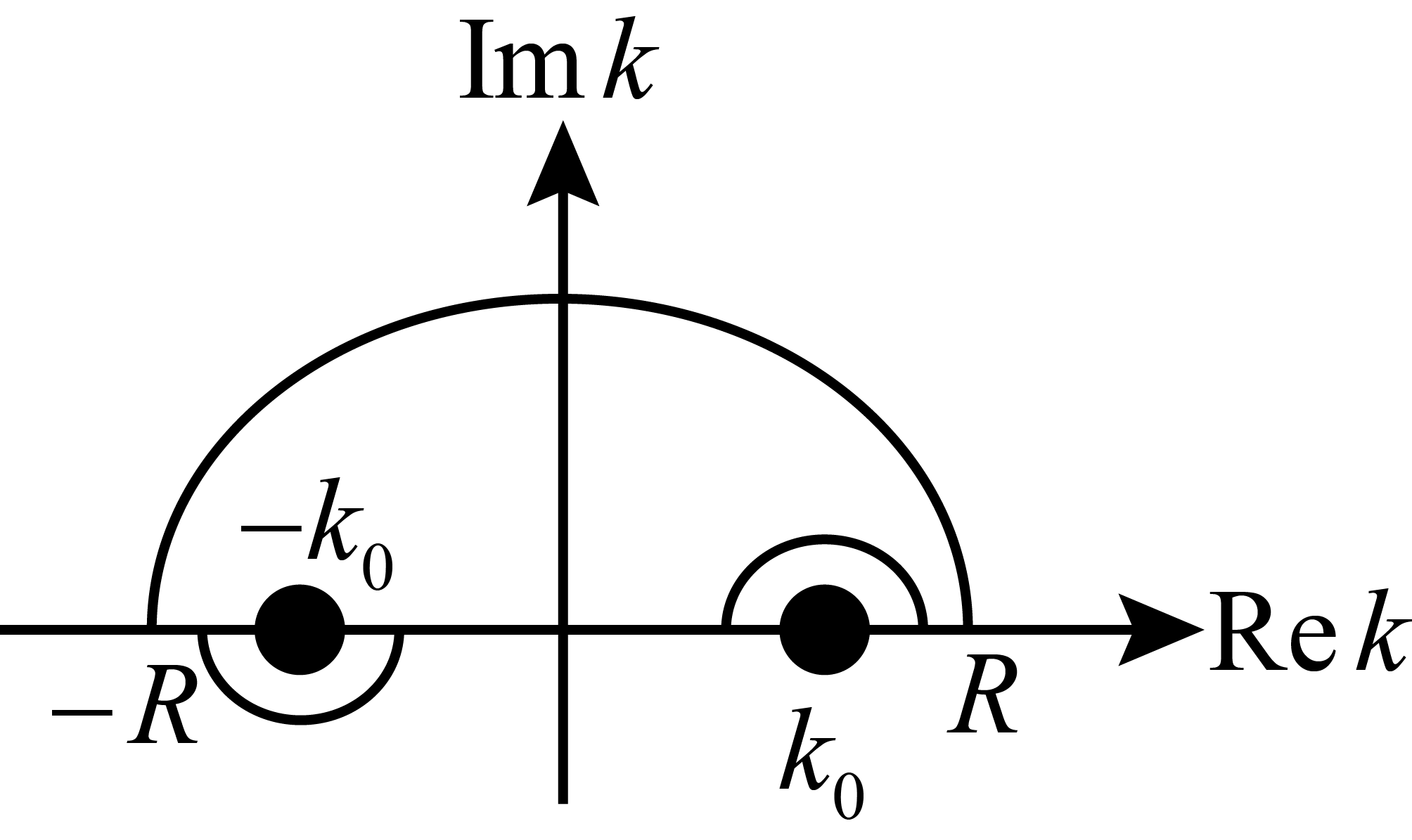
У этих интегралов есть два полюса: и . Надо использовать при расчёте полюс , чтобы получить физически обоснованную асимптотику. Переходим в комплексную плоскость, замыкаем контур обхода сверху. Используем фиктивный переход:

Это позволяет получить нужную асимптотику.

Применяя теорию вычетов, находим значение интеграла .

В силу физических соображений знак в экспоненте меняем на “-”.

По аналогии вычислим интеграл .

В силу физических соображений знак в экспоненте меняем на “-”.

Тогда получаем:

Проводя дифференцирование и используя соотношения:

и , где

Получаем:

,

где

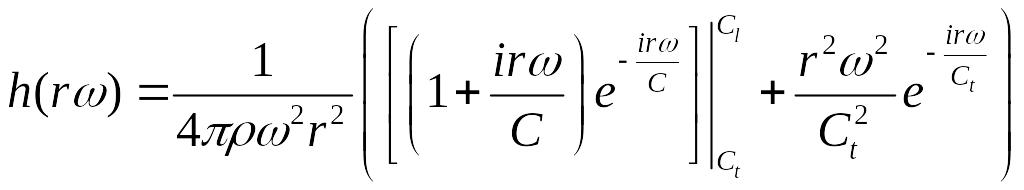
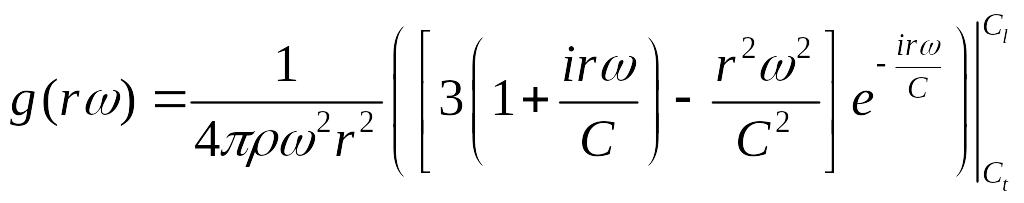
Осуществим переход в пространство оригиналов по времени . Воспользуемся соотношениями:

,

Тогда получаем в итоге:

,

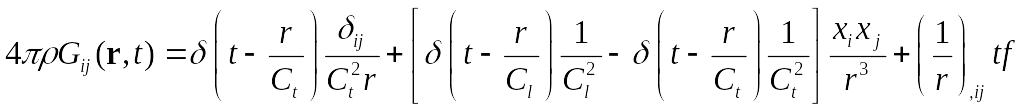где , при и , при остальных .

§3 Уравнение состояния квантового идеального газа. Обменные эффекты.

Уравнение состояния – это уравнение, связывающее переменные .

Мы знаем выражение для свободной энергии Гельмгольца :

Отсюда удобно получать давление:

Выражение для термодинамического потенциала:

Получив мы сможем найти , тогда сможем получить уравнение состояния. Займёмся расчётом . Мы получали для :

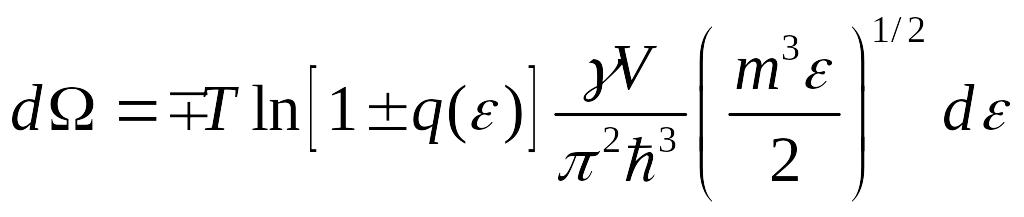
Воспользуемся этим выражением:

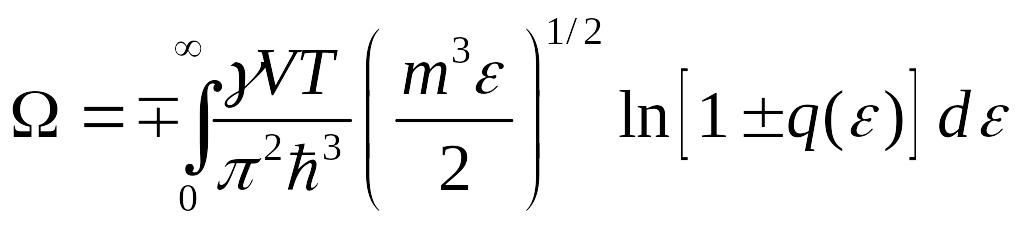
Интегрируем по частям и сводим это выражение к интегрированию по энергии.

, а

Тогда:

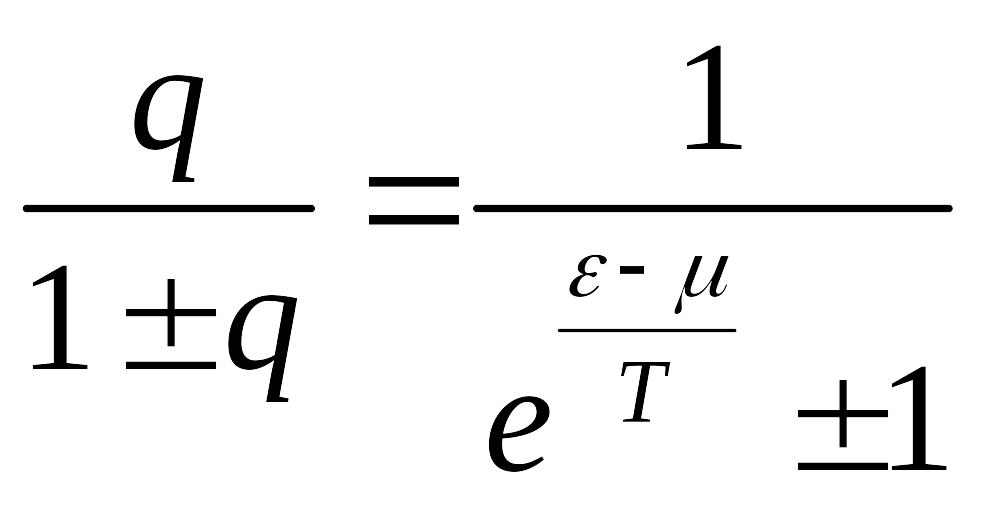
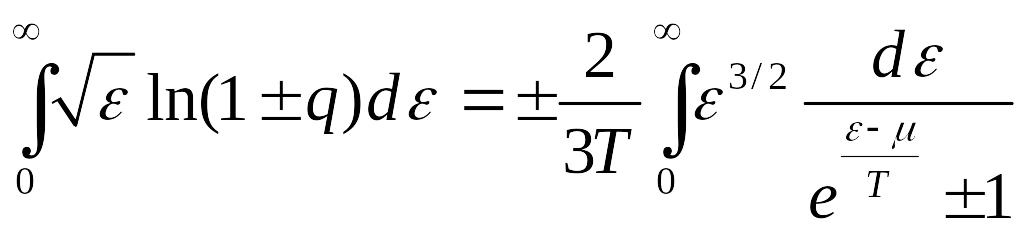
Тогда для получаем:

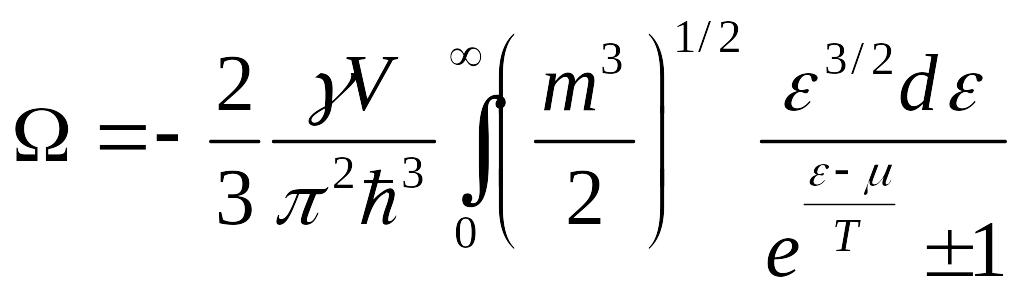
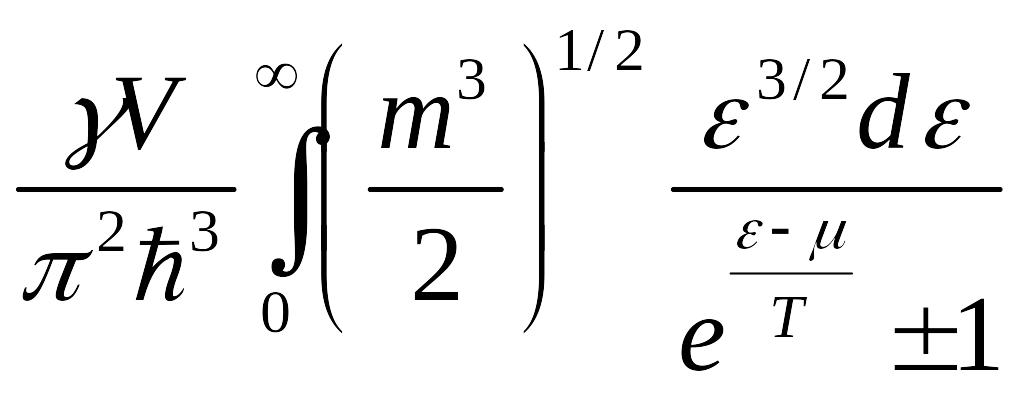- это есть полная энергия системы, тогда:

Теперь имеем соотношения:

Тогда:

В результате получаем:

Это соотношение выполняется ещё и для классического идеального газа. Но для Больцмановского идеального газа было:

, и

У нас газ – квантовый, поэтому соотношение для боле сложно, оно даётся интегралом:

Нам следует рассчитать этот интеграл, он берётся приближенно.

В классическом случае было и . В квантовом случае:

- когда в этом выражении пренебрегаем единицей, то получаем Больцмановское распределение. Мы учтём единицу до первого порядка малости. Для этого разложим в ряд:

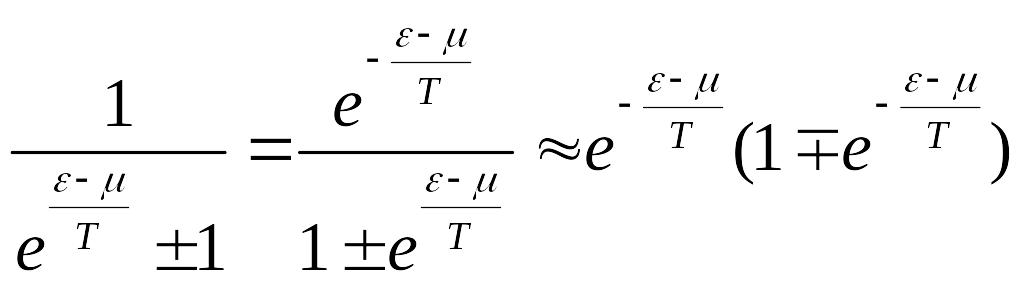
Теперь подставим это в наш интеграл:

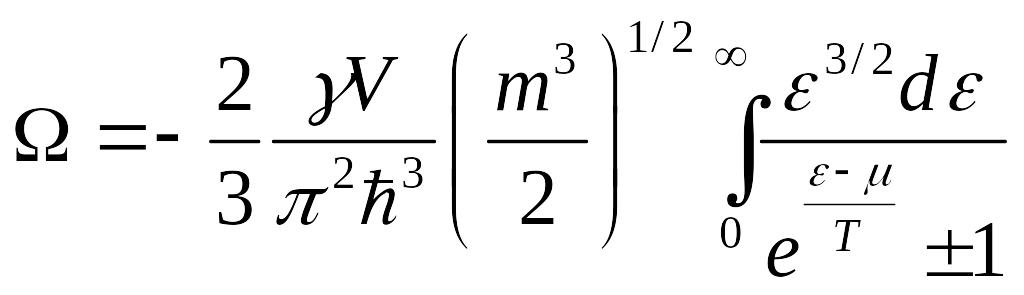
Введём переменные:

и

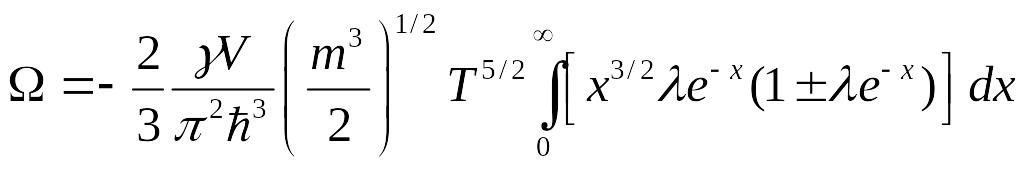
Этот интеграл распадается на два. Первое слагаемое даёт Больцмановскоий результат(классический), а второе дает квантовую поправку, поэтому:

И уравнение состояния:

Запишем :

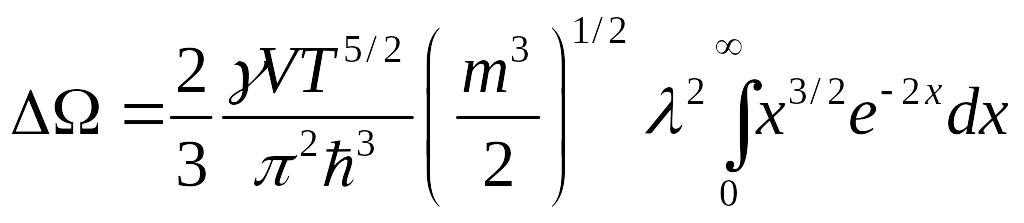
Этот интеграл сводится к гамма-функции. Вводится обозначение:

, отсюда

Тогда:

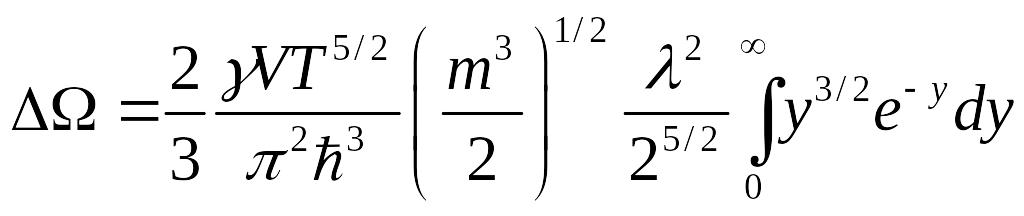
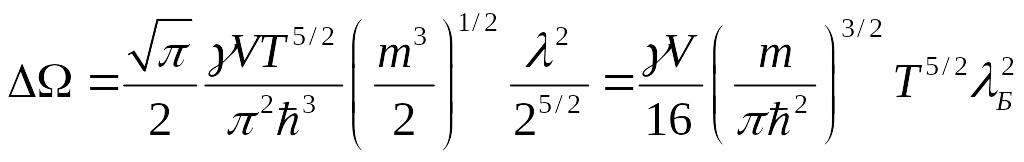
- сюда сделаем подстановку Больцмановского приближения химического потенциала .

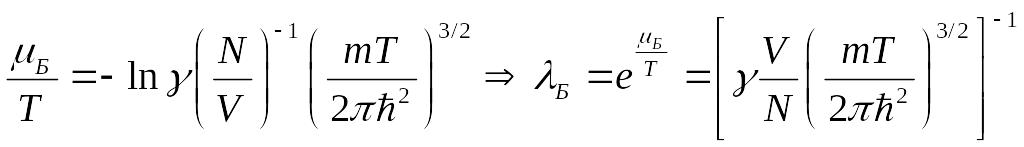
Тогда:

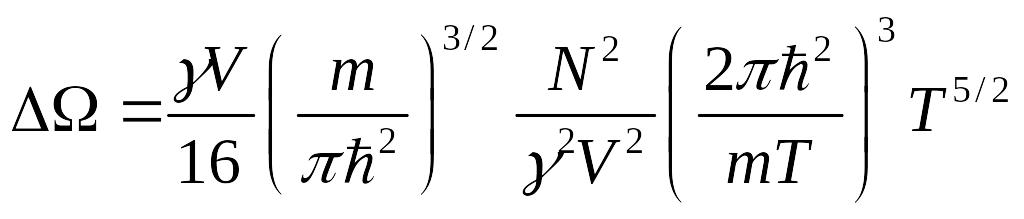
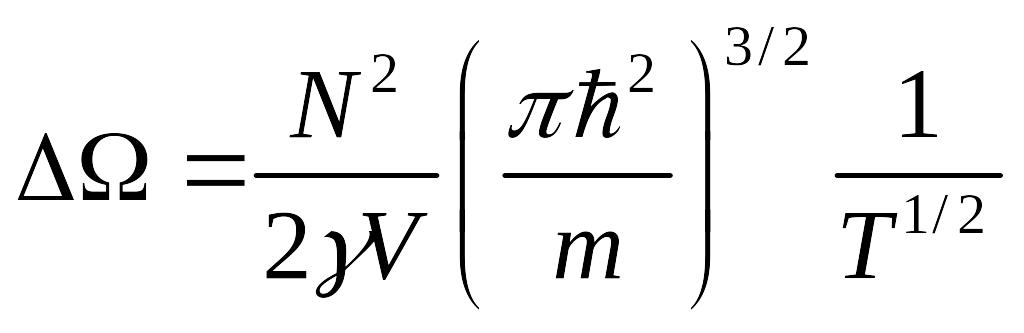
И мы оценили квантовую поправку к термодинамическому потенциалу .

Так как свободная энергия , то её можно представить как , т.к. , причём, как видно .

Найдём поправку к уравнению состояния. Уравнение состояния получается дифференцированием свободной энергии оп объёму :

,

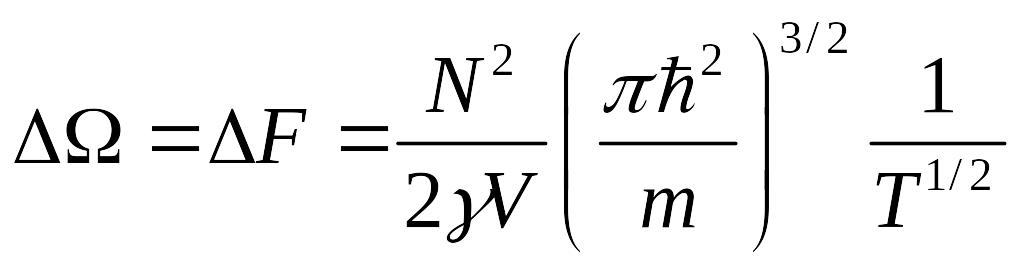
Тогда:

Напомним, что - это из уравнения состояния.

Обозначим:

Тогда:

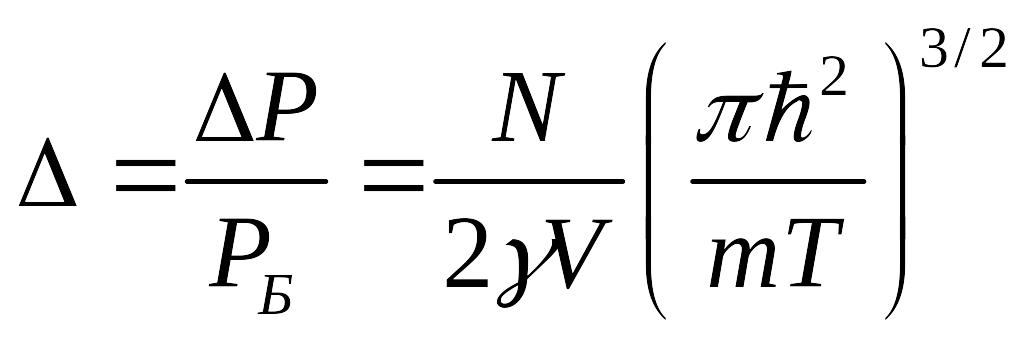
Таким образом, получили уравнение состояния в виде:

Добавки за счёт квантовых свойств системы оказываются в зависимости от систем частиц различными:

«+» - для Ферми-Дирака

«-» - для Бозе-Эйнштейна.

Это называют обменными эффектами, которые обусловлены симметрией волновых функций(симметрией или антисимметрией – т.е. зависит от спина).