§3.8 Основное состояние атома гелия.
Рассмотрим основное одночастичное состояние:
.
Здесь удобно перейти к атомным
(кулононовским) единицам, чтобы исключить
константы
,
,
,
тогда
.
В кулоновских единицах одночастичная функция для основного состояния выглядит:
.
Каким квантовым числам соответствует
одночастичное состояние? Вводят три
квантовых числа (без спина):
,
,
.
Для основного одночастичного состояния
1, 0, 0 соответственно.
Тогда, ставим индексы
.
Эта функция нормирована на единицу, т. е.
.
Если взять симметричные и антисимметричные функции для двух частиц в основном состоянии, то имеем:
,
.
И получаем, что основное состояние описывает симметричная функция. Вычисление энергии одночастичного состояния для центрального поля мы проводили и получали в размерных единицах
.
Или в кулоновских единицах
.
,
.
Задача
Определить приближенно энергию основного уровня атома гелия (ядро с зарядом Z и два электрона), рассматривая взаимодействие между электронами как возмущение.
Решение
В основном состоянии иона оба электрона находятся в S-состояниях. Невозмущенное значение энергии равно удвоенному основному уровню водородоподобного иона:
.
Поправка первого приближения дается средним значением энергии взаимодействия электронов, взятом по состоянию с волновой функцией
.
(произведение двух водородоподобных
функций с
)
Интеграл
проще всего вычислить так
,
,
.
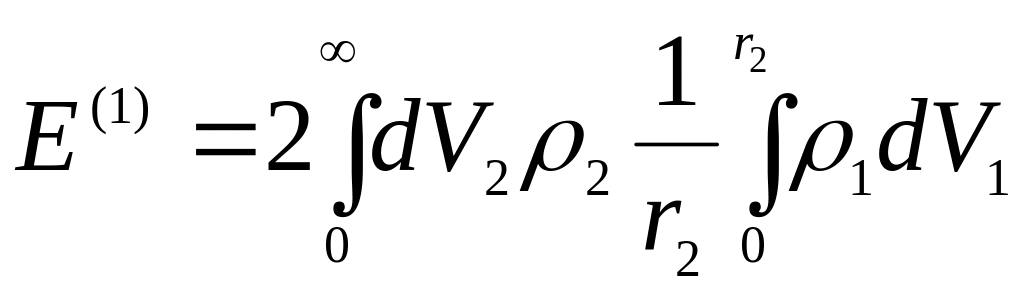Энергия распределение зарядов
в поле сферически – симметричного
распределения
.
Подынтегральное выражение интеграла
по
есть энергия заряда
в поле сферы
.
Множитель 2 перед интегралом учитывает
вклад от конфигураций, в которых
.
Вычислим интеграл
.
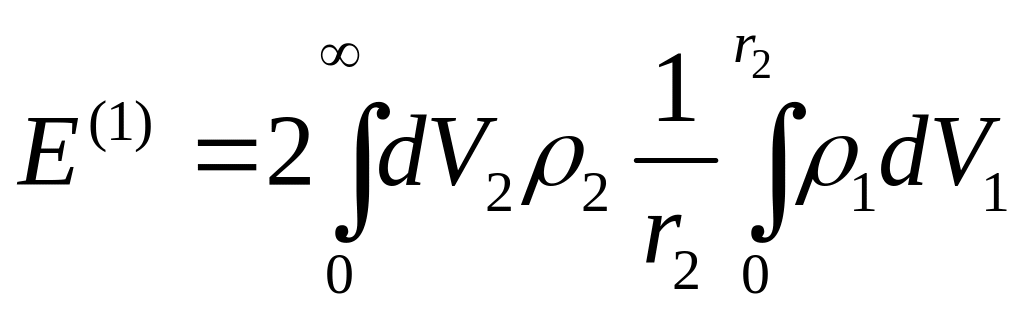Для начала определимся с тем, что нам
считать за
и
.
Из выражения
следует,
что
,
.
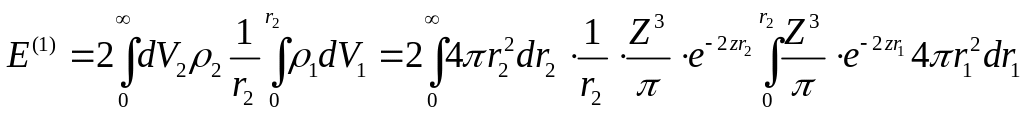
Вынося все константы за знак интеграла в итоге получаем:
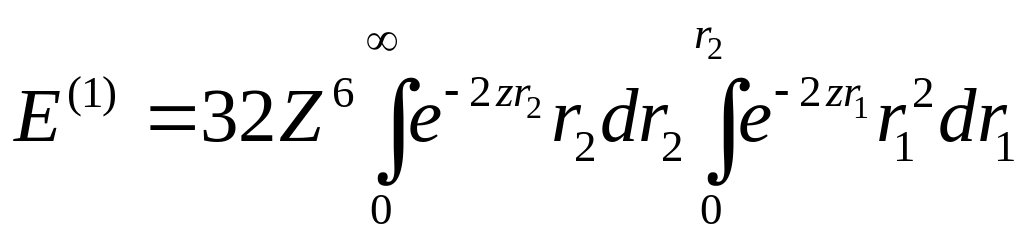
Обозначим за
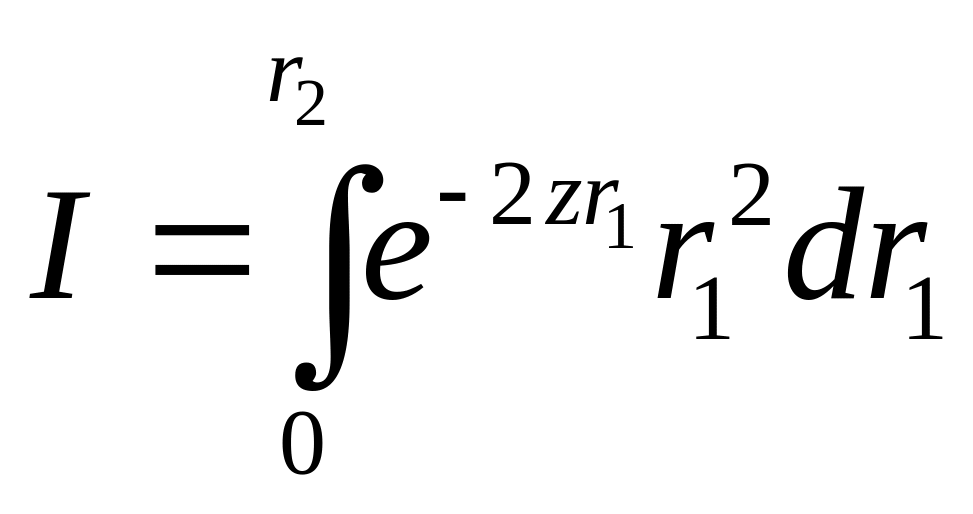правую часть интеграла и посчитаем его
первым.
Таким образом, получим
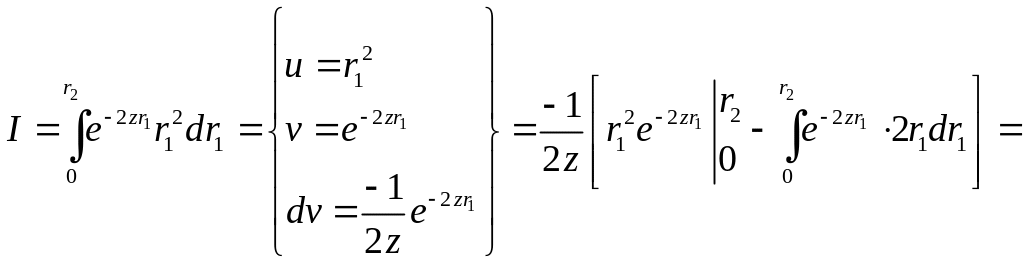
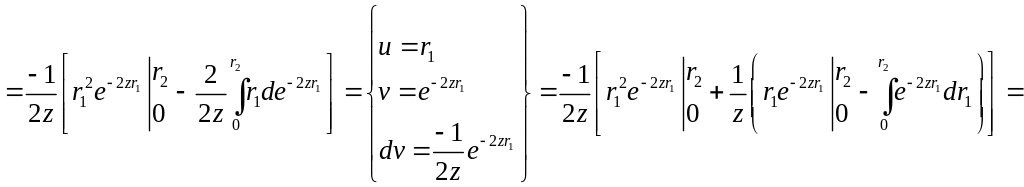
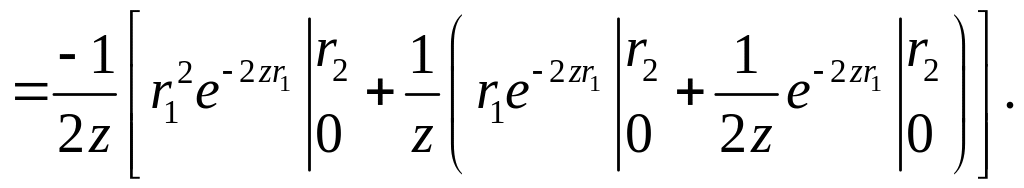
В итоге интеграл I равен:
Подставляя в пределы 0 и
получаем:
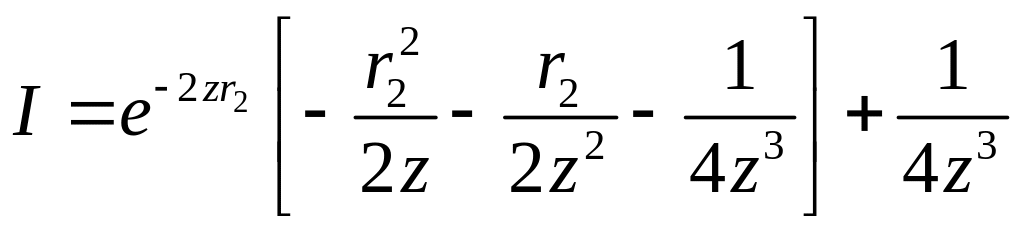
Подставляя интеграл I в наш большой интеграл, получаем:
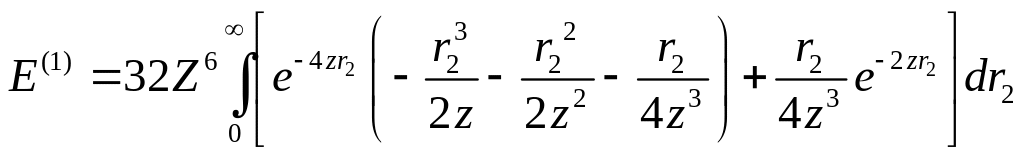
Вычисляем этот интеграл, разбив его на сумму четырех интегралов:
Для решения данных интегралов нам потребуется определение и свойства гамма-функции:
- определение гамма-функции
Свойства гамма-функции:
Складывая
+
+
+
,
получаем:
.
Когда рассчитываем основное состояние,
то функция основного состояния должна
быть
,
однако, ранее мы получили формулу
.
Мы все это рассчитываем через
(53.1)
Однако, правильный результат получается из
.
Тогда в формуле (53.1) стоит при
лишня двойка, которая потом дала
.
Так как у нас два электрона, то есть две частицы, то
.
В первом приближении, энергия основного
состояния для атома Гелия в атомных
единицах
.
В самосогласованном методе решение
оказывается:
.
Факультатив
§1 Упругие волны в изотропной среде.
Сила внутренних напряжений
,
тогда
,
где
- плотность, а
- ускорение. Тогда уравнение движения
имеет вид:
Воспользуемся законом Гука
,
тогда:
,
(*)
здесь учтена симметрия компонент тензора модулей упругости.
Для изотропной среды
.
В компонентах:
,
(**)
где
- коэффициент Ламэ.
Подставляя (**) в (*) находим уравнение движения изотропной среды:
Рассмотрим простейший случай, когда
смещение
неограниченной изотропной среды является
функцией только от одной координаты
.
Тогда получаем волновые уравнения для
отдельных компонент вектора
:
,
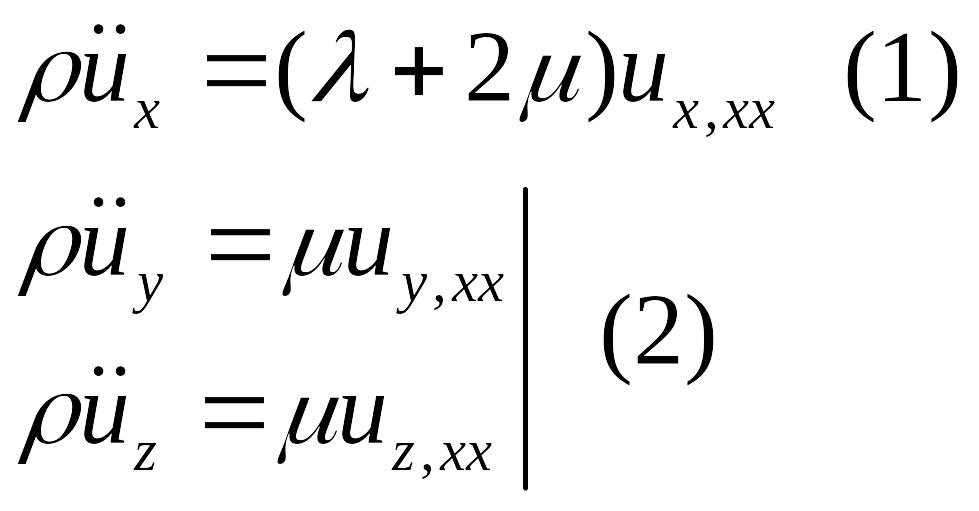где
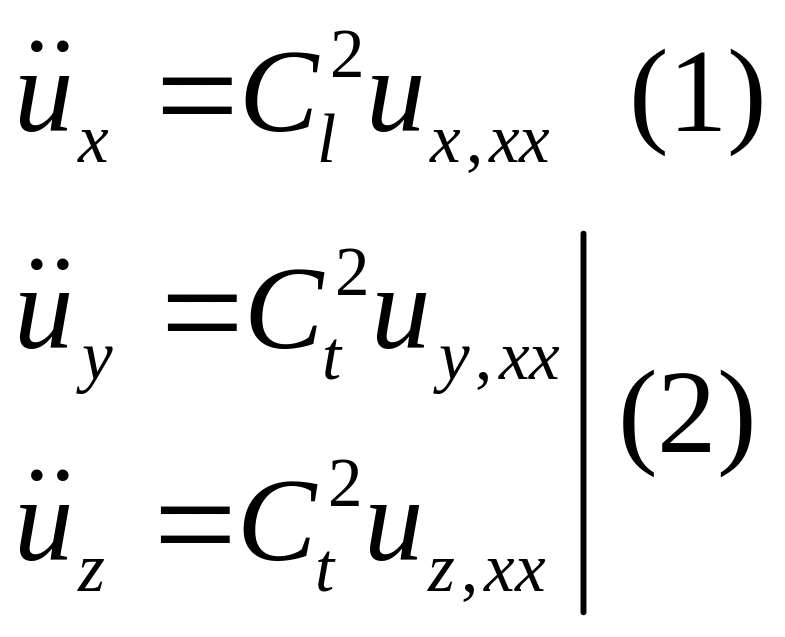
Тогда
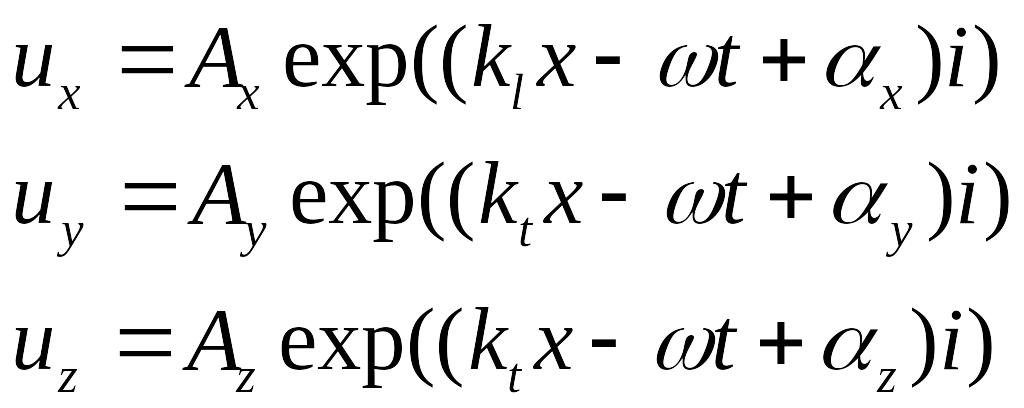
Выражение (1) определяет волну с продольной поляризацией.
Выражение (2) определяет волну с поперечной поляризацией.
Их скорости распространения будут различные:
(***)
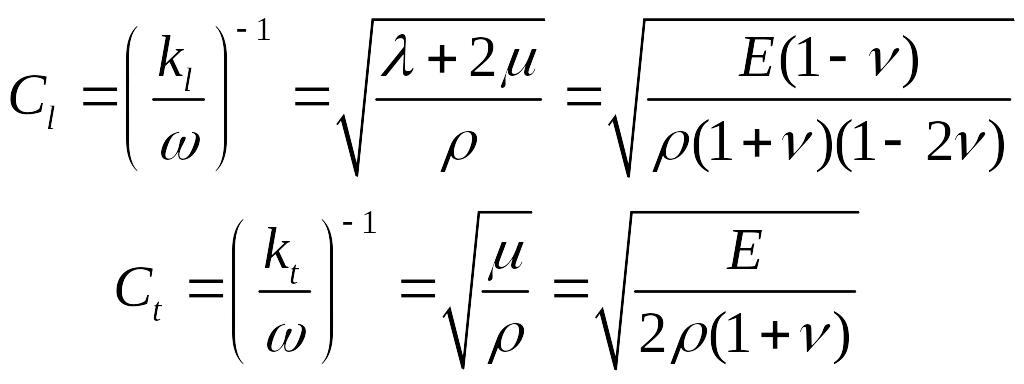Тогда в рассматриваемом случае упругая волна представляет собой три независимо распространяющиеся волны – две поперечные и одна продольная.
Из (***) видно, что
,
т.е. скорость распространения продольных
волн всегда больше, чем для поперечных.
Скорости
и
часто называют продольной и поперечной
скоростями звука.
Для поперечных волн
и
,
т.е. поперечные волны не связаны с
изменением объема.
Для продольных волн
и
,
т.е. эти волны сопровождаются сжатиями
и расширениями. Здесь подразумевалось:
- относительное изменение объема при
деформации.
Уравнение (*) можно записать в операторной форме:
Для изотропной среды:
