§3.6 Уравнение Паули Мы писали волновое уравнение в виде
,
здесь
Для одной
материальной точки
:
Без магнитного поля
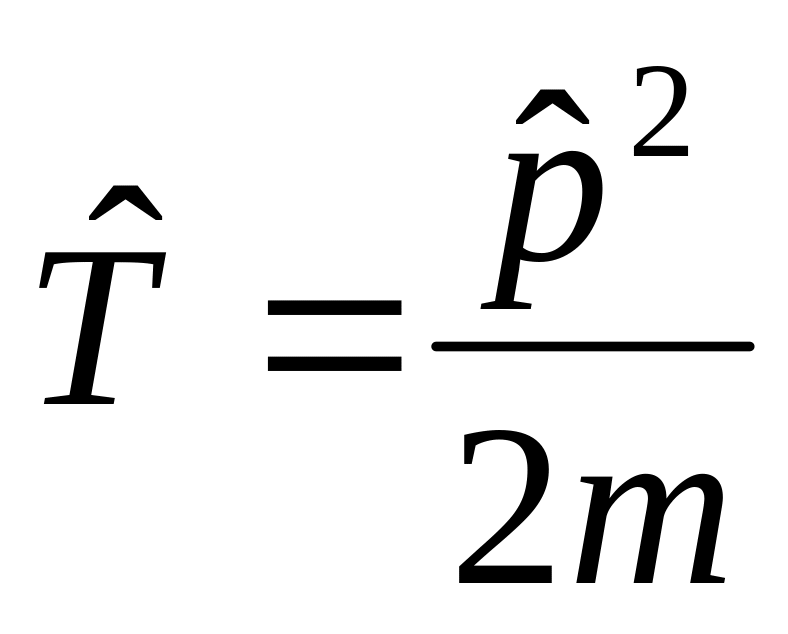.Если есть магнитное поле, то
,
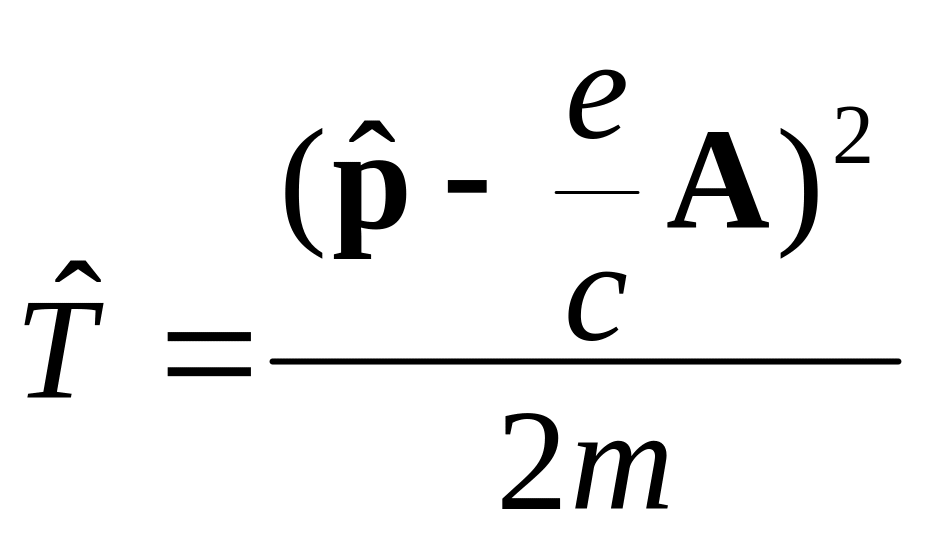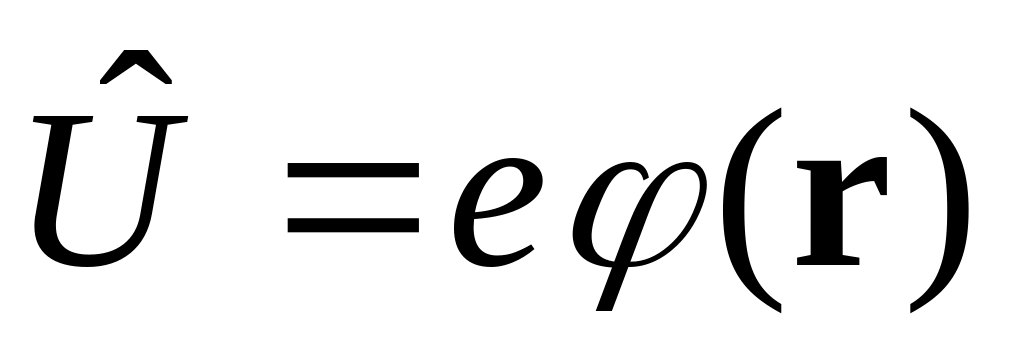
В этих случаях спин не учтен.
С учетом спина модификацию уравнений сделал Паули.
Примечание: уравнения Шредингера и Паули нерелятивистские.
Запишем уравнение Паули:
.
Здесь изменился оператор кинетической энергии.
Без учета магнитного поля
,
где
Здесь
- матрицы Паули
Тогда
.
Покажем, что при отсутствии поля, имеем
,
т. е.
Рассмотрим
={так
как
действует на спиновую переменную, а
на
пространственную, то
и
коммутативны.} =
=
={рассмотрим
сумму, когда
и когда
}=
={рассмотрим
.
,
т. к.
}=[
При
:
Рассмотрим случай, когда есть магнитное поле:
.
Тогда для
оператора
имеем
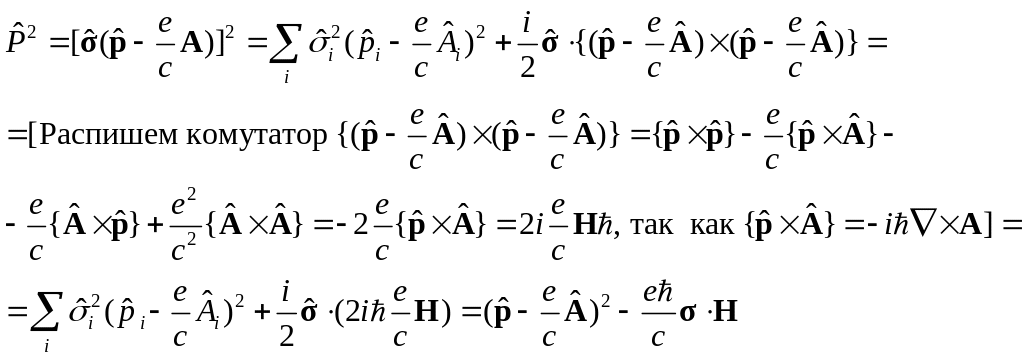
Тогда оператор кинетической энергии из оператора Паули:
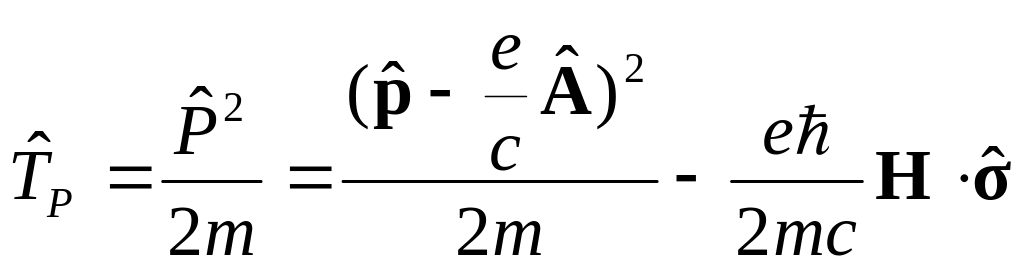
Рассмотрим случай электрона e<0.
(магнетон Бора)
Тогда в итоге получаем:
,
где оператор
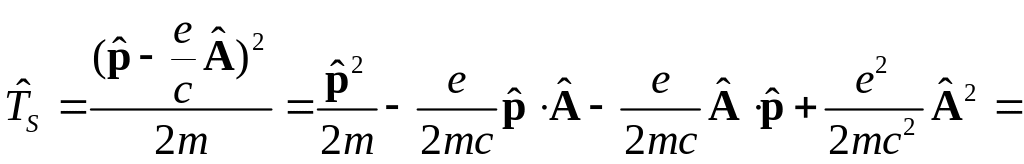
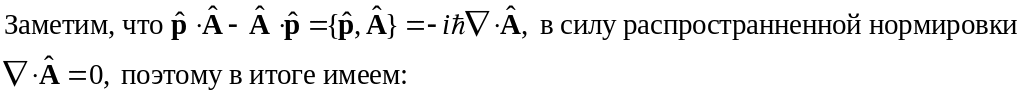
В данном уравнении последний член был опущен ввиду своей малости.
Для оператора Паули тогда получим
,
Отсюда видно равенство для гиромагнитных соотношений
Видно, что магнитные моменты
,
,
механические моменты
Гиромагнитные соотношения
.
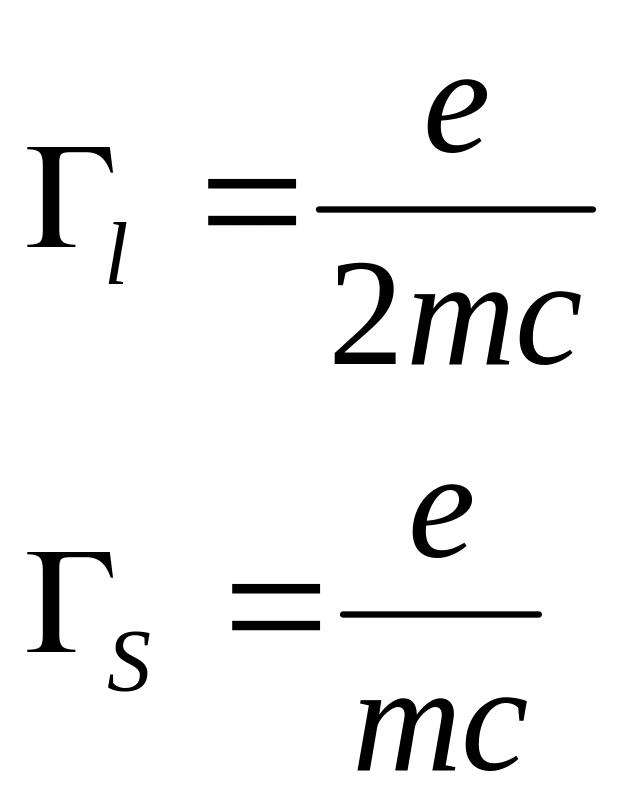Полный магнитный момент
§3.7 Обменное взаимодействие
Рассмотрим пару частиц взаимодействующих друг с другом по кулоновскому закону и находящихся во внешнем поле.
Пусть рассматриваются электроны:
Внешним полем электрона может служить поле ядра.
Одночастичный оператор
, i=1,
2.
Используем принцип Паули несколько в
иной форме, чем мы рассматривали раньше.
Для этого пусть добавка
мала. Здесь спиновое число
.
Суммарный собственный механический
момент:
имеет квантовые числа
.
Учтем влияние спинового момента на волновые функции. Это достигается принципом тождественности. Т. к. электроны – фермионы, то суммарная волновая функция должна быть антисимметричной по перестановке и т. к. в гамильтониане нет спиновой зависимости, то можно разделить переменные, итак:
Эта функция антисимметричная, так как описывает фермионы. Здесь два варианта:
- антисимметричная
- симметричная.
или
- симметричная
- антисимметричная.
Антисимметричная спиновая функция приводит к суммарному спину 0.
Симметричная
спиновая функция приводит к суммарному
спину 1.
Итак имеем 2 типа решения:
Спин
,
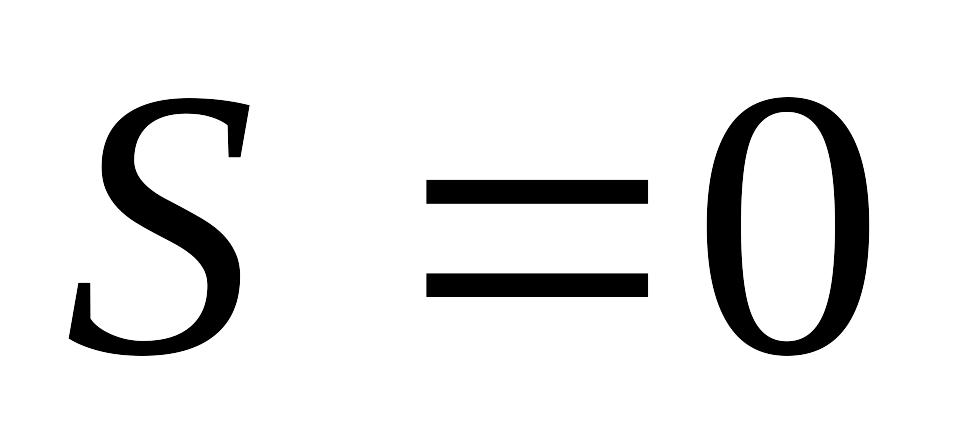симметричная координатная функция по
координатам:
Спин S=1 , имеем антисимметричную функцию по координатам:
Но полная функция
-
антисимметричная.
Случай 1: S=0 – парагелий.
Случай 2: S=1 – ортогелий.
Функции
и
- явно от спина не зависят, но с учетом
принципа тождественности мы получили
два типа решения.
,
- это различные одночастичные состояния,
они удовлетворяют одночастичному
оператору:
, i=1, 2.
Центральное поле.
У нас одночастичные
,
- это все одночастичные состояния.
Имеем задачу на собственные функции и собственные значения.
Функции
и
- описывают невзаимодействующие частицы,
т. е. они являются решением задачи с
оператором:
,
где
,
- одночастичные операторы.
Рассмотрим обменное взаимодействие. Т. к. и является решением задачи для невзаимодействующих частиц, т. е.
Здесь решение не зависит от симметричности
функций, т. е. здесь
.
Для полного оператора
- решение зависит от симметрии функции,
т. е. от спина системы: (0 или 1), здесь
.
В первом приближении теории возмущений найдем энергетические уровни:
,
где матричный элемент оператора возмущения
здесь
=>
.
В нашем случае индекс i складывается из индексов одночастичных состояний 1 и 2.
У нас
,
где K и A – это определенные выражения. Можно рассмотреть матричный элемент для симметричного состояния:
и можно рассмотреть матричный элемент для антисимметричного состояния
.
Это диагональные элементы, т. е. они берутся по одинаковым функциям, т. е. по и .
Подставим функции
и
в матричные элементы
и
и замечаем, что получим одинаковые
слагаемые и различные слагаемые, которые
соответственно обозначим:
,
где
(52.1)
, (52.2)
если учесть перестановку состояний (а не координат), то имеем
(52.3)
В выражении (52.1), (52.2), (52.3) стоят координаты
,
,
а индексы при
обозначают состояния.
Тогда
.
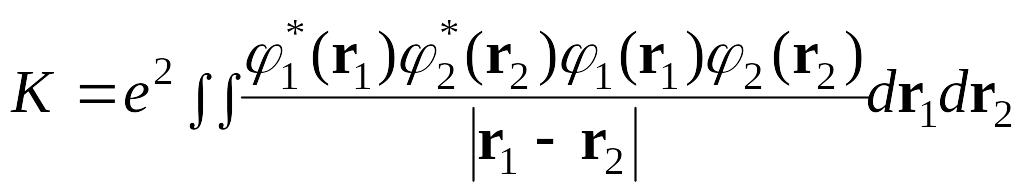
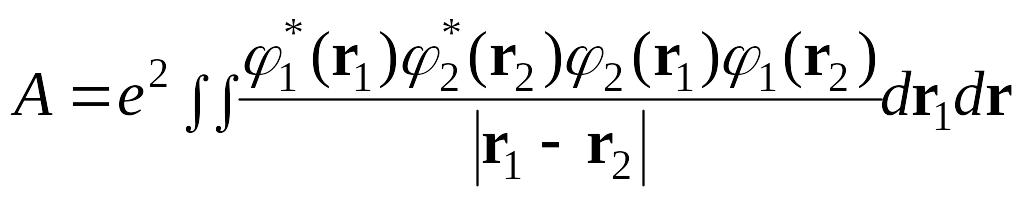Введем плотность заряда в точке 1 и в состоянии 1:
.
Аналогично для 2 точки и во втором состоянии:
,
тогда
.
Мы не можем привести интеграл
к такому же виду. Интеграл
- обменный интеграл. В нем
и
- одно состояние размазано по двум
точкам.
и
- в одной точке имеется два состояния.
Итак
,
.