Московский государственный институт электронной техники (Технический Университет).

А.Г. Фокин

Методы теоретической и математической физики

(конспект лекций для ЭКТ-50М)

2013 г.

Оглавление

Введение. 4

§ 1.1 Вариация и ее свойства. 6

§ 1.2 Уравнение Эйлера. 10

§ 1.3 Функционалы вида 14

§ 1.4 Функционалы, зависящие от производных более высокого порядка 17

§ 1.5 Задача о брахистохроне. 20

§ 1.6 Задача Дидоны. 22

ГЛАВА 2. 25

§2.1 Тензор напряжения и деформации. 25

§2.2 Тензор дисторсии. Тензор деформаций. 26

§2.3 Тензор напряжений. 27

§2.4 Закон Гука. 28

§2.5 Тензор модулей упругости изотропной среды. 30

ГЛАВА 3. 32

§3.1 Интегральные операторы в квантовой механике. 32

§3.2 Интегральный оператор канонического преобразования. 33

§3.3 Каноническое преобразование оператора. 35

§3.4 Унитарные инварианты в квантовой механике. 36

§3.5 Матричная форма задачи о линейном гармоническом осцилляторе (ЛГО). Матричные элементы операторов в методе Шредингера и Гайзенберга (энергетическое представление). 38

§3.6 Уравнение Паули 40

§3.7 Обменное взаимодействие 42

§3.8 Основное состояние атома гелия. 45

ФАКУЛЬТАТИВ 49

§1 Упругие волны в изотропной среде. 49

§2 Тензорная функция Грина волнового уравнения. 50

§3 Уравнение состояния квантового идеального газа. Обменные эффекты. 53

§4 Расчет параметров вырожденного электронного газа. 56

§5 Вырожденный Бозе-газ – квазиклассическое приближение. 59

§6 Плотность вероятности для энергии системы, описываемой каноническим распределением Гиббса. 63

§7 Аппроксимация Гауссовым законом распределения вероятностей для экстенсивного термодинамического параметра. 65

§8 Статистическое описание флуктуаций интенсивного термодинамического параметра. 66

§9 Случай нескольких термодинамических параметров. 68

§10 Многомерное Гауссово распределение. 70

§11 Расчёт флуктуаций термодинамических величин. 71

§12 Расчет термодинамических величин вырожденного Бозе-газа. 72

§13 Расчёт основных термодинамических величин фотонного газа. 76

§14 Метод (представление) Шредингера. Оператор эволюции и его свойства. 78

§15 Метод (представление) Гайзенберга. Уравнение движения для оператора. 79

§16 E – представление. 81

§17 Уравнение Шредингера в матричной форме. 82

§18 Энергетическое представление в случае дискретного спектра: волновая функция, оператор и их свойства. 83

§19 Энергетическое представление в случае дискретного спектра: методы Шредингера и Гайзенберга. 86

§20 Операторы рождения и уничтожения в задаче о ЛГО (линейном гармоническом осцилляторе). 88

§21 Свойства оператора рождения и уничтожения. 89

§22 Волновая функция в - представлении. 91

§23 Оператор f в - представлении. 94

§24 Операторы рождения и уничтожения частиц. 97

§25 Схема Юнга квантовой механики. 99

Глава 1. Введение.

Наряду с задачами, в которых необходимо определить максимальные и минимальные значения некоторой функции в задачах физики нередко возникает необходимость найти максимальные или минимальные значения величин особого рода, называемых функционалами.

Ф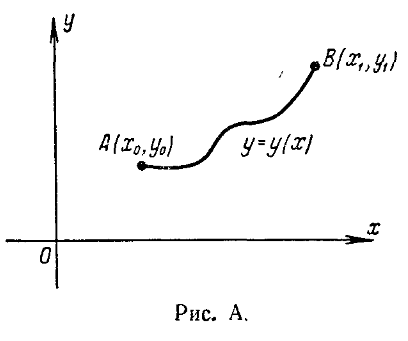 ункционалами называются переменные величины, значения которых определяются выбором одной или нескольких функций. Например, функционалом является длина дуги плоской (или пространственной) кривой, соединяющей две заданные точки и (см. рис. А). Величина может быть вычислена, если задано уравнение кривой ; тогда

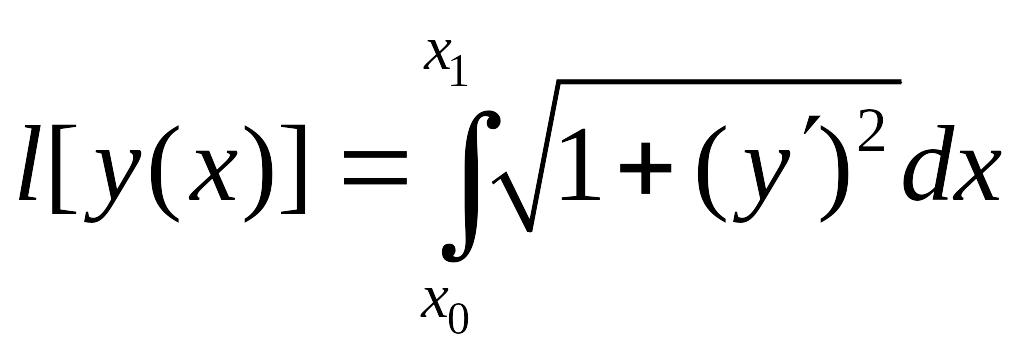
Площадь некоторой поверхности также является функционалом, так как она определяется выбором поверхности, т. е. выбором функции , входящей в уравнение поверхности . Как известно,

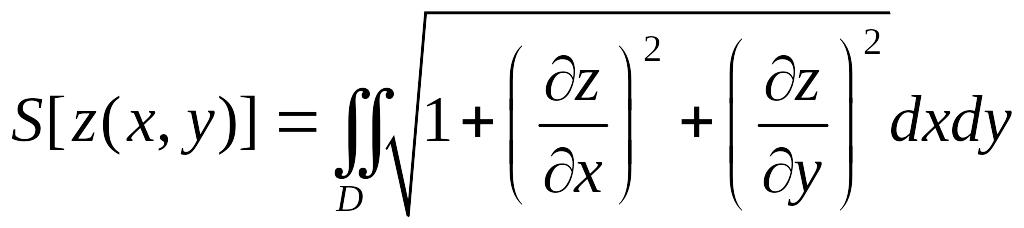
где D — проекция поверхности на плоскость Оху.

Моменты инерции, статические моменты, координаты центра тяжести некоторой однородной кривой или поверхности также являются функционалами, так как их значения определяются выбором кривой или поверхности, т. е. выбором функций, входящих в уравнение этой кривой или поверхности.

В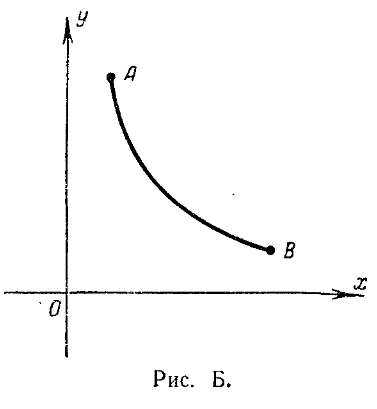 о всех этих примерах мы имеем характерную для функционалов зависимость: функции (или вектор - функции) соответствует число, в то время как при задании функции числу соответствовало число.

Вариационное исчисление изучает методы, позволяющие находить максимальные и минимальные значения функционалов. Задачи, в которых требуется исследовать функционал на максимум или минимум, называются вариационными задачами.

Многие законы механики и физики сводятся к утверждению, что некоторый функционал в рассматриваемом процессе должен достигать минимума или максимума. В такой формулировке эти законы носят название вариационных принципов механики или физики.

К числу таких вариационных принципов или простейших следствий из них принадлежат: принцип наименьшего действия, закон сохранения энергии, закон сохранения импульса, закон сохранения количества движения, закон сохранения момента количества движения, различные вариационные принципы классической и релятивистской теории поля, принцип Ферма в оптике, принцип Кастилиано в теории упругости и т. д.

Вариационное исчисление начало развиваться с 1696 года и оформилось в самостоятельную математическую дисциплину с собственными методами исследования после фундаментальных работ действительного члена Петербургской Академии наук Л. Эйлера (1707 —1783 г.), которого с полным основанием можно считать создателем вариационного исчисления.

Большое влияние на развитие вариационного исчисления оказали следующие три задачи:

Задача о брахистохроне. В 1696 году Иоганн Бернулли опубликовал письмо, в котором предлагал вниманию математиков задачу о линии быстрейшего ската — брахистохроне. В этой задаче требуется определить линию, соединяющую две заданные точки А к В, не лежащие на одной вертикальной прямой, и обладающую тем свойством, что материальная точка скатится по этой линии из точки А в точку В за кратчайшее время (рис. Б).

Легко видеть, что линией быстрейшего ската не будет прямая, соединяющая точки А и В, хотя она и является кратчайшим расстоянием между точками А и В, так как при движении по прямой скорость движения будет нарастать сравнительно медленно; если же мы возьмем кривую, более круто спускающуюся около точки А вниз, то хотя путь и удлинится, но значительная часть пути будет пройдена с большей скоростью. Решение задачи о брахистохроне было дано И. Бернулли, Я. Бернулли, Г. Лейбницем, И. Ньютоном и Г. Лопиталем. Оказалось, что линией быстрейшего ската является циклоида.

З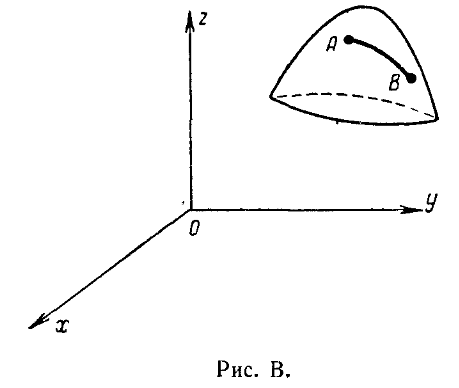 адача о геодезических линиях. Требуется определить линию наименьшей длины, соединяющую две заданные точки на некоторой поверхности (рис. В). Такие кратчайшие линии называются геодезическими.

Мы имеем типичную вариационную задачу на так называемый связанный или условный экстремум. Необходимо найти минимум функционала

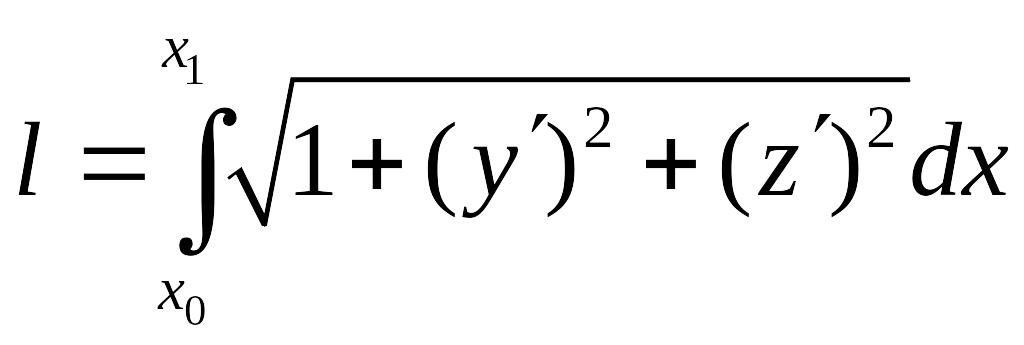
причем функции и должны быть подчинены условию . Эта задача была решена в 1698 году Я. Бернулли, но общий метод решения задач такого типа был дан лишь в работах Л. Эйлера и Ж. Лагранжа.

Изопериметрическая задача. Требуется найти замкнутую линию заданной длины , ограничивающую максимальную площадь . Такой линией, как было известно еще в древней Греции, является окружность. В этой задаче требуется определить экстремум функционала при наличии своеобразного дополнительного условия — длина кривой должна быть постоянна, т. е. функционал

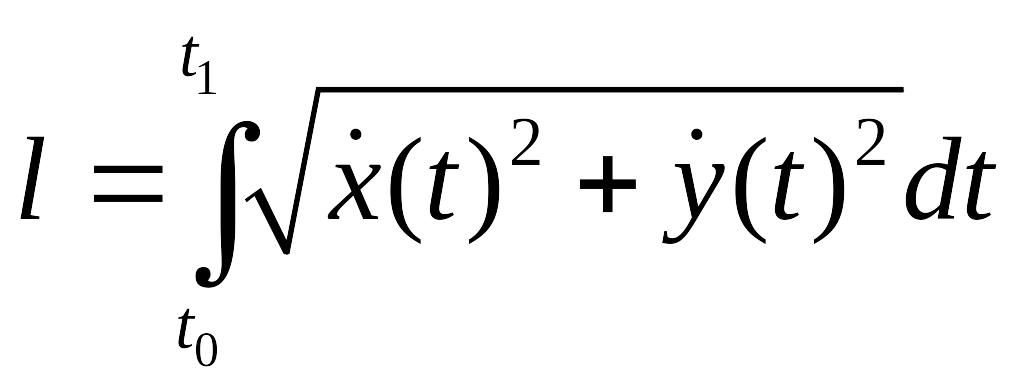
сохраняет постоянное значение. Условия такого типа называются изопериметрическими. Общие методы решения задач с изопериметрическими условиями были разработаны Л. Эйлером.