Перевод целых чисел из десятичной системы в любую другую позиционную систему счисления

При переводе целого десятичного числа в систему с основанием q его необходимо последовательно делить на q до тех пор, пока не останется остаток, меньший или равный q–1. Число в системе с основанием q записывается как последовательность остатков от деления, записанных в обратном порядке, начиная с последнего.

Пример 2. Перевести число 75 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:

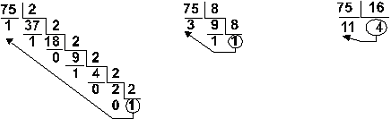
Ответ: 75₁₀ = 1 001 011₂ = 113₈ = 4B₁₆.

Особенности использования восьмеричной и шестнадцатеричной систем счисления. Двоичная система, удобная для компьютеров, для человека неудобна из-за ее громоздкости и непривычной записи.

Перевод чисел из десятичной системы в двоичную и наоборот выполняет машина. Однако, чтобы профессионально использовать компьютер, следует научиться понимать слово машины. Для этого и разработаны восьмеричная и шестнадцатеричная системы.

Числа в этих системах читаются почти так же легко, как десятичные, требуют соответственно в три (восьмеричная) и в четыре (шестнадцатеричная) раза меньше разрядов, чем в двоичной системе (ведь числа 8 и 16 – соответственно, третья и четвертая степени числа 2).

Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему очень прост: достаточно каждую цифру заменить эквивалентной ей двоичной триадой (тройкой цифр) или тетрадой (четверкой цифр).

Пример 3.

Чтобы перевести число из двоичной системы в восьмеричную или шестнадцатеричную, его нужно разбить влево и вправо от запятой на триады (для восьмеричной) или тетрады (для шестнадцатеричной) и каждую такую группу заменить соответствующей восьмеричной (шестнадцатеричной) цифрой.

Пример 4.

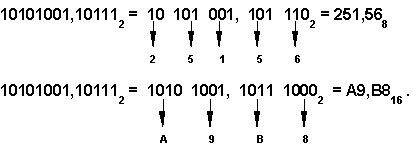
Перевод дробной части числа из десятичной системы в любую другую позиционную систему счисления. Для перевода дробной части десятичного числа необходимо последовательно умножать ее (только дробную часть), на основание новой системы счисления q до тех пор, пока не будет достигнута заданная точность перевода. Число в системе с основанием q записывается как последовательность целых частей полученных в ходе преобразования произведений, записанных в прямом порядке их получения.

Пример 5. Перевести число 0,47₁₀ из десятичной системы в двоичную, восьмеричную с точностью в пять разрядов.

0 47 0 47

x 2 x8

0 94 3 76

x 2 x8

1 88 6 08

x 2 x8

1 76 0 64

x 2 x8

1 52 5 12

x 2 x8

1 04 0 96

0,47₁₀  0,01111₂ 0,47₁₀  0,3605₈

Проверка: 0,01111₂ = 0*2^-1+1*2^-2+1*2^-3+1*2^-4 = 0,25 + 0,125 + 0,0625 + + 0,03125 = 0,46875;

0,3605₈ = 3*8^-1 + 6*8^-2 + 5*8^-4 = 0,375 + 0,09375 + 0,0012  0,46997

Попутно заметим, что в десятичной системе счисления правильная дробь переводится в десятичную дробь в конечном виде только в том случае, если ее знаменатель в качестве множителей имеет только степени двоек и пятерок, т.е. дробь имеет вид .

Все же остальные дроби переводятся в бесконечные периодические дроби. Аналогично в двоичной системе счисления конечный вид получают дроби, где в знаменателе только степени двойки, т.е. большинство десятичных конечных дробей в двоичной системе счисления будут бесконечными периодическими дробями.

Если ведутся приближенные вычисления, то последний разряд является сомнительным и для обеспечения в приближенных вычислениях одинаковой точности в двоичной и десятичной записях числа без бесконечных дробей достаточно взять число двоичных разрядов в 4 раза (log₂10 ≈ 3,3) больше, чем десятичных.

Представление чисел в ЭВМ. В ЭВМ применяются две формы представления чисел:

• естественная форма, или форма с фиксированной запятой (точкой)  ФЗ (ФТ);

• нормальная форма, или форма с плавающей запятой (точкой)  ПЗ (ПТ).

Фиксированная запятая (точка). В форме представления с фиксированной запятой (точкой) числа изображаются в виде последовательности цифр с постоянным для всех чисел положением запятой, отделяющей целую часть от дробной.

Например, пусть числа представлены в десятичной системе счисления и имеют пять разрядов в целой части числа (до запятой) и пять в дробной части (после запятой). Числа, записанные в такую разрядную сетку, имеют вид:

+03221,45610

+00000,00014.

71202,40260.

Эта форма наиболее проста, естественна, но имеет небольшой диапазон представления чисел и поэтому чаще всего неприемлема при вычислениях.

Диапазон значащих чисел N в системе счисления с основанием Р при наличии m разрядов в целой части и s разрядов в дробной части числа (без учета знака числа) будет таким:

P^-s N  P^m  P^-s.

Например, при Р=2, m = 10 и s = 6 числа изменяются в диапазоне 0,015 < N< 1024. Если в результате операции получится число, выходящее за допустимые пределы, произойдет переполнение разрядной сетки, и дальнейшие вычисления теряют смысл. В современных компьютерах естественная форма представления используется как вспомогательная и только для целых чисел.

В памяти ПК числа с фиксированной точкой хранятся в трех форматах:

а) полуслово  это обычно 16 бит, или 2 байта;

б) слово  32 бита, или 4 байта;

в) двойное слово – 64 бита, или 8 байтов. Отрицательные числа с ФТ записываются в разрядную сетку в дополнительных кодах, которые образуются прибавлением единицы к младшему разряду обратного кода. Обратный код получается заменой единиц на нули, а нулей на единицы в прямом двоичном коде (подробнее см. § 2.2).

Плавающая запятая (точка). В форме представления с плавающей запятой (точкой) число изображается в виде двух групп цифр:

• мантисса;

• порядок.

При этом абсолютная величина мантиссы должна быть меньше 1, а порядок должен быть целым числом. В общем виде число в форме с плавающей запятой может быть представлено так:

N=±MxP^±r,

где М  мантисса числа (|М| < 1);

r  порядок числа (целое число);

Р  основание системы счисления.

Например, приведенные ранее числа в нормальной форме запишутся следующим образом:

+0,322145610 х 10⁺⁴;

+0,14 х 10^-3;

0,7120240260 х 10⁵.

Нормальная форма представления обеспечивает большой диапазон отображения чисел и является основной в современных компьютерах. Так, диапазон значащих чисел в системе счисления с основанием Р при наличии m разрядов у мантиссы и s разрядов у порядка (без учета знаковых разрядов порядка и мантиссы) будет:

Например, при Р = 2, m = 22 и s = 10 диапазон чисел простирается примерно от 10^-300 до 10³⁰⁰. Для сравнения: количество секунд, которые прошли с момента образования планет Солнечной системы, составляет около 10¹⁸.

Однако, например, число 4235,25 может быть записано в одном из видов:

4235,25 = 423,525· 10¹ = 42,3525· 10² = 4,23525· 10³ = 0,423525· 10⁴.

Очевидно, такое представление не однозначно. Поэтому следует заметить, что все числа с плавающей запятой хранятся в машине в так называемом нормализованном виде.

Нормализованным называют такое число, старший разряд мантиссы которого больше нуля (0,1 ≤ |M| < 1 для десятичной системы счисления).

Нормализованные, т. е. приведенные к правильной дроби, числа:

24,261₁₀= 0,24261₁₀ х 10⁺²;

0,00007741₈=0,7741₈ х 8^-4;

5A8,2B₁₆=0,5A82B₁₆ x 16⁺³;

В памяти ПК числа с ПТ хранятся в двух форматах:

• слово  32 бита, или 4 байта;

• двойное слово  64 бита, или 8 байт.

Разрядная сетка для чисел с ПТ имеет следующую структуру (рис. 2.1):

• нулевой разряд  это знак числа (0  для положительных, 1  для отрицательных чисел);

• с 1 по 7 разряд записывается порядок в прямом двоичном коде, пустые разряды заполняются нулями. В первом разряде указывается знак порядка (0  «плюс» или 1  «минус»);

• с 8 по 31 (63) указывается мантисса, слева направо без нуля целых в прямом двоичном коде и для отрицательных чисел и пустые разряды заполняются нулями.

Рассмотрим на примере, как записывается некоторое число в нормализованном виде в четырехбайтовом формате с семью разрядами для записи порядка (рис. 2.1).

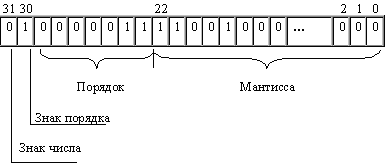
Рис. 2.1. Запись числа в нормализованном виде в четырехбайтовом формате с семью разрядами для записи порядка