1.2 Елементи сучасної теорії погрішностей

При описі багатьох фізичних явищ неможливо прогнозувати точне поводження окремих фізичних подій. Однак їх можна описати, скориставшись поняттями "середнє поводження" чи "ймовірність".

Теорія ймовірностей основана на припущенні, що частота появи окремого результату в процесі експерименту наближається до кінцевої межі. Ймовірність Р(А) деякого результату А дорівнює частоті його появи

, (1.6)

де N- загальне число дослідів чи спостережень; n(N) - число появ A під час цих дослідів.

У фізиці часто ймовірність можна визначити трохи інакше:

, (1.7)

де ∆t - час спостереження результату A; Т - повний час експерименту.

Результат А (випадкова величина, тобто для її появи неможливо знайти причину чи причин занадто багато і їх вплив важко врахувати) може мати як дискретне значення, так і приймати нескінченно багато близьких значень (неперервний спектр). В останньому випадку характерна особливість: імовірність окремої події, що полягає в тому, що виникає саме результат А (певне значення) дорівнює нулю (близька до нуля). Тому можна говорити лише про ймовірність того, що випадкова величина може знаходитися в інтервалі ∆Х значень від Х до X+∆Х. Ймовірність d(X) того, що випадкова величина приймає значення від Х до X+dХ, залежить від самого Х, (тобто є деякою функцією f(X)) і від величини .

Сукупність усіх значень ймовірностей даної величини утворює розподіл даної випадкової величини f(Х). Ця функція розподілу ймовірності показує, як розподіляється ймовірність на d в залежності від Х:

, (1.8)

і

Рисунок 1.1 - Графік функції розподілу ймовірності в залежності від Х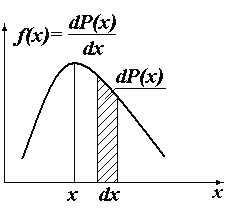

часто називається густиною ймовірності (рис.1.1). Звичайно f(X) виражається у вигляді графіка, з якого можна судити про величину dP(X) (площа заштрихованої ділянки).

Значення випадкової величини, що відповідає максимуму f(X), називається найімовірнішим.

В теорії ймовірностей і її додатків важливу роль відіграє диференціальний закон розподілу густини ймовірності випадкової величини, що має вигляд:

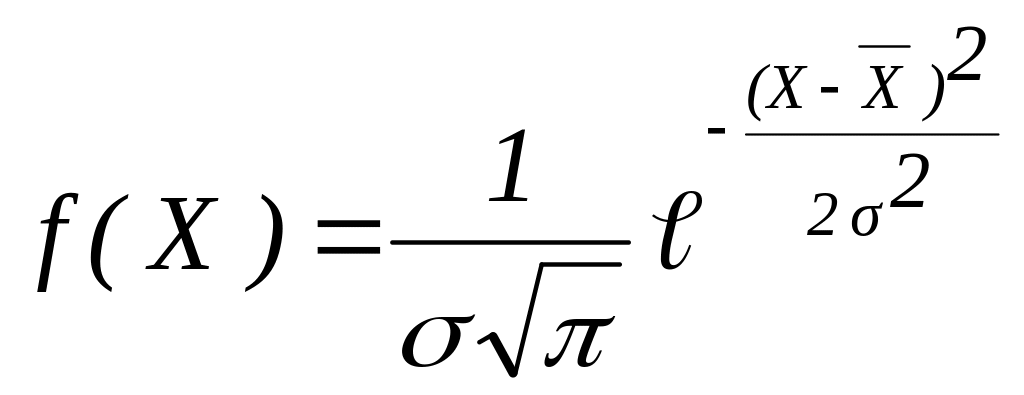
для дискретного ряду величин, де - середнє значення чи математичне очікування

,

- для випадкової величини, неперервно розподіленої (Х змінюється неперервно);

σ² - дисперсія випадкової величини.

Якщо

,

тоді

.

Це середнє квадратичне відхилення називається дисперсією випадкової величини. Дисперсія визначає гостроту кривої f(Х). Форма кривих Гаусса (нормальний закон розподілу) представлена на рис.1.2 (для різних значень дисперсії).

Рисунок 1.2 - Форма кривих Гауса

для різних значень дисперсії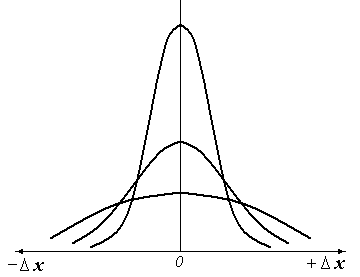

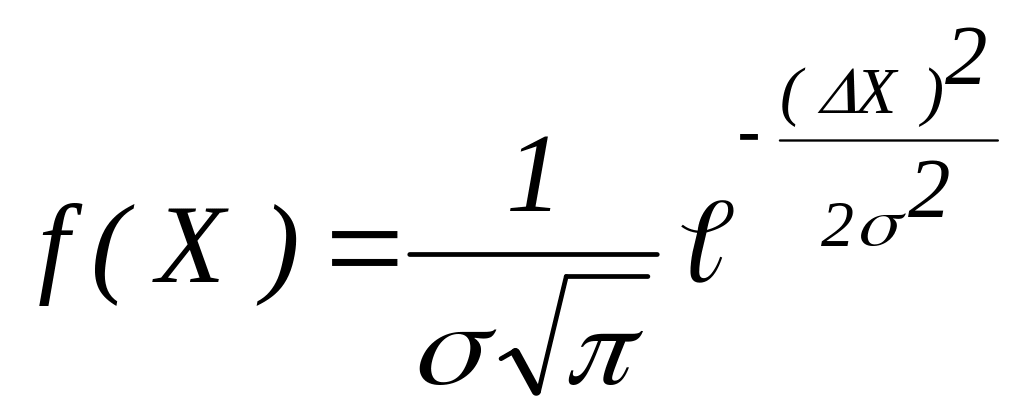При вимірюваннях фізичних величин у тих випадках, коли основну роль відіграють випадкові помилки, всі оцінки точності вимірювання можна зробити тільки з деякою ймовірністю. Для того, щоб виявити випадкову помилку вимірювань, їх необхідно повторити кілька разів. Якщо кожне вимірювання дає результати, трохи відмінні від інших, випадкова помилка відіграє істотну роль. За найбільш імовірне значення вимірюваної величини варто прийняти її середнє арифметичне значення за умови, що при великому числі вимірювань помилки однакової величини, але різного знака - рівноймовірнісні. Якщо помилки можуть приймати неперервний ряд значень і частота появ помилок зменшується зі збільшенням помилки при рівноточних (з однаковою старанністю проведених) вимірюваннях, то крива розподілу випадкових погрішностей описується кривою Гауса (нормальний закон розподілу випадкових величин):

,

де ∆X - величина випадкової похибки, ймовірність якої оцінюється f(X)=Y.

Отже, для характеристики похибки необхідно знати величину похибки ∆Х (∆Х називають довірчим інтервалом) і величину ймовірності того, що результат вимірювань характеризується даною погрішністю ∆Х (довірча імовірність або коефіцієнт надійності ). Вказівка однієї похибки без коефіцієнта надійності не має сенсу.

Для одержання чисельних результатів застосовуються таблиці нормального розподілу густини ймовірності, але щоб ними скористатися, необхідно нормувати f(X)

,

де - довірчий інтервал, виражений у частках середньої квадратичної помилки.

Нормована функція нормального розподілу імовірності

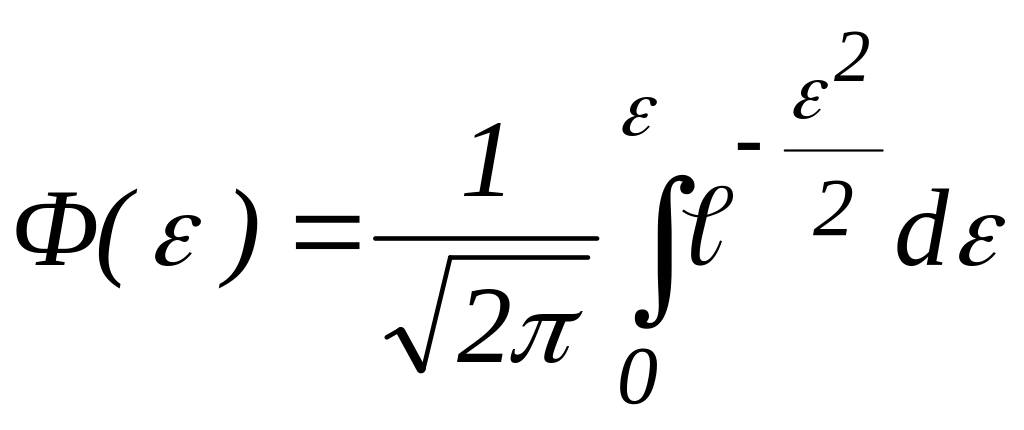
є функцією Лапласа (інтеграл ймовірностей). Так, наприклад, середній квадратичній помилці відповідає довірча імовірність 0,68 (=1), подвоєній середній квадратичній помилці (2) - довірча імовірність 0,95 (або 95 %) і т.д.

Часто, указуючи для оцінки похибки величину σ, не дають значення довірчої ймовірності, вважаючи її відомою величиною (68%).

Припустимо, вимірювана величина Z є сумою (чи різницею) Х і У, результати вимірювання яких незалежні, - їхні дисперсії, тоді

.

Отже, для знаходження сумарної помилки потрібно складати не самі помилки, а їхні квадрати (S_Z - середня квадратична помилка суми).

Нехай Х₁, Х₂, Х₃..., Х_n - результати окремих вимірювань, причому кожне з них характеризується однією і тією же дисперсією S. Середнє з них

.

Дисперсія ,

.

Отже,

.

Тоді середня квадратична похибка S_Y середнього арифметичного Y дорівнює середній квадратичній похибці окремого результату, поділеній на корінь квадратний з числа вимірювань. Тобто, збільшуючи кількість вимірювань, можна значно зменшити похибку, не покращуючи точність (зменшення S чи σ, що визначається методикою вимірювань). Нормальний закон розподілу випадкових погрішностей добре виконується при досить великій кількості вимірювань (кілька сотень) і дозволяє оцінити його параметри: σ² для заданого ∆Х, чи ∆Х по заданому σ².

Якщо ж число вимірювань невелике (менше двадцяти), то ці задачі можна вирішити, скориставшись іншим законом розподілу ймовірностей випадкових величин - розподілом Стьюдента:

,

де ;

∆X - абсолютна похибка результату серій вимірювання;

σ - середньоквадратична похибка результату тієї ж серії вимірювань;

Г(n) – гама функція.

При n→ (n→20) цей розподіл переходить у розподіл Гауса.

При малій серії вимірювань для розрахунку ∆Х при заданій надійності  використовують коефіцієнт Стьюдента t_, що залежить від кількості вимірювань n і величини  :

, (1.9)

де 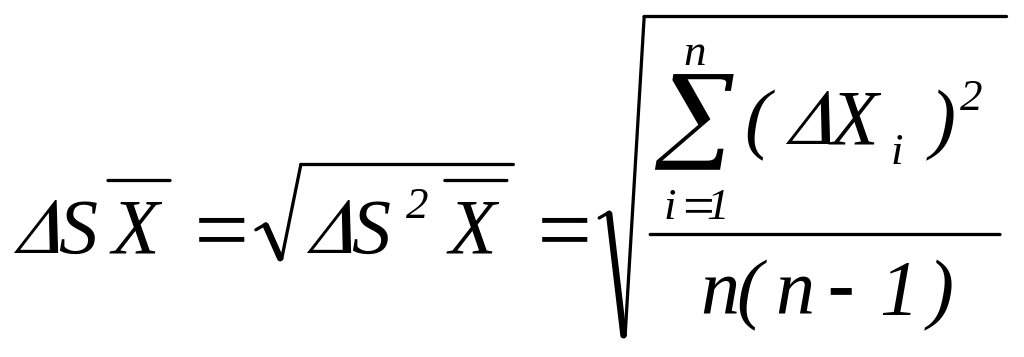- середньоквадратична похибка результату серій вимірювань.

Задаючи надійність, тобто припускаючи  рівним певній величині, за числом вимірювань n знаходимо в таблиці значення коефіцієнта Стьюдента. Визначивши ∆S , знаходимо ∆X:

. (1.10)

Результат можна записати у вигляді

. (1.11)

На закінчення пропонується зразковий порядок операцій для оцінки похибки прямих вимірювань.

1. Обчислюється середнє значення з n вимірювань:

.

2. Знаходяться похибки окремих вимірювань:

.

3. Обчислюються квадрати погрішностей окремих вимірювань (∆X_i)².

4. Якщо є вимірювання, що відрізняються різко за своїм значенням від інших, перевірити чи не є вони промахами.

5. Знаходять середню квадратичну похибку серії вимірювань

.

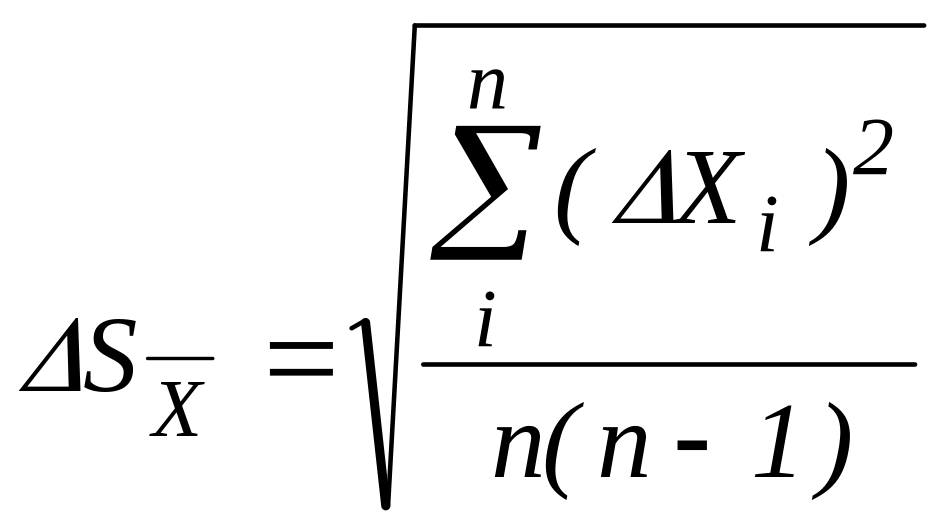6. Задається коефіцієнт надійності .

7. Визначається коефіцієнт Стьюдента t_(n) для даного n і  за таблицею.

8. Знаходять межі довірчого інтервалу (похибка результату вимірювань)

.

9. Записується остаточний результат: .

10. Визначається відносна похибка серії вимірювань - величина, що характеризує точність вимірювань

.

1.3 Математична обробка результатів досліду

Часто в результаті досліду зв'язок між деякими величинами виявляється у вигляді таблиці, у якій для кожного значення Х, при якому проводилось вимірювання (умови досліду), поставлене відповідне значення Y, знайдене шляхом вимірювань. Задані так функції можуть далі, наприклад, диференціюватися, інтегруватися, можуть знадобитися значення функції при проміжних, не вписаних у таблицю, значеннях незалежної змінної (задачі інтерполяції) чи при значеннях незалежної змінної, що знаходяться за межами таблиці (задача екстраполяції).

Для вирішення цих задач зручніше скористатися математичною залежністю між Х і Y, заданою у вигляді формули. Формулу, підібрану за експериментальними даними, називають емпіричною формулою. Формула тим ліпша, чим більше теоретичних уявлень вкладено в неї. Спочатку задаються видом формули, потім, скориставшись результатами сталих величин, що входять у формулу.

Перед тим, як приступити до підбора формули, необхідно нанести дослідні дані на графік, після чого на око, від руки провести через отримані точки найбільш правдоподібну криву. При цьому відразу виявляються ті дані, в яких можна підозрювати великі помилки. Дуже важливо при проведенні кривої, крім експериментальних точок, використовувати загальні розуміння про те, як повинна поводитися крива при значеннях аргументу, близьких до нуля, при дуже великих значеннях аргументу, поблизу початку координат, біля координатних осей (чи торкається їх, чи перетинає їх і т.п.).

Коли попередня робота проведена й обрано вид формули, можна визначити сталі коефіцієнти. Це роблять за допомогою методу найменших квадратів [1,2,5], однак він приводить до досить громіздких обчислень, особливо коли шукані параметри входять не лінійно. Тому в практичній роботі найчастіше більш ефективними виявляються графічні методи підбору формул.

Пряма лінія займає надзвичайний стан у графічному методі і надійно проводиться за даними точкам. Рівняння прямої лінії має вигляд:

, (1.12)

де числа k і b мають простий геометричний зміст: b - величина відрізка, що відтинається на осі Y, k - тангенс кута нахилу прямої до осі Х. Отже, побудувавши графік, ми визначимо b і k.

Велика перевага графічного методу зв'язана з його наочністю. Якщо експериментальні точки лягають на пряму, за винятком окремих точок, що випали, то ці точки наочно і можуть бути перевірені особливо ретельно. Якщо експериментальні точки не лежать на прямій, то це також видно з графіка. У цьому випадку залежність між Х і Y більш складна, ніж .

Як же підібрати константи, що входять у формулу, якщо вона має більш складний вид, ніж пряма?

Загальна ідея графічного методу полягає в тому, що треба ввести нові змінні так, щоб у цих змінних залежність, що нас цікавить, ставала лінійною. Тому метод іноді називають методом лінеаризації графіка чи просто методом вирівнювання.

Наприклад, часто зустрічається залежність виду .

Розділивши всі члени на Х:

,

і поклавши , одержуємо лінійну залежність Z від Х. Або нехай . Логарифмуючи праву і ліву частини , і ввівши нові змінні Z=lg і t=lg одержимо . З графіка Z(t) легко знайдемо a і n.

Нехай . Логарифмуючи, одержимо , і вибираючи Z=ln, одержимо в координатах Z і Х пряму .

В усіх цих прикладах ми після вибору виду формули вводили змінні так, щоб залежність між цими новими змінними була лінійною. Однак, якщо в нових змінних експериментальні точки не лягають на пряму, те це значить, що вид формули обраний невдало і для опису експериментальних даних треба підібрати формулу іншого виду.

Якщо немає теоретичних засад для підбора формули, звичайно вибирають функціональну залежність з числа найбільш простих, порівнюючи їхні графіки з графіками заданої функції. Через те, що подібність графіків визначена грубо, на око, потрібно, вибравши формулу, перш ніж визначати значення параметрів, перевірити можливість її застосування методом вирівнювання. Вказівки для вирівнювання найпростіших формул дані в [4].

Якщо емпіричну формулу відшукати не вдається, то часто бувають корисні операції безпосереднього графічного інтегрування, диференціювання, графічний розв`язок рівнянь та ін.

На закінчення необхідно відзначити, що при дослідженні багатьох технічних і наукових питань у даний час широке застосовується моделювання різних об'єктів чи явищ. У залежності від характеру дослідження моделювання може бути фізичним або математичним.

У випадку фізичного моделювання дослідження проводиться на моделі, фізично однорідної з об'єктом - оригіналом, що відрізняється від нього тільки кількісно. Таке моделювання дає можливість розширити відомості про явища, що відбуваються в оригіналі.

У випадку математичного моделювання дослідження виконується на моделі, що відтворює фізично інше явище, описуване, однак, такими ж рівняннями, як і явище в оригіналі. У цьому випадку моделюється не конкретний фізичний процес, а певна математична залежність. Цей вид моделювання є основою для створення різних обчислювальних пристроїв.

1.4 Порядок виконання роботи

1. Отримати від викладача 3 екземпляри резисторів.

2. Ознайомитися з роботою мультиметра у режимі вимірювання опору. Навести значення абсолютних похибок.

3. Провести вимірювання опорів резисторів. Вимірювання повторити 10 разів.

4. Ознайомитися з процесом вимірювання лінійних розмірів за допомогою штангенциркуля і мікрометра. Навести значення абсолютних похибок цих приладів.

5. Провести вимірювання геометричних параметрів резисторів: довжини , діаметру . Вимірювання повторити 10 разів.

6. Визначити абсолютні і відносні похибки прямих вимірювань опору, довжини і діаметру резистора.

7. Навести формули для визначення похибки опосередкованих вимірювань наступних величин: , , , , , .

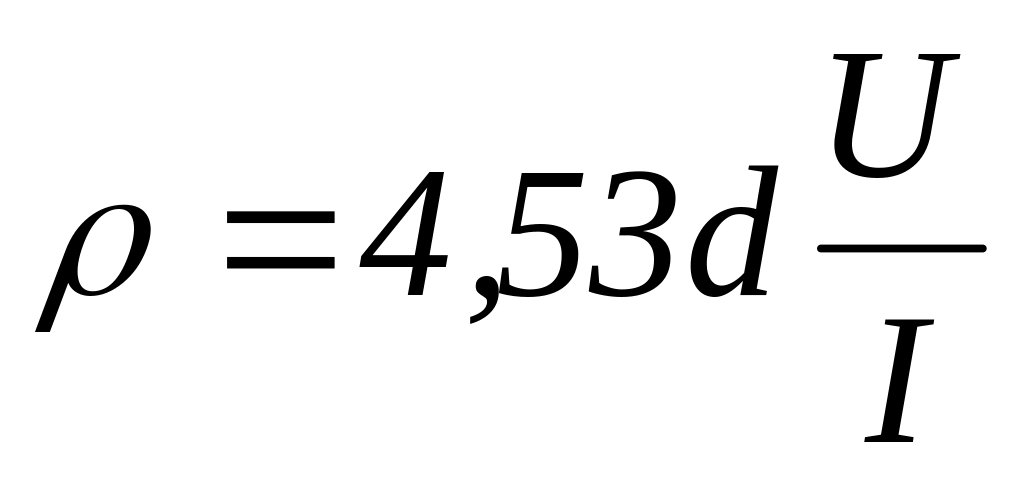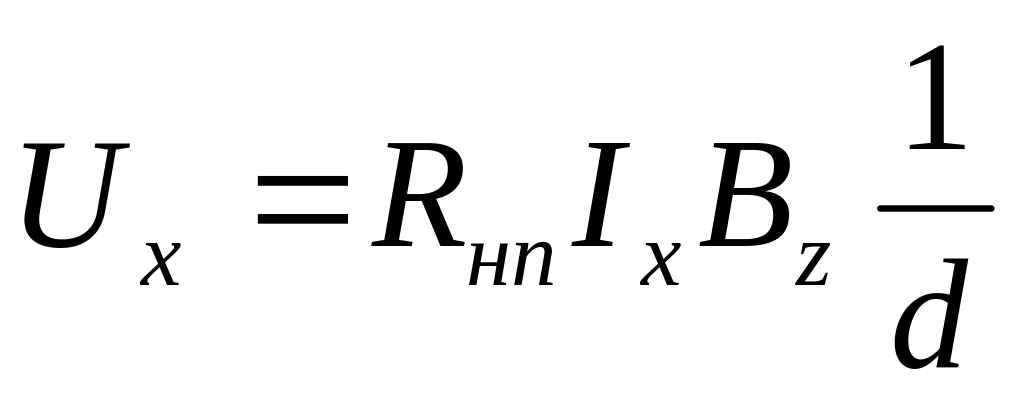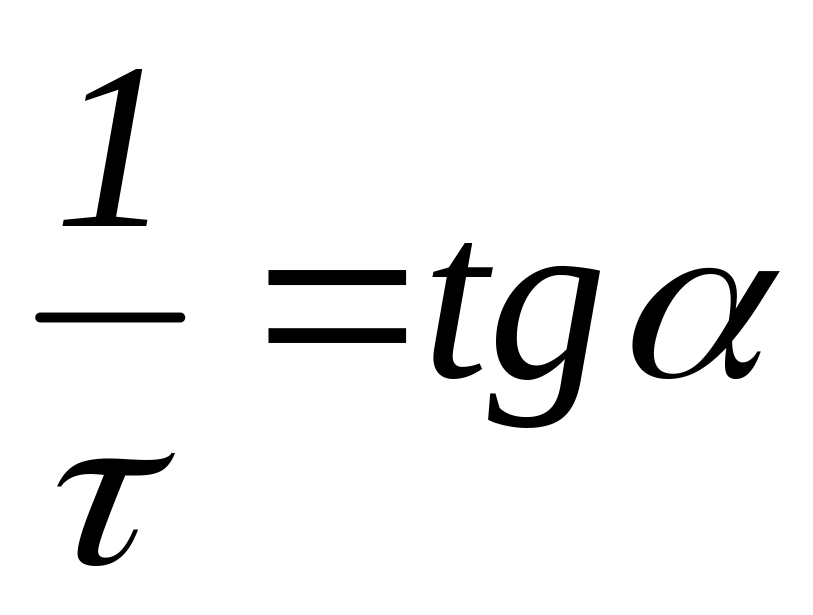8. Визначити похибку вимірювання питомого опору

1.5 Зміст звіту

Звіт повинен містити:

• короткі відомості з теорії похибок, визначення похибки прямих і опосередкованих вимірювань;

• таблицю проведених вимірювань величин , і ;

• обчислити похибки вимірювань, результати занести до таблиці;

• висновки.

1.6 Контрольні запитання

1. В чому полягає причини наявності похибок вимірювання?

2. Що таке промахи, систематичні і випадкові похибки.

3. Як знайти абсолютну похибку окремих вимірювань за великої і малої серії вимірювань?

4. Чому дорівнює абсолютна погрішність вимірювальних приладів?

5. Чому дорівнює погрішність прямих вимірювань?

6. Чому дорівнює погрішність опосередкованих вимірювань?

7. У чому полягає суть математичної обробки результатів досліду?

8. Що таке лінеаризація графіка?