Примеры дифференцирования функций

Пример 1. Продифференцировать функцию .

Решение.

Пример 2. Найти производную функции

Решение.

Пример 3. Продифференцировать функцию .

Решение.

Пример 4. Найти производную сложной функции .

Решение. Согласно правилу дифференцирования сложной функции, находим

Пример 5. Найти производную функции .

Решение.

.

Исследование функции с помощью производной

Производная позволяет решать многочисленные и очень разнообразные задачи не только в математике. Как сказал в своё время И. Кант: «Зрелость науки обычно измеряется тем, в какой мере она использует математику».

Рассмотрим применение производной для исследования функции на монотонность и экстремумы.

Определение:

К ритическими точками функции называются точки, в которых производная равна 0 или не существует.

Критические точки
Производная равна 0 у' = 0	Производная не существует

Примеры вычисления критических точек:

1. у =

1. находим производную: у' =

2. найдём точки, в которых производная равна 0: = 0. 56х = 0, х = 0

3. найдём точки, в которых производная не существует (знаменатель дроби равен 0)

х² -25=0, х = ±5

Ответ: Крит. точки: х = 0, х = ±5

1. у =

1. у′=

2. =0, 68х=0, х=0

3. Знаменатель дроби не равен 0 ни при каких «х»

Ответ: Крит. точки: х = 0

3.у =

1. у′ = .

2. = 0. = 0, lnx = 1, x = e¹, x = e.

3. = 0, lnx = 0, x = e⁰ =1, x = 1.

Ответ: х = 1, х = е.

Исследование функции на монотонность

Исследовать функцию на монотонность – это значит найти такие значения аргумента, при которых функция возрастает или убывает.

Условие монотонности функции:

Если производная функции на некотором промежутке положительна, то функция возрастает на этом промежутке; если производная отрицательна, то функция убывает.

у ′(х)	+	-
у (х)	↑	↓

Исследование функции на экстремумы

Слово «экстремум» - латинское, в дословном переводе означает «крайний, крайность». В математике используется в смысле максимальный, минимальный.

Исследовать функцию на экстремумы – это значит выяснить:

1.есть экстремумы или нет;

2.если есть, то в каких точках;

3 .какой экстремум – из всех возможных, тоаксимум или минимум;

4 .чему равен.

Первое правило нахождения экстремумов:

Если у′ (x0) = 0 и у′(х) при переходе через х0 меняет знак с «+» на «–», то х0 – точка максимума, Если у′ (x0) = 0 и у′(х) при переходе через х0 меняет знак с «–» на «+», то х0 – точка минимума.

(В «Методе флюксий» (1671г.) Ньютон, говоря об определении наибольших и наименьших значений величин, формулирует так называемый принцип остановки: «Когда величина есть наибольшая или наименьшая из всех возможных, то она в этот момент не течёт ни вперед, ни назад». Отсюда он выводит свое правило: приравнять флюксию (производную) нулю).

Примеры:

Исследовать на монотонность и экстремумы функции:

1) у(х) = 3х²+х³+7.

1.Нахожу область определения функции: D(y)= R или х R или х (-∞;+∞) - различные формы записи того факта, что аргумент функции может принимать в данном случае любые действительные значения.

2.Нахожу производную: у ^′= 6х+3х²

3.Нахожу критические точки функции (у′=0): 3х(2+х) = 0, х = 0, х = - 2

4.Вычисляю знаки производной и делаю выводы:

у ^′ + 0 - 0 +

_________ _________ _________________________

у -2 ↓ 0 ↑ х

max min

max y = y(- 2) = 3*4-8+7 = 11, min y = y(0) = 7

5. Ответ: max y = 4, если х = -2; min y = 7, если х = 0; функция возрастает,

если х Є (-∞; - 2] или х Є [0; +∞) и убывает, если х Є [- 2; 0]

2. у(х) =

1.Область определения: х+2 ≠ 0, х ≠ -2 или

2.

3. Критические точки: =0, х =-5; х =1; х = -2 -(производная не существует) + - . - +

у^′: ______0 ______не сущ.____0__________________

у: ↑ -5 ↓ -2 ↓ 1 ↑ х

max нет min

экстремума

max у = у(-5) = -10, min у = у(1) = 2.

5. Ответ: max у = -10, если х = -5, min у = 2, если х = 1.

Функция возрастает, если и убывает, если

3) у =х³ +х⁵

1. ООФ: R

2. у^′=3x²+5x⁴

3. 3x²+5x⁴=0, x²(3+5x²) = 0, x = 0 – ед.крит. точка.

4. у′: _______+_____0 __________+__________________

у : ^{↑ 0 ↑ х}

нет

экстремума

В точке х = 0 производная равна 0, но не меняет знак, поэтому экстремума в этой точке нет.

5. Ответ: функция возрастает во всей области определения, экстремумов нет.

Производные высших порядков. Точки перегиба.

До сих пор мы рассматривали производную f′(x) от функции f(x), называемую производной первого порядка. Но производная сама является функцией, которая также может иметь производную.

Определение:

П роизводной п-го порядка функции f(x), называется производная от производной

(п -1)-го порядка данной функции.

Обозначение: f″(x) – вторая производная функции f(x).

Для обозначения производных более высокого порядка используются арабские цифры в скобках или римские цифры, например: f⁽⁴⁾(x),...,f⁽ⁿ⁾(x) или f^IV(x) и т.д.

Мы будем использовать только вторую производную.

Примеры:

1. y = ln x, y^′ = 1/x, y^″ = - 1/x², y⁽³⁾ =(- 1/x²)^′ и т.д.

2. у = ,

y^′ = , у″ = =

Определение:

Т очки, в которых вторая производная равна 0 , называются точками перегиба.

Например:

5. Дана функция у = - 3х²+ 6х. Найдите точки перегиба, если они есть.

у′ = - 6х + 6, у″ = - 6, - 6 ≠0, поэтому точек перегиба нет.

2. у =

у′ = ,

= = = .

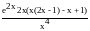=0, 2х²-2х+1=0, Д=4-8=-4<0, корней нет, значит, нет точек перегиба.

3. у = , у′ = = = ,

=0, 10х = 0, х = 0– критическая точка

у″ = = = . -5х²+2х+45 = 0, Д = 4+900 = 904>0-Уравнение имеет 2 корня, значит имеются 2 точки перегиба:

1. у = , ,

,

- 3 + 2ln3x = 0, 2ln3x = 3, ln3x = 3/2, 3x = e^3/2, x = e^3/2/3 = - точка перегиба.

Ранее мы рассматривали точки экстремума, нахождение которых во многом определяет структуру графика функции. Точки перегиба – это «узловые» точки, помогающие более точно построить график.

Имеет место достаточное условие выпуклости функции:

Если вторая производная функции положительна (отрицательна) в некотором промежутке, то функция выпукла вниз (вверх) на этом промежутке.

Графики функций, выпуклых вниз и вверх, изображены на рисунках:

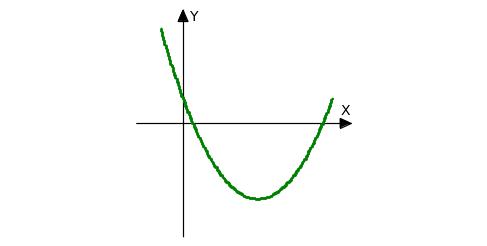
В точке перегиба происходит изменение направления выпуклости. Для лучшего запоминания этого утверждения используют так называемое «правило дождя»:

f″(x)>0	f″(x)<0
Сосуд полон	Сосуд пуст
+	–

Пример:

.

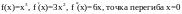График:

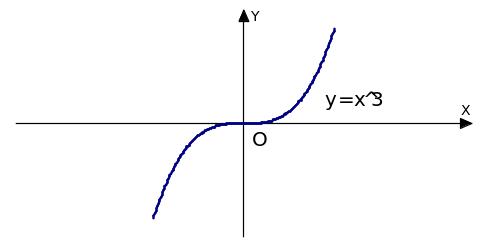
В точке перегиба х = 0 выпуклость вверх меняется на выпуклость вниз. Если провести касательную к графику в точке перегиба, то она разделит график на две части: одна выше касательной, другая – ниже.

Алгоритм исследования функции на выпуклость и точки перегиба:

1. Найти вторую производную функции. 2. Найти точки, в которых вторая производная равна 0. 3. Вычислить знак второй производной слева и справа от найденных точек и сделать вывод об интервалах выпуклости и наличии точек перегиба. 4. Найти значения функции в точках перегиба.

С помощью второй производной также можно исследовать функцию на экстремумы. Дело в том, что не всегда такой вопрос можно решить при помощи первой производной. Тогда выручает вторая производная. Имеет место

второе правило нахождения экстремумов:

Пусть f′(x0) = 0 и f″(x0)>0, то х0 – точка минимума; если f′(x0) = 0 и f″(x0)<0, то х0 – точка максимума.

Например:

1. у = х³ -4.5х²+6х – 2

1.у′ = 3х²- 9х + 6

2. Крит. точки: 3х²- 9х + 6 = 0, х₁ = 1, х₂ =2

3. Знак второй производной в крит. точках: у″=6х – 9, у″(1) = - 3<0, следовательно х₁ = 1 – точка максимума,

у″(2) = 3>0, следовательно х₂ =2 – точка минимума

4.у_max=1³-4.5*1+6*1-2 = 0.5, y_min= y(2) =2³-4.5*2+6*2-2 = 9.

2. Производитель реализует свою продукцию по цене 12 ед., а издержки при этом задаются кубической зависимостью S(x) = 3x + x³. Найти оптимальный для производителя объём выпуска продукции «х» и соответствующую ему прибыль.

1. Составим функцию прибыли: С(х) = 12х-(3х+х³) = 9х- х³.

2. С′(х) = 9 -3х²

3. 9 -3х² = 0, х = ±

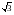
4. (х) = - 6х<0 при любом «х» - х>0-т.к.выражает количество продукции, поэтому

х = ≈2- точка максимума

5. С(2) ≈10.

Ответ: оптимальный объём равен 2, прибыль равна при этом 10.

*Асимптоты графика функции.

Асимптота дословно с греческого переводится как «несовпадающие»

Определение:

А симптотой графика функции называется прямая, к которой график функции при неограниченном удалении от начала координат также неограниченно приближается, но не касается.

По предыдущему курсу математики вам известны некоторые графики, имеющие асимптоты (гипербола). Изображённая гипербола имеет две асимптоты: вертикальную и горизонтальную.

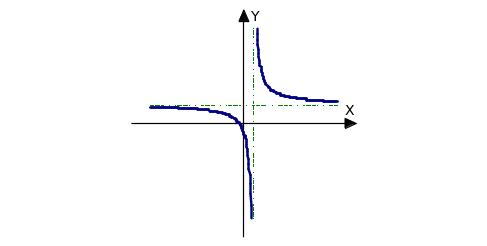
Рассмотрим вопрос об асимптотах более подробно.

Асимптоты бывают:

Вертикальные

Горизонтальные

Наклонные

Определение:

В ертикальной асимптотой называется прямая, имеющая уравнение вида х = а, где «а» – точка, не принадлежащая области определения функции.

Например:

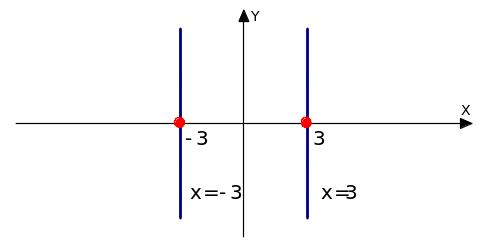
1) у =

D(y): х ≠ ±3, следовательно, х = ± 3 – вертикальные асимптоты.

1. у = D(y): х >1, ln(x-1) ≠ 0, x-1 ≠ 1, x ≠ 2, следовательно, х = 2 – вертикальная асимптота

Определение:

Г оризонтальной асимптотой графика функции y = f(x) называется прямая, имеющая уравнение вида: у =

Например:

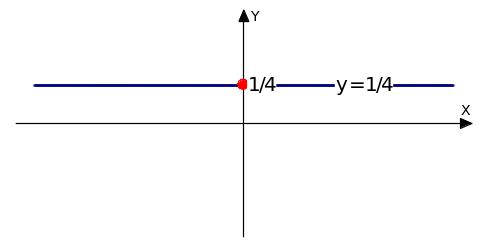
f(x)=

f(x) = = ¼, следовательно, у= ¼-гор. ас.

Определение:

Наклонной асимптотой называется прямая, имеющая уравнение вида у = кх+с, где

Например:

Дана функция y= , рассчитайте её асимптоты.

Решение

1. ООФ: x ≠ 0.5 , следовательно, прямая х = 0.5 – вертикальная асимптота.

2. у = ∞, следовательно, горизонтальной асимптоты нет.

x² +11 x² + 11

к = lim ----------- = lim ------------ = 1/4, следовательно, к =1/4

x→∞ x(4x – 2) x→∞ 4x² - 2x

с = , следовательно, с =

поэтому наклонной асимптотой будет прямая у =

На графике эти асимптоты будут выглядеть так:

*. Схема исследования функции с помощью производной и построение графика.

1.Найти область определения функции.

2.Найти точки пересечения графика с осями координат: с осью х (у=0), с осью у (х=0).

3.Найти производную.

4.Вычислить критические точки (у ^′= 0 и не входящие в область определения).

5.Исследовать функцию на монотонность и экстремумы.

6.Найти вторую производную: у^″= (у^′)^′

7.Вычислить точки перегиба (у ^″= 0)

8. Исследовать на выпуклость

9.Рассчитать асимптоты.

10.Если надо, то вычислить дополнительные точки.

11.Построить график.

Примеры:

1. у = - 2х²+3х+1

1. D(y) = R

2.С осью х: - 2х²+3х+1 = 0 ( потребуются дополнительные точки)

с осью у: у(0) = 1 (0;1)- точка пересечения с осью у.

3. у ^′= х²-4х+3

4. Кр. точки: х²-4х+3 = 0, х = 3, х = 1 (по теореме Виета)

5. Иссл. на монотонность и экстремумы:

у^′: ______+___0_______-_______0________+______________

у: 1 3 х

max min

max y = y(1) = 7/3, min y = y(3) = 1.

6. y^″ = 2х - 4

7. 2х-4 = 0, 2х = 4, х = 2 , (2;5/3) – точка перегиба.

8. Асимптоты: верт. нет, т.к. D=R; limy=∞, поэтому и горизонтальных тоже нет;

x→∞

накл.-? к=limy/x = ∞, поэтому нет и наклонных.

9. Доп. точки: у(-1) = - 13/3, у(4) = 7/3.

10. График (см. рисунок)

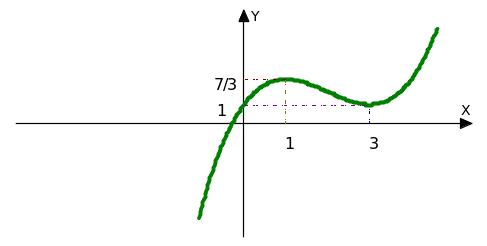
2.

1. ООФ: х ≠ 2

2. Точки пересечения: с осью х: =0, х² +1=0, корней нет, следовательно, с осью х пересечения нет.

С осью у: х=0, у = - ½, следовательно, график пересекает ось у в точке (0; - ½).

3.

4. Крит. точки: =0, х² -4х-1=0, D=16+4=20, х_1,2 =2± , х₃ =2.

5.Исследование на монотонность и экстремумы:

у′: ______+_____0_____-____нет_____-_____0_______+___

у: 2- 2 2+

max нет min

экстремума

max у = у(2- ) =

min у = у(2+ ) = 2 +4

5. у" =

6. Точки перегиба: =0, корней нет, точек перегиба нет.

7. Асимптоты:

а) х =2 – верт. асимптота

б) у = - горизонтальных нет.

в) к =

y = x+2 – наклонная асимптота

5. График:

3. у = х*е^-2х

1. ООФ: х

2. С осью х: х*е^-2х=0, х = 0

с осью у: х = 0, у = 0

3.у'= е^-2х-2х е^-2х = е^-2х(1-2х)

4. Крит.точки: е^-2х(1-2х) = 0, 1-2х=0, х = 0.5

5. Исследование на монотонность и экстремумы:

у': ________________-_______0_____+_____________________

у: 0.5

min

min y = y(0.5) = 0.5*e^-1= ≈ 0.19

6. у" =

7. Точки перегиба: = 0, 1-х = 0, х = 1, у(1) =

8. Исследование на выпуклость:

у": _________-_____________0___+________

у: вып. вверх 1 выпуклость вниз

9. Асимптоты: а) вертикальных нет, т.к. ООФ: х

б)

Следовательно, у = 0 – горизонтальная асимптота, если х → + ∞. Если х → - ∞, то горизонтальных асимптот нет.

в) а =

Это значит, что наклонных асимптот нет.

10. График:

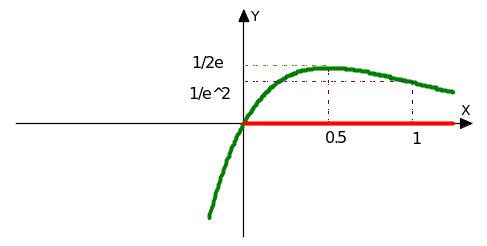
Экономический смысл производной

Из предыдущего курса математики вам известно, что производная имеет геометрический и механический смысл. (Какой?) Но этим значение производной не ограничивается: в приложениях производной отмечается, что она имеет и экономический смысл. Например, производительность труда в данный момент есть производная объёма произведённой продукции по времени:

Z = V′(t)

z – производительность труда, V – объём произведённой продукции

Кроме того, производная позволяет находить скорость и темпы изменения различных экономических показателей:

Первая производная показывает скорость изменения, а вторая производная = скорость изменения скорости = ускорение = темпы изменения.

у′	Показывает, что происходит с изучаемой величиной: увеличивается или уменьшается
у″	Показывает, в каком темпе это происходит

Пример:

Объём продукции на некотором производстве может быть описан формулой . Вычислите производительность труда, скорость её изменения через час после начала работы и за час до её окончания.

Решение

Производительность–это производная объёма

у = , поэтому после первого часа V′(1)=112,5(ед./час), V′(7)=82,5(ед./час). Очевидно, что к концу рабочего дня производительность существенно снизилась. Но это факт понятный и без производной.

Но как конкретно изменяется производительность? Для этого найдём её производную, показывающую, что с ней происходит: у′(t) = - 5t + 15.

- 5t + 15 = 0, t =3

у′________0_____+____0____-_________________________

у 0 ↑ 3 ↓ t

Эта картинка даёт более важную информацию: она говорит о том, что в первые 3 часа работы производительность растёт, а затем убывает.

Как быстро происходит процесс изменения, т.е. в каком темпе она изменяется?

Этот вопрос решается с помощью второй производной:

у″ = - 5 – этот результат говорит о том, что изменение происходит в данном случае в одном темпе. В общем же случае при положительной производной изменение происходит в ускоренном темпе, при отрицательной – в замедленном.

у″	+	−
у	Величина изменяется в ускоренном темпе	Величина изменяется в замедленном темпе

Примеры:

№1:

Опишите темпы изменения издержек, если их зависимость от объёма произведённой продукции описывается формулой: .

Решение

Темпы изменения = ускорение ! Ускорение = вторая производная!

К′ +

К″ 0 – 5 +

Если 0≤х<5, то <0, если х≥5, то >0.

Вывод:

при изменении объёма производства от 0 до 5 издержки растут в замедленном темпе, а при дальнейшем увеличении – растут в ускоренном.

№2: Затраты на производство «х» единиц товара d(x) = 25x+200, цена товара р(х) = 100- .

1. Сколько товара нужно произвести, чтобы прибыль была максимальной? Чему равна максимальная прибыль?

2. Сколько товара нужно произвести, чтобы прибыль была максимальной, если с каждой единицы товара взимается налог, равный 10?

Решение

Прибыль вычисляется по формуле: Q(x) = х*р(х) – d(x) = 100x - - 25x-200 = - +75x -200.

Получаем математическую задачу: найти максимальное значение функции Q(x).

Q′(x) = - +75 = 0, x = 1875.

Q′(x) ̊+ –

0 1875

Q(x). ↑ max ↓

Чтобы прибыль была максимальной, надо произвести 1875 единиц товара.

Величина прибыли: 1875*(100- ) – 25*1875-200 = 70112,5

С учетом налога: Q(x) = х*р(х) – d(x) – 10х. = х*р(х) – 35x – 200 = 100x - - 35х - 200=

=65х - -200, Q′(x) = - +65 =0, х = 1625.

Q′(x) + –

1. 1625 ↓

max

Чтобы прибыль была максимальной при оплате налога, надо произвести 1625 единиц товара.

Ответ: 1) 1875; 70112,5; 2) 1625.

№3: Предприниматель намерен производить и продавать некоторую продукцию. Начальные расходы на организацию дела составят 10000 денежных единиц..Расходы на производство одной единицы продукции зависят от количества произведенной продукции «х» и равны

d(x) = . Цена одной единицы продукции равна р(х) = 3000 – 0.5х. Какое количество продукции нужно произвести, чтобы получить максимальную прибыль? Чему равна максимальная прибыль?

Решение

Очевидно, что общие расходы на производство «х» единиц продукции составляют

D(x) = 10000+x( ) = 10000+2000x+ .

Выручка от продажи «х» единиц продукции составит сумму Р(х) = х(3000 – 0.5х).

Таким образом, прибыль, полученная предпринимателем, составит сумму

Q(x) = P(x) – D(x) = 1000x -0.5x² – 10000- .

Получаем математическую задачу: найти максимальное значение функции Q(x) при х>0 и значение «х», при котором максимум достигается.

Q′(x) = 1000 – х + = 0, преобразую уравнение х²(1000 – х) + 1000 = 0. Традиционно решить это уравнение нам будет затруднительно, поэтому поразмышляем: если х = 1000, то левая часть уравнения положительна, а при х = 1001 – отрицательна. Это значит, что на отрезке [1000;1001] уравнение имеет корень, т.е. есть критическая точка х₀.Т.к. первая производная на [1000;1001] всегда меньше 0, то воспользуемся вторым правилом. Q′(x₀) = 0, Q″(x₀) = -1- <0 и

при любом х>0, х [1000;1001], поэтому х₀ – точка максимума.

Таким образом, для получения максимальной прибыли надо произвести примерно 1000 единиц продукции. При этом максимальная прибыль Q(x) 490000 денежных единиц.