§2. Основные математические методы решения прикладных задач в области профессиональной деятельности

Тот, кто хочет, может достигнуть гораздо большего, чем тот, кто может.

Не пропускай занятий - получишь бонус!

К числу наиболее интересных математических задач относятся задачи на максимум и минимум. Это связано в первую очередь с тем, что в процессе трудовой деятельности люди стремятся наилучшим образом использовать материальные и трудовые ресурсы и при заданном объёме производства свести к минимуму (минимизировать) затраты или при заданных ресурсах обеспечить максимальный выпуск продукции. Такого рода задачи носят название оптимизационных задач. Разработкой общих методов их решения занимаются специальные разделы высшей математики. В силу ограниченности во времени мы рассмотрим некоторые из них: методы линейного программирования и методы дифференциального исчисления.

2 .1.Решение задач на оптимизацию методами линейного программирования

Вопросы для самоконтроля:

1. Что называется моделью?

2. Приведите примеры моделей.

3. Что представляет собой математическая модель?

3. Назовите этапы создания модели.

4. Какую функцию называют целевой?

5. Что значит – оптимизировать функцию?

6. Почему задачи называют задачами линейного программирования?

6. Какую фигуру на плоскости задаёт линейное неравенство?

7. Какую фигуру на плоскости задаёт система линейных неравенств?

8. Какой план называют допустимым? оптимальным?

9. Опишите метод линейного программирования.

Математика – наука о математических моделях.

Математика и экономика – две на первый взгляд далёкие друг от друга науки. Одна -абстрактна, другая –практична. Что здесь может быть общего? Однако, взаимосвязь между этими науками, роль математических методов в анализе экономических процессов были отмечены учёными ещё в ХVIвеке, но только XIX век стал временем серьёзного применения математического аппарата в экономике. Проблемами изучения рынка с помощью математики занимались Антуан Курно (1801-1877), Альфред Маршалл (1842-1924), русские учёные В.К.Дмитриев(1868-1913), Е.Е.Слуцкий(1880-1948), А.А.Чупров (1874-1926) и другие.

XX век можно назвать веком бурного проникновения математических методов в самые различные науки, в том числе и в экономику. В нашей стране создавались центры экономико-математических исследований, в ведущих вузах страны открывались отделения и факультеты по подготовке специалистов в области этих исследований. Имена академиков В.С.Немчинова, А.Г.Агамбегяна и других известны в нашей стране и за рубежом.

Вооружая исследователей – практиков средствами научного поиска, математика сама развивалась. Появились новые разделы математики. Одним из важнейших направлений развития экономической теории стало математическое моделирование экономических процессов. Сегодня математику называют наукой о математических моделях.

Что такое математическая модель?

Определение:

Моделью называется объект, который создаётся для изучения оригинала, отражает его наиболее важные качества и параметры.

Примеры: 1. Фотографию человека можно назвать моделью. Для того, чтобы узнать по внешности человек, нет необходимости знать его рост, вес, социальное положение – от этих характеристик мы отвлекаемся, считая наиболее важными внешние черты.

2. Покупатель купил в магазине три вещи стоимостью 6200, 346, 3600 рублей. Он произвёл вычисления израсходованной суммы: 6200+346+3600 = 4146.

Это числовое равенство – тоже модель - математическая. Здесь представляет интерес только сумма потраченных денег и неважно время покупки, место, погодные условия и т.п.

3. На грампластинке записаны песни в исполнении Ф.И.Шаляпина.

Это тоже модель. Здесь нас прежде всего интересуют голос великого певца, содержание песен. Не представляют интереса , в какой политической обстановке, в каком концертном зале они прозвучали.

4. Всем известна физическая формула S = V*T. Это тоже модель.

Что общего во всех этих примерах?

Общее то, что во всех случаях модель заменяла сам исследуемый объект: какие-то его свойства мы считали более важными, на какие-то не обращали внимания.

Для чего нужна такая замена?

Архитектор создаёт макет застройки жилого района. При обсуждении проекта можно переместить «высотное» здание из одного района в другой, передвинуть будущий парк и т. д. В реальности это было бы невозможно.

Суворов перед штурмом Измаила проводил тренировки своих солдат на специально подготовленных фортификационных сооружениях. Это была модель будущих боевых действий.

Различные экономико-математические модели создаются потому, что проводить эксперименты с экономикой очень сложно или невозможно.

Только космонавты сегодня могут сказать, что видели Землю со стороны, но мы тоже имеем представление о своей планете, т.к. у нас есть её макет-модель - глобус.

В своё время учёные-астрономы, не вставая из-за стола, работая с формулами, «вычислили», открыли две новые планеты - Плутон и Нептун.

Ещё один пример: Люди издавна интересуются , как они сами устроены, как функционирует их организм, но изучать эти вопросы на самом живом человеческом организме очень трудно, ибо до появления особых приборов это было связано с гибелью организма. Тогда ученые стали производить исследования на подобных организмах животных (обезьян, собак, крыс и т.п.). В этих исследованиях животные выступают в качестве моделей человеческого организма.

Процесс построения модели называется моделированием, построение математической модели – математическое моделирование. Можно сказать, что создание математической модели – это перевод с одного языка на другой –с естественного языка, на котором сформулирована проблема, практическая задача, на математический язык.

Модели можно разделить на материальные и идеальные. Примерами материальных моделей служат диски, кассеты, фотографии, макеты и т.п. Идеальные модели часто имеют знаковую форму. Реальные понятия заменяются при этом некоторыми знаками, которые уже легко можно зафиксировать на бумаге в виде текста, графика, таблицы, равенства, неравенства и т.д.

Математическое моделирование относится к классу знакового моделирования. При этом модели могут создаваться из любых математических объектов: чисел, функций, уравнений, графиков и т.д.

Модель может быть более сложной или менее сложной. Какая модель лучше: простая или сложная?

Ответ неоднозначен. Если модель слишком проста, плохо соответствует реальному объекту, не учитывает его каких-то существенных качеств, то даёт результаты, далёкие от действительности. Если же она слишком подробная, учитывает незначительные малейшие детали, то её математическое решение может оказаться слишком трудным, длинным или даже невозможным. Поэтому при выборе модели лучше ориентироваться на «золотую» середину.

Критерием применимости модели служит практика: если модель даёт удовлетворительные результаты, то её используют, если нет, то её корректируют или создают другую.

Моделирование экономических процессов имеет особенности. Какие и почему?

Экономика - одна из сложнейших областей деятельности. Экономические объекты могут описываться сотнями, тысячами параметров, многие носят случайный характер. Кроме того, в экономике действует человеческий фактор. А предсказать поведение человека трудно, подчас невозможно.

Экономика зависит от социального устройства общества, от политики, природных условий и ещё от многих и многих факторов.

И всё - же моделирование экономических явлений, объектов, процессов возможно! Для моделирования экономики применяют не одну модель, а систему моделей. В этой системе есть модели, описывающие разные стороны изучаемого объекта. Есть модели, описывающие экономику страны (их называют макроэкономическими), есть модели экономики отдельного предприятия или даже модель одного экономического события (их называют микроэкономическими). Конечно, процесс создания экономико-математической модели – сложный процесс, требует познаний во многих науках: экономике, математике, социологии, психологии и других. Для того, чтобы хоть немного упростить его, принято выделять в нём несколько наиболее важных этапов:

I. Осмысление задачи, выделение наиболее важных величин, свойств, параметров. Это можно сделать, составляя таблицы, рисуя схемы, графики и т.п.

II .Введение обозначений неизвестных величин.

III. Составление системы ограничений, которым должны удовлетворять введённые величины.

IV. Создание целевой функции и её оптимизация.

Определения:

Целевой функцией называется функция, которая математически выражает цель задачи.

Оптимизировать функцию – это значит найти такие значения переменных, при которых функция принимает минимальное или максимальное (оптимальное) значения.

Задачи линейного программирования

Задачи линейного программирования - один из видов задач математического моделирования. Особенностью их является то, что ограничениями в них являются линейные уравнения и неравенства. Целевая функция также должна быть линейной. Слово программирование здесь используется в смысле планирование – составление планов. Успешно решают такие задачи методом линейного программирования.

В общей теории набор значений переменных (x₁, x₂, ... , x_n ) называется планом задачи. Те планы, которые удовлетворяют системе ограничений, называются допустимыми планами. Оптимальным планом называется тот из допустимых планов, который дает наибольшее (наименьшее) значение целевой функции среди всех ее значений на допустимых планах. Само это наибольшее (наименьшее) значение целевой функции, то есть значение целевой функции на оптимальном плане, называется оптимумом задачи.

Решить задачу производственного планирования - значит найти оптимальный план и оптимум для ее математической модели.

Ответьте на вопросы:

1. Линейное программирование - это:

А.один из приемов разработки программного обеспечения ЭВМ. В.математический метод оптимизации С.определение последовательности действий при проведении общественных мероприятий

2. Какие функции, уравнения и неравенства используются в линейном программировании?

А. только линейные В. любые С. в зависимости от решаемой задачи

3. Методы линейного программирования позволяют определить оптимальное экономическое решение?

А.всегда. В.да, если оно существует С.линейное программирование предназначено для других целей

4. Допустимый план – это:

А.любой план

В. план, удовлетворяющий системе ограничений

С. план, которому соответствует оптимальное значение целевой функции

5. Оптимальный план - это какой план?

А. любой план В. любой допустимый план С. допустимый план, которому соответствует оптимальное значение целевой функции

В качестве примеров задач линейного программирования можно привести следующие часто встречающиеся задачи:

об оптимальном рационе питания

транспортная задача – об оптимальных перевозках

об оптимальном плане.

Графический способ решения задач линейного программирования

Прежде, чем перейти к решению задач линейного программирования по составленной модели, уместно повторить некоторые сведения из школьной программы, касающиеся линейных уравнений и неравенств.

Как известно, графиком линейного уравнения является прямая линия, которую легко построить по двум точкам. Например, если -2х-у+3=0, то, выразив из уравнения у = -2х+3 и составив таблицу значений, получим график – прямую линию.

х х	0	1.5
у	3	0

Обратите внимание! При составлении таблицы значений значения аргумента «х» можно брать любые, но удобнее брать такие, чтобы получить точки пересечения прямой с осями координат (х₁=0, х₂ взять таким, чтобы у = 0).

Если необходимо изобразить то, что задает, например, соотношение 3х+4у ≤ 8, то, заметив, что оно состоит из двух соотношений (уравнения и неравенства), поступают следующим образом:

1) строят график уравнения 3х+4у = 8 – прямую (как мы только что вспомнили), которая делит плоскость на две части - выше этой прямой и ниже её.

2) из этих двух полуплоскостей выбирают ту, которая соответствует знаку неравенства: выше прямой, если знак ≥ или ниже, если знак ≤.

1) строим прямую у = (8 - 3х)/4 (смотри выше).

2) выбираем полуплоскость (заштриховываем), расположенную ниже построенной прямой, т.к. знак неравенства ≤.

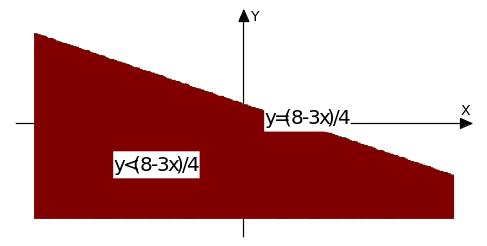
Если необходимо решить систему двух неравенств, то последовательно изображаем полуплоскости, задаваемые всеми неравенствами и выбираем множество, которое является их пересечением.

Например, графическое решение системы имеет вид:

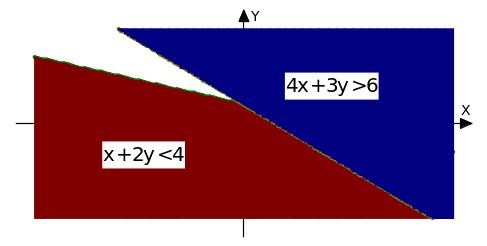
т.е. представляет собой угол, заштрихованный в клеточку.

Изобразите самостоятельно множества, задаваемые следующими соотношениями:

		3. 3х + 2у > 0
	5.	6. x - 2y ≥ 4 7.

Такой графический способ позволит в дальнейшем весьма успешно решать задачи линейного программирования.

Задача №1: (об оптимальном рационе питания)

Чебурашке положено ежедневно съедать не менее 6 единиц белков, 8 единиц жиров и 12 единиц углеводов. Есть два вида продуктов. Одна единица первого продукта содержит 21 единицу белка, 2 единицы жира, 4 единицы углеводов и стоит 3 рубля. Для второго продукта соответствующие цифры следующие:3,2,2 и 2 рубля. Вычислите оптимальный рацион питания Чебурашки, предварительно составив математическую модель для решения задачи.

Решение

Что такое рацион питания в данной ситуации?

- Это два числа, обозначающие количество первого продукта и второго.

Что значит, что рацион должен быть оптимальным?

- Это значит, что Чебурашка должен получить необходимое количество питательных веществ и стоить рацион должен минимально.

Таким образом, у нас 2 неизвестных величины, от которых зависит значение функции – стоимости рациона.

А. Создаю математическую модель

I. этап: осмысление условия задачи.

Очевидно, что все количественные данные можно записать в виде таблицы

	Белки	жиры	углеводы	Цена продукта
Продукт №1	21	2	4	3
Продукт №2	3	2	2	2
всего	Не менее 6	Не менее 8	Не менее 12	минимальна

II. этап: обозначаю неизвестные величины.

Пусть необходимое количество первого продукта будет «х», второго – «у».

III. этап: составляю систему ограничений:

,

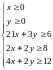Здесь 21х- это количество белка в 1 продукте, 3у- во втором, а 21х+3у- количество белка в

1 и 2 продуктах вместе.

Аналогично составлены следующие суммы.

IV. этап: составляю целевую функцию.

В данном случае она выражает стоимость рациона, т.е. Z(x;y) = 3x + 2y

Математическая модель

Она получается механическим объединением III и IV этапов

Очевидно(?), что это задача линейного программирования.

В. Решение

1. Решаю графическим способом систему ограничений

х х 0 2/7 у1 2 0 х 0 4 у2 4 0 х 0 3 у3 6 0

а) у₁ = 2 - 7х-прямая,

б) у₁≥2-7х – полуплоскость над прямой у₁(почему?)

в) у₂ = 4 - х – прямая,

г) у₂ ≥ 4-х - полуплоскость над прямой у₂

д) у₃ = 6 – 2х – прямая

ж) у₃ ≥ 6 – 2х – полуплоскость над прямой у₃,

В результате:

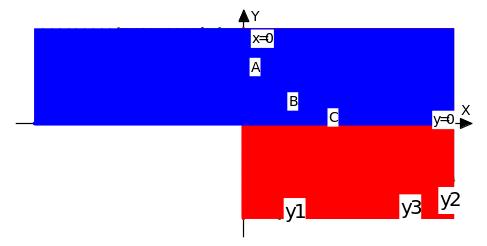
Если внимательно приглядеться, то можно увидеть, что самая «густая» штриховка в множестве, которое можно обозначить, например, уАВСх. Это множество точек и есть графическое решение системы ограничений.

Что означает тот факт, что точка является решением системы ограничений? Как известно, каждая точка плоскости однозначно определяется своими координатами, т.е. парой чисел (х;у). То, что точка является решением системы ограничений значит, что если эти числа подставить в систему ограничений, то каждое неравенство обратиться в верное числовое неравенство, т.е. пара является решением.

Очевидно, что решений найдено бесконечное множество, что нас в данной ситуации не устраивает. Поэтому

2. Выбираю из найденного бесконечного множества решений одно – оптимальное. Как?

Доказано, что своё оптимальное значение целевая функция принимает только в одной из вершин.

В какой? Вопрос этот можно решить по-разному. Мы воспользуемся методом перебора вершин: вычислим стоимость рациона (значения целевой функции) в каждой вершине. Для этого надо знать координаты этих вершин.

Координаты А и С очевидны из построения: А(0;6), С(4;0). Координаты точки В придётся вычислить - как координаты точки пересечения двух прямых: у₂ = у₃:

4 – х = 6 – 2х, х = 2, у = 2,

следовательно, В(2;2).

Z_A(0;6) = 3*2+2*6 = 18,

Z_B(2;2) = 2*2 + 3*2 = 10 - min

Z_C(4;0) = 3*4 + 2*0 = 12

Из этих расчётов видно, что минимальное значение целевая функция (стоимость рациона) принимает в точке В, в которой х = 2 и у = 2. Это означает, что для здоровья Чебурашке всего полезнее съедать ежедневно 2 единицы первого продукта и 2 второго. Это является ответом на заданный в задаче вопрос.

№2: Задача об оптимальных перевозках (транспортная):

Продукцию, производимую на предприятиях «Парнас» и «Самсон» надо развести по фирменным магазинам №1, №2, №3. «Парнас» производит 320 единиц в сутки, «Самсон» - 380. Магазин №1 реализует за сутки 200 единиц, №2 – 280, №3 – 220 единиц. Стоимость перевозки 1 единицы продукции задана таблицей:

магазин предприятие	№1	№2	№3
Парнас	2	4	6
Самсон	4	5	3

Составьте оптимальный план перевозок, т.е. такой, чтобы их стоимость была минимальной.

А. Создадим математическую модель для решения задачи:

2

I. этап: для усвоения условия удобно сделать рисунок:

6

№1 – 200

Парнас: 320

3

4

№3 – 220

Самсон: 380

№2 – 280

План представляет собой 6 чисел: количество продукции, которое нужно перевезти с каждого предприятия в каждый магазин. Значит, неизвестно 6 величин

.

II. этап: Обозначение неизвестных:

Пусть х – количество продукции, перевозимое с предприятия «Парнас» в магазин №1,

у – количество продукции, перевозимое с «Самсона» в магазин №2. Остальные неизвестные можно выразить через х и у, исходя из элементарных соображений, т.е. если магазин №1 принял на реализацию от предприятия «Парнас» х кг продукции, то от предприятия «Самсон» он может принять только недостающие до его объёма реализации килограммы, т.е. 200 – х и т.д.

магазин предприятие	№1	№2	№3
Парнас	х	у	320-х-у
Самсон	200-х	280-у	220-(320-х-у)

III. этап: система ограничений:

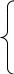
х ≥ 0, у ≥ 0

200 – х ≥ 0

280 – у ≥ 0

х+у-100 ≥ 0

320 – х – у ≥ 0

IV. этап: Составляю целевую функцию.

Здесь она выражает стоимость перевозок – сумма стоимостей перевозок с каждого предприятия в каждый магазин:

Z(x;y) = 2x + 4y + 6(320-x-y) + 4(200-x) + 5(280-y) + 3(x + y – 100) =

=2x+4y+1920-6x+800-4x+1440-5y = 3820-5x-4y.

В результате этих действий получается

Математическая модель:

х ≥ 0, у ≥ 0

200 – х ≥ 0

280 – у ≥ 0

х + у - 100 ≥ 0

320 – х – у ≥ 0

Z(x;y) = 3820 – x – y → min

B. Решение

1. Решаю графически систему ограничений:

Неравенства первой строки говорят о том, что все решение находится в первой четверти.

Остальные неравенства преобразуются к виду:

В результате получается такая картинка:

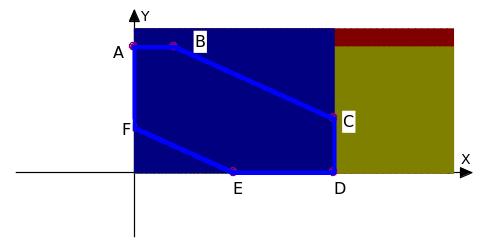
Очевидно, что решение системы ограничений - шестиугольник ABCDEF, т.к. каждая его точка (х;у) удовлетворяет системе. Как видим, решений получено бесконечное множество.

2. В какой точке целевая функция принимает минимальное значение?

Вспоминаем, что своё оптимальное значение целевая функция принимает только в одной из

вершин.

Так же как и в предыдущей задаче вопрос можно решить практическим путём – вычислением стоимости (значения целевой функции) в каждой вершине. Для этого надо знать координаты этих вершин.

А(0;280) – это очевидно.

В: 320-х=280, т.к. В является пересечением прямых, значит, х = 40. В(40;280)

С: у = 320 – 280 = 120, С(200;120)

D(200;0), E(100;0), F(0;120) – очевидно.

Теперь вычисляем значение целевой функции в этих точках:

Z_A(0;280) = 3820-5*0-4*280 = 2700

Z_B(40;280) = 3820-5*40-4*280 =2500

Z_C(200;120) = 3820-5*200-4*120 = 2340 - min

Z_D(200;0) = 3820-5*200-4*0 = 2820

Z_E(100;0) = 3820-5*100-4*0 = 3320

Z_F(0;120) = 3820-5*0-4*120 = 3420

Полученные результаты показывают, что минимальное значение целевой функции (стоимость) достигается в точке С с координатами х = 200, у = 120

Тогда оптимальный план можно записать так:

магазин предприятие	№1	№2	№3
Парнас	200	120	0
Самсон	0	160	220

Это и есть ответ.

№3: Задача о составлении оптимального плана

Составьте оптимальный план производства продукции так, чтобы стоимость

всего произведённого была максимальной, если:

цена 1 единицы каждой продукции 20 денежных единиц, на каждую единицу первой продукции расходуется: 4 единицы сырья,1 ед.материалов, 2 человекодня трудовых ресурсов; второй продукции соответственно- 2,3 и 3.

Общие объёмы ресурсов: трудовых – 12, сырья-16, , материалов-9.

Цена 1 ед.сырья-1 д.е.,материалов-3 д.е.

*Проанализируйте математическую модель этой задачи: как можно увеличить стоимость всей продукции (если можно), если можно привлечь дополнительные ресурсы, а лишние

продать?

Решение

А. Создаю математическую модель:

I. этап: данные задачи удобно в этом случае оформить в виде таблицы:

продукция	Цена продукции	Норма расхода ресурсов
		трудовых	сырьевых	материалов
№1	20	2	4	1
№2	20	3	2	3
всего		12	16	9
Цена ресурсов	-	-	1	3

II. этап: обозначение неизвестных величин.

Т.к. продукции 2 вида, то имеем две неизвестных величины. Пусть количество продукции №1 будет «х», а количество продукции №2 будет «у».

III. этап: составление системы ограничений:

х ≥ 0, Здесь: 2х – это количество трудовых ресурсов, необходимое для

у ≥ 0 производства продукции №1,

4х+2у ≤ 16 3у- это количество трудовых ресурсов, необходимое для

х +3у ≤ 9 производства продукции№2,

2х +3у ≤ 12

2х+3у – количество трудовых ресурсов, необходимое для

производства всей продукции.

Это количество не может превосходить имеющегося в наличии, т.е. 12. Аналогично получаются остальные неравенства.

IV. этап: Создание целевой функции. Здесь она выражает стоимость всей продукции (цену умножаю на количество продукции), поэтому

Z(x;y) = 20x +20y → max

Математическая модель:

х ≥ 0

у ≥ 0

4х+2у ≤ 16

х +3у ≤ 9

2х +3у ≤ 12

Z(x;y) = 20x+20y→max

B. Решение

1. Изображаю полуплоскости, которые задают неравенства системы ограничений (аналогично предыдущей задаче):

у1≤	х	0	4
	у1	8	0
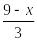
у2 ≤	х	0	9
	у2	3	0
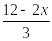
У3≤	х	0	6
	у3	4	0

C

В

А

D

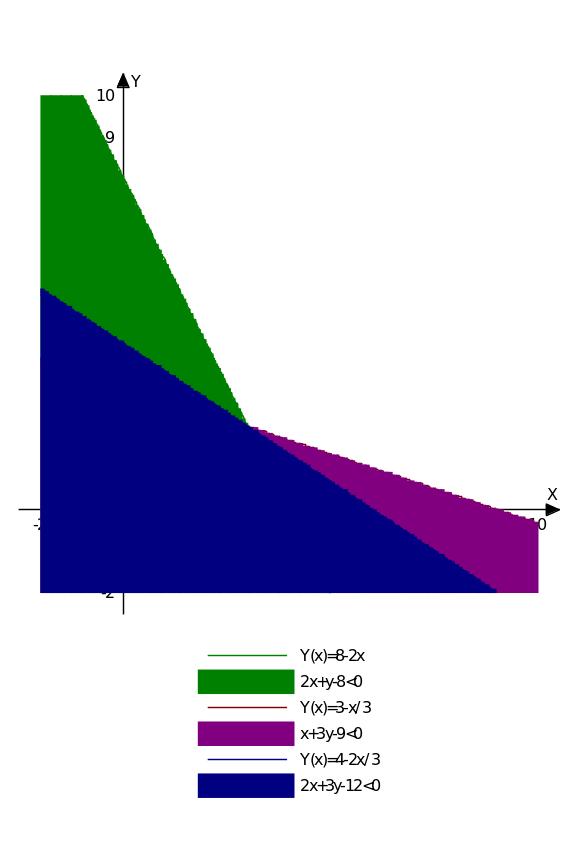
Решением системы ограничений является четырёхугольник ABCD.

2. Koординаты вершин: A(0;3), C(4;0), координаты В надо вычислить (как точки пересечения двух прямых): 9-х=12-2х, х=3, у=2. Значит, В(3;2).

Вычисляю значение целевой функции:

Z_A(0;3) = 20*0 + 20*3 = 60

Z_B(3;2) = 20*3 + 20*2 = 100 - max

Z_C(4;0) = 20*4 + 20*0 = 80

Очевидно, что максимальное значение достигается в точке В(3;2). Поэтому можно записать ответ: оптимальный план представляет собой 3 единицы первой продукции и 2 единицы второй.

*. Если предположить, что в ресурсах мы не ограничены (кроме трудовых), то в этих условиях математическая модель будет выглядеть так:

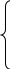
х ≥ 0, у ≥ 0

4х+2у ≥ 0 у₁≥ -2х

х +3у ≥ 0 у₂ ≥ -х/3

2х +3у ≤ 12

Z(x;y) = 20x+20y→max у₃ ≤

1. Решением является треугольник ОАВ:

A

B

O

2. Вычисляю Z_A(0;4) = 80, Z_B(6;0) = 120 - max.

Очевидно, большую стоимость даёт реализация плана (6;0). Вспомним, что реально мы имеем в наличии всё-таки ограниченное количество ресурсов.

Оценим ресурсы по новому плану (6;0):

Сырьё: 4*6 + 2*0 = 24ед., т.к .есть только 16, то 8ед. не хватает.

Материалы: 6 + 3*0 = 6ед., т.к. есть 9ед., то3ед. лишние.

Можно лишние материалы продать: 3*3 = 9ден. ед., на эти деньги можно купить недостающее сырьё: 8*1 = 8ден.ед. Таким образом, получаем 20 + 1 = 21ден.ед. к рассчитанной первоначально сумме.

Как видим, простейший эксперимент на модели даёт возможность перейти к новому плану, дающему увеличение стоимости всего объёма продукции на 20 (120 – 100) денежных ед. за счёт изменения ассортимента при дополнительном вовлечении сырьевых ресурсов и отказа от излишков материалов.

Алгоритм решения задачи линейного программирования

А. Создаю мат. модель:

I этап:…………………………………….

II этап:……………………………………

III этап:…………………………………..

IV этап:…………………………………..

Математическая модель:

В. Решаю задачу:

1. Решаю графически систему ограничений. Для этого изображаю полуплоскости, задаваемые неравенствами модели:

у₁ ………-это полуплоскость выше (ниже) прямой у. (Выше или ниже – это зависит от

у₂ ……… знака: больше или меньше)

…………

у_п …………

Вывод:

решением системы ограничений является пересечение построенных полуплоскостей.

Таких решений бесконечно много.

Нужно выбрать одно – оптимальное, исходя из того, что своё оптимальное значение целевая функция принимает только в одной из вершин.

2.Выбираю, вычисляя значения целевой функции в вершинах. Координаты вершин вычисляются как координаты точек пересечения соответствующих прямых, например, В:у₂ = у₅ .

Z_А = ……., Z_В = …….

………………………

Z_М = …………………. – очевидно – оптимально.

3.Записать ответ, перейдя с языка математики на естественный язык.

Построение математической модели приносит очевидную пользу:

Построение модели позволяет превратить содержательную экономическую задачу (в нашем примере - задачу о составлении производственного плана) в чисто математическую задачу о поиске максимального значения функции при условии, что переменные подчинены определенной системе ограничений. При решении этой математической задачи можно не знать ничего о смысле входящих в нее переменных и выражений, забыть, что речь идет о продуктах питания, ресурсах и выручке. Это позволяет использовать при ее решении универсальные математические методы, привлечь для решения вычислительную технику и программные средства.