2. Расчет на усталостный изгиб зубьев

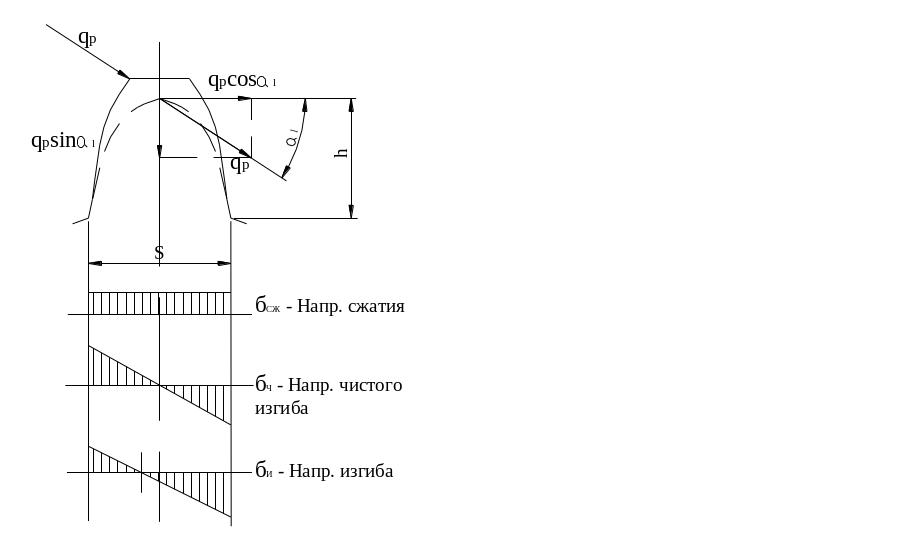
Опасным нагружением считается такое, которое соответствует моменту начала входа зуба в зацепление. Интенсивность нагрузки q_p создает две составляющие, из которых одна сжимает, а другая нагибает зуб.

Опасным сечением считается сечение у корня зуба со стороны растянутых волокон, так как закаленные стальные зубья слабее сопротивляются растяжению, чем сжатию.

a_l - угол зацепления при вершине зуба.

b = 1.

Входящие в эти формулы величины S, h и a_l аналитически трудно определимы, поэтому формула преобразуется так, чтобы в скобках были безразмерные величины, совокупность которых определяется по таблицам или графикам:

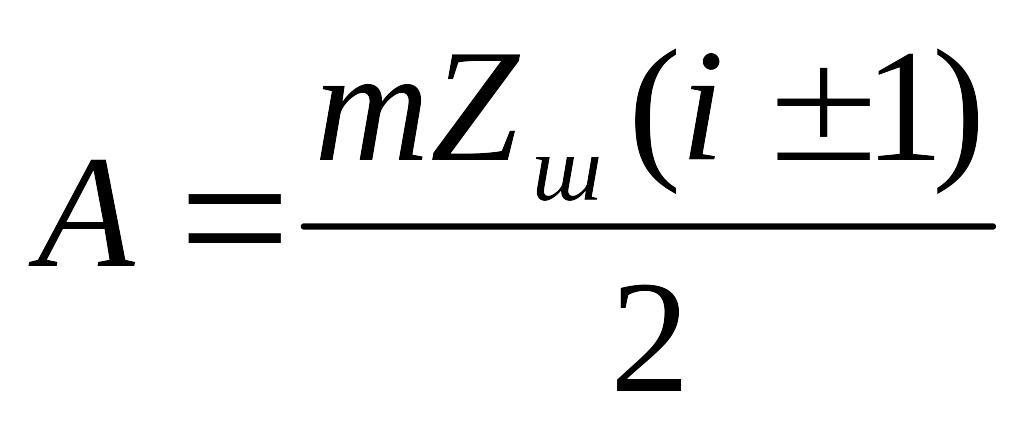
Здесь: y - коэффициент формы зуба; определяется по таблицам или графикам в зависимости от числа зубьев и коэффициента коррекции (если она есть).

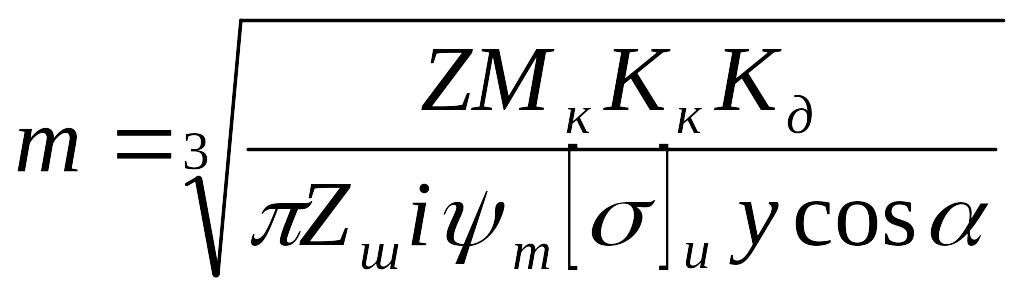
Подставив значение q, введенное ранее, получаем проверочную формулу:

Для проектных расчетов формула преобразуется с введением коэффициента относительной модульной ширины шестерни:

обычно y_м = 6 –10

Выражая величины А и b через модуль, получаем проектную формулу:

Обычно шестерни закрытых передач рассчитываются на контактную прочность (опасным является питинг) и проверяются на изгиб; шестерни открытых передач, для которых питинг не опасен, рассчитываются только на изгиб.

Определение допускаемых напряжений изгиба

Допускаемые напряжения определяются как часть от предела усталости (выносливости) материала при симметричном цикле нагружения:

- для нереверсивных передач;

- для реверсивных передач.

Здесь: n₁ - коэффициент запаса прочности по пределу усталости, К_s - коэффициент концентрации напряжений у ножки зуба, K_рн - коэффициент режима нагрузки по изгибу, можно принимать его равным 1 для большинства передач (только для очень тихоходных передач он может быть больше единицы).

Особенности расчета косозубых цилиндрических шестерен

Рис.2

Принципиально расчетные формулы для косозубых шестерен те же, что и для прямозубых, отличие заключается в следующем:

Таблица 2

Оценочный параметр	Прямозубые	Косозубые
Нагрузка на зуб
Длина контактных линий
Эпюра распределения нагрузки на зуб	Равномерная	Неравномерная
	(рис. 1а)	- в середине зуба (рис.1б)

Неравномерность эпюры является положительным фактором, спасая зубья от кромочных давлений при небольшом перекосе ее в зацеплении; она является следствием неравной жесткости головки и ножки зуба.

Особенности расчета конических прямозубых шестерен

Конические шестерни рассчитываются как эквивалентные им цилиндрические.

Окружное усилие определяется по среднему диаметру, расчетным является средний модуль. При определении коэффициента формы зуба принимается эквивалентное число зубьев.

Коррекция зубьев шестерен

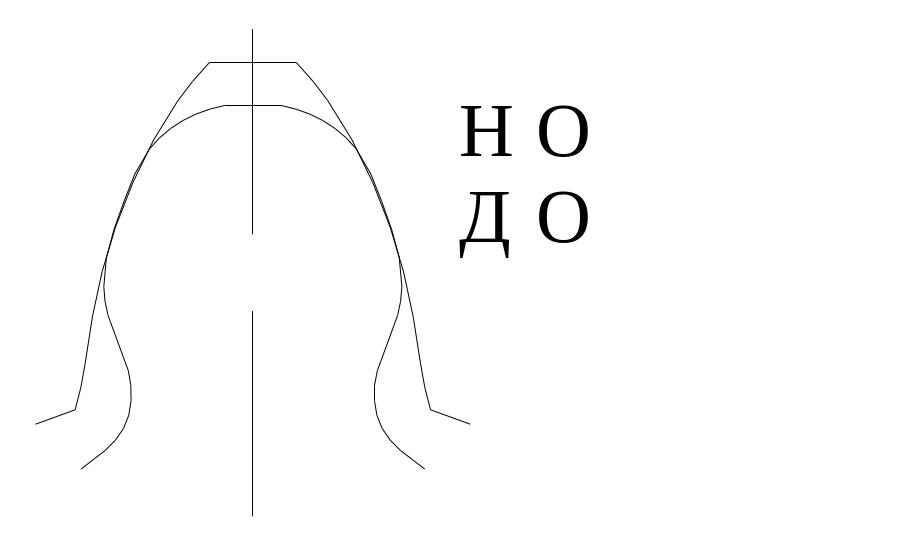
В целях уменьшения габаритов и веса машин желательно у малых шестерен число зубьев делать минимальным, однако этому препятствует подрез ножки зуба, который для эвольвентного двадцатиградусного зацепления имеет место при Z < 17 зубьев. Вводя коррекцию (теоретическое исправление профиля), можно уменьшить Z_min до 14 зубьев и даже менее.

1. Угловая коррекция (фау-коррекция) заключается в смещении профиля зубьев малой шестерни в плюс (от центра) на величину:

V = xm

где x - коэффициент коррекции.

При этом увеличивается на величину V межцентровое расстояние, а также угол зацепления, так как при раздвижке центров раздвигаются соответственно и основные окружности, к которым касательна линия зацепления.

2. Высотная коррекция (фау-нуль-коррекция), при которой профиль зубьев малой шестерни смещается в плюс (+V), а профиль зубьев колеса на столько же - в минус (-V). При этом межцентровое расстояние и угол зацепление не меняются, изменяются лишь относительная высота головки и ножки зубьев.

Изготовление корригированных шестерен не представляет никаких трудностей.

КПД зубчатых передач

Для закрытых передач в среднем:

цилиндрических h =0,98,

конических h = 0,97.

Для открытых передач:

цилиндрических h = 0,97,

конических h = 0,96 .

Эти цифры включают также потери в опорах качения, которые невелики и составляют от 0,25 до 0,5 % на опору при надежной смазке.

Планетарные зубчатые передачи

Планетарными называют передачи, имеющие зубчатые колёса с перемещающимися осями. Эти подвижные колёса подобно планетам Солнечной системы вращаются вокруг своих осей и одновременно перемещаются вместе с осями, совершая плоское движение, называются они сателлитами (лат. satellitum – спутник). Подвижные колёса катятся по центральным колёсам (их иногда называют солнечными колёсами), имея с ними внешнее, а с корончатым колесом внутреннее зацепление. Оси сателлитов закреплены в водиле и вращаются вместе с ним вокруг центральной оси.

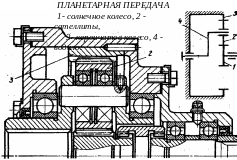
Планетарные передачи имеют ряд преимуществ перед обычными:

• большие передаточные отношения при малых габаритах и массе;

• возможность сложения или разложения механической мощности;

• лёгкое управление и регулирование скорости;

• малый шум вследствие замыкания сил в механизме.

В планетарных передачах широко применяют внутреннее зубчатое зацепление с углом a_w = 30^о.

Для обеспечения сборки планетарных передач необходимо соблюдать условие соосности (совпадение геометрических центров колёс); условие сборки (сумма зубьев центральных колёс кратна числу сателлитов) и соседства (вершины зубьев сателлитов не соприкасаются друг с другом).

Зубчатые колёса планетарных передач рассчитываются по тем же законам, что и колёса обычных цилиндрических передач.