2) По заполненным клеткам;

3) по незаполненным клеткам.

Вопрос 13

Транспортная задача называется задачей с правильным балансом, а её модель закрытой если:

1) число Поставщиков равно числу Потребителей;

2) число Поставщиков больше числа Потребителей;

3)Суммарные запасы Поставщиков равны суммарным запросам Потребителей.

Вопрос 14

Определите количество решений для задачи линейного программирования

,

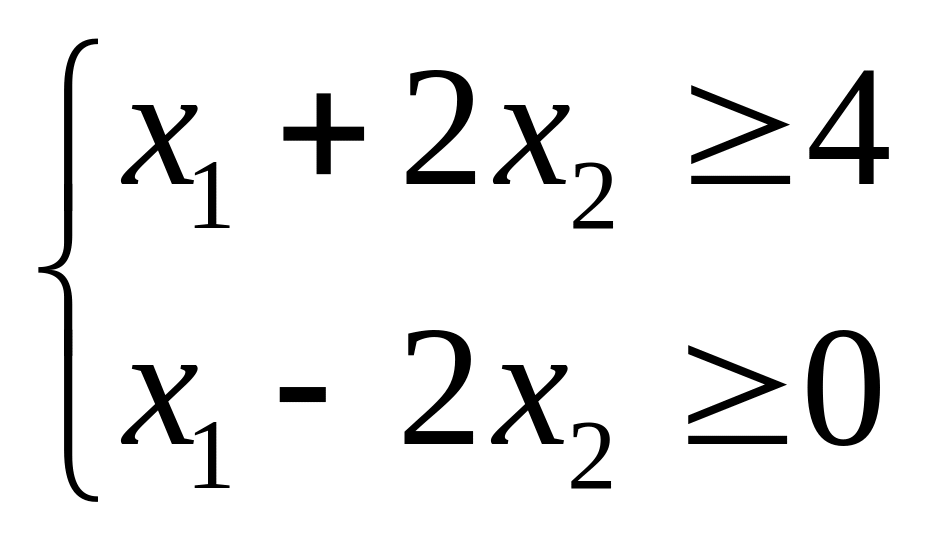
1)	одно оптимальное решение;
2)	два оптимальных решения;
3)	бесконечное множество оптимальных решений;
4)	нет оптимального решения.

1)

2

3)

4)

Литература

1. Афонина Т.Н. Приложение элементов линейной алгебры к задачам экономики и управления: Учеб.-метод. пособие по курсу «математика» для спец. 061100. – Орел: Изд-во ОРАГС, 2001.

2. Вентцель Е.С. Исследование операций. М.: Сов.радио, 1972.

3. Высшая математика для экономистов/ Под ред. Н.Ш. Кремера. 3-е изд. М.: Высшее образование, 2008.

4. Высшая математика для экономистов. Учеб. пособие для вузов / Серия «Высшее образование». Ростов н/Д: Феникс, 2004.

5. .Грес П.В. Математика для гуманитариев: Учебник для вузов: Рек. Мин. обр. – М.: Логос, 2003.

6. Исследование операций в экономике: Учебное пособие/ Н.Ш.Кремер, Б.А.Путко, И.М.Тришин, М.Н.Фридман/ Под ред. Н.Ш. Кремера . 2-е изд. - М.: Юрайт, 2010.

7. Таха Х. Введение в исследование операций. М.: Мир, 1985.

Глоссарий

Двойственная задача - это вспомогательная задача ЛП, получаемая с помощью определенных правил непосредственно из условий исходной задачи.

Задача линейного программирования (ЛП) записана в канонической форме, если её целевая функция максимизируется, ограничения имеют вид равенств с неотрицательной правой частью, и все переменные неотрицательны.

Задача ЛП в канонической форме имеет вид

Задача об использовании ресурсов (задача планирования производства).

Предприятие выпускает n видов продукции с использованием m видов ограниченных ресурсов.

Известны:

b_i (i=1,2,…m) – запас i-го вида,

a_ij (i=1,2,…m, j=1,2,…n) – количество ресурса i-го вида, идущего на изготовление единицы продукции j-го вида,

C_j (j=1,2,…n) - доход от реализации единицы продукции j-го вида.

Составить такой план выпуска продукции, чтобы при ее реализации получить максимальный доход.

Задача составления рациона (задача о смесях).

Имеется n видов кормов,

В каждой порции смеси содержится m питательных веществ в количествах не менее b_i (i=1,2,…m),

Известно: a_ij (i=1,2,…m, j=1,2,…n) – количество i-го питательного вещества, содержащееся в единице корма j-го вида,

с_j (j=1,2,…n) – стоимость единицы корма j-го вида.

Требуется: смешать имеющиеся корма так, чтобы обеспечить заданную питательность при минимальных затратах на корма.

Линии уровня. Рассмотрим целевую функцию f(x)=c₁x₁+c₂x₂. Линии уровня c₁x₁+c₂x₂=α (α R) образуют семейство параллельных прямых. Вектор является вектором нормали к этим прямым и показывает направление возрастания целевой функции. Вектор будет показывать направление убывания целевой функции.

Матричная форма записи задачи линейного программирования.

Задача об использовании ресурсов имеет вид:

Задача о смесях имеет вид

Метод северо-западного угла.

Согласно этому методу запасы очередного Поставщика используются для обеспечения запросов очередных Потребителей до тех пор, пока не будут исчерпаны полностью. После чего используются запасы следующего по номеру Поставщика.

Заполнение таблицы транспортной задачи начинается с левого верхнего угла и состоит из ряда однотипных шагов. На каждом шаге, исходя из запасов очередного Поставщика и запросов очередного Потребителя, заполняется только одна клетка и соответственно исключается из рассмотрения один Поставщик или Потребитель.

Опорной прямой называется линия уровня, которая имеет хотя бы одну общую точку с областью допустимых решений и по отношению к которой эта область находится в одной из полуплоскостей.

Опорным решением задачи ЛП называется такое допустимое решение , для которого векторы условий (столбцы коэффициентов при неизвестных в системе ограничений) А₁, А₂, :::А_m, соответствующие положительным координатам, линейно независимы.

Переменная является базисной, если она входит только в одно из уравнений с коэффициентом, равным 1. Все остальные переменные являются небазисными. Частное решение, полученное приравниванием небазисных переменных нулю и нахождение значений базисных переменных, называется базисным решением.

Теорема. Целевая функция задачи ЛП достигает своего экстремального значения в угловой точке многогранника решений.

Теоремы двойственности позволяют установить взаимосвязь межу оптимальными решениями пары двойственных задач. Решив одну из пары двойственных задач, можно или найти оптимальное решение другой задачи, не решая ее, или установить его отсутствие.

Транспортная задача. Пусть имеется m поставщиков А₁, А₂, …А_m однородного груза в количества а1, а2, а m единиц и n потребителей B_1, В₂, …В_n этого груза, потребность которых составляет соответственно b₁,b₂, b_n единиц.

Известны стоимости перевозок единицы груза от i-го поставщика к j-му потребителю

с_ij (i=1, 2,…m, j=1,2,…n).

Требуется составить такой план перевозок, который обеспечит минимальные транспортные расходы.

Учебное-издание

к.т.н., доц. Гусакова Валентина Ивановна

к.э.н., преп. Кривошлыков Виктор Николаевич

к.э.н., доц. Шепелова Наталья Сергеевна