Задачи для самостоятельной работы Разделы: «Геометрический метод решения задач линейного программирования» и «Симплексный метод»

Решить задачи линейного программирования графическим методом и симплексным методом

1. 

2. 

3. 

4. 

5. 

6. 

7. 

8. 

9. 

10. 

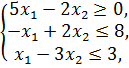
Раздел «Двойственные задачи»

Составить задачу, двойственную к данной.

1.

2.

3.

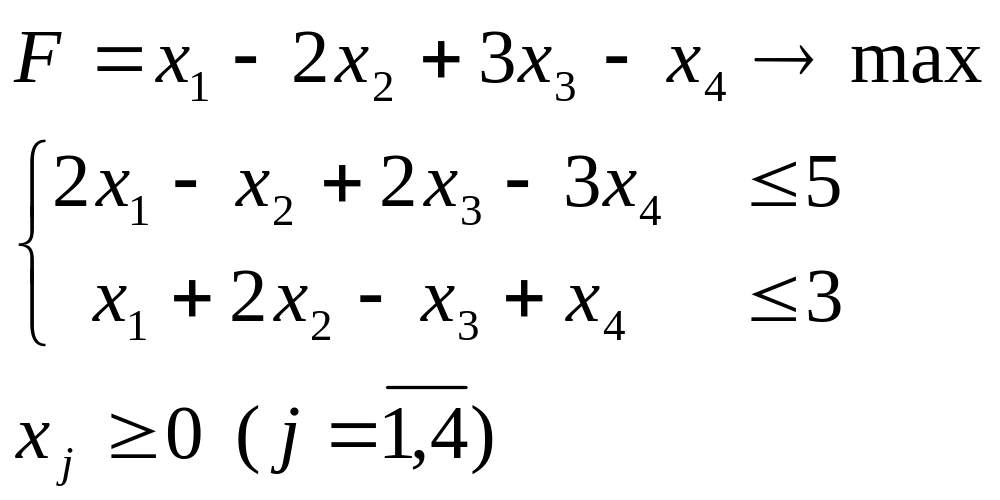
4.

5.

6.

7.

8.

9.

10.

Раздел «Транспортная задача»

Решить транспортную задачу методом потенциалов.

Cij	B1	B2	B3	B4
A1	6	4	3	7	40
A2	2	7	5	9	50
A3	10	12	6	8	80
	20	50	40	60

2. Cij	B1	B2	B3	B4
   A1	6	4	3	8	70
   A2	7	4	1	4	90
   A3	2	4	6	3	100
   	80	90	50	40

3. Cij	B1	B2	B3	B4
   A1	7	5	3	4	90
   A2	6	4	2	5	110
   A3	1	6	5	4	120
   	100	110	60	50

4. Cij	B1	B2	B3	B4
   A1	5	3	5	8	30
   A2	1	5	4	2	40
   A3	3	9	5	3	20
   	10	30	20	30

Cij	B1	B2	B3	B4
A1	6	4	3	7	40
A2	2	7	4	8	60
A3	9	10	5	7	50
	30	40	40	40

6. Cij	B1	B2	B3	B4
   A1	8	5	3	5	60
   A2	2	7	5	9	60
   A3	1	3	5	2	80
   	70	40	50	40

7. Cij	B1	B2	B3	B4
   A1	8	6	4	5	80
   A2	7	5	3	6	60
   A3	2	7	6	5	40
   	50	50	35	45

8. Cij	B1	B2	B3	B4
   A1	6	4	2	3	75
   A2	5	3	1	4	75
   A3	2	6	5	4	50
   	40	60	60	40

Cij	B1	B2	B3	B4
A1	4	2	1	5	70
A2	2	7	5	9	50
A3	8	9	3	5	90
	60	80	40	30

Cij	B1	B2	B3	B4
A1	5	3	2	6	40
A2	1	6	4	8	80
A3	7	9	3	6	70
	30	50	60	50

Тесты

Вопрос 1

Привести задачу линейного программирования к канонической форме

.

1

1)
2)
3)
4)

Вопрос 2

Целевая функция имеет вид: , тогда вектор нормали к линиям уровня равен:

1) (2, 1);

2) (2, -3);

3)(-3,2);

4)(1,-3).

Вопрос 3

В каком виде должна быть записана модель задачи линейного программирования для решения ее симплекс методом?

1)в каноническом виде;

2) в виде квадратной матрицы;

3) в виде диагональной матрицы;

4) в виде расширенной матрицы.

Вопрос 4

Целевая функция задачи линейного программирования достигает своего единственного экстремального значения:

1) внутри многогранника решений;

2) в угловой точке многогранника решений;

3)всегда на линии, соединяющей две соседние угловые точки многогранника решений.

Вопрос 5

Как изменяется значения целевой функции на линиях уровня при перемещении в направлении их нормали:

1) возрастает;

2) убывает;

3) остается неизменным.

Вопрос 6

Если целевая функция задачи линейного программирования достигает экстремум в двух угловых точках, то задача

1) имеет два решения;

2) имеет бесконечное множество решений;

3) правильный ответ не указан.

Вопрос 7

При решении задачи линейного программирования симплексным методом для выбора переменной, вводимой в базис (для выбора ведущего столбца):

1) выбирается переменная, имеющая максимальный коэффициент среди положительных коэффициентов в строке для целевой функции;

2) выбирается переменная, имеющая минимальный коэффициент среди положительных коэффициентов в строке для целевой функции;