
Контроль отлаженности ПО в процессе отладки. Гипотеза Джелинского – Моранды и математическая модель надежности ПО
Лабораторные работы №5-6
Версия 4
Цель работы : Определение параметров модели надежности ПО. Прогнозирование надежности ПО при отладке и эксплуатации.
В результате выполнения данных лабораторных работ студент получает навык:
1) определения момента достижения ПО требуемой надежности в процессе отладки,
2) использования метода наименьших квадратов для обработки данных,
Теоретические основы.
Крайне желательно иметь модель прогнозирования надежности ПО, по которой можно было оценивать, например, необходимость продолжения отладки, планировать точку останова этого процесса.
На пути создания такой достаточно общей и универсальной модели казалось бы имеются два препятствия:
ПО чрезвычайно разнообразно по назначению и сложности,
ПО разрабатывается различными людьми, частота ошибок у них отличается во много раз.
Однако, эти препятствия преодолеваются, если допустить наличие в модели надежности свободных параметров, которые для конкретного ПО, разработанного конкретными людьми, могут быть определены по наблюдениям за проявлением ошибок в этом ПО на определенном интервале времени.
При этом число свободных параметров модели желательно иметь небольшим, а число экспериментальных данных наоборот большим. При этом опасаться того, что число переменных может стать меньше числа уравнений для их определения, не надо.
Метод наименьших квадратов (МНК), которым мы будем пользоваться, не только фильтрует случайные ошибки экспериментальных данных, но и позволяет получать решение переопределенной в алгебраическом смысле системы уравнений.
Модель Джелинского – Моранды
Ошибки в ПО имеют скрытый характер и проявляются только при определенных наборах входных данных. Те грубые ошибки в ПО, которые проявляются сразу при любых исходных данных, сразу же и устраняются. Математическая модель проявления ошибок в ПО Джелинского – Моранды имеет понятный физический смысл: чем больше ошибок в ПО, тем чаще они проявляются при работе. По мере возрастания отлаженности ПО, уменьшается количество оставшихся в нем ошибок и частота их проявления также падает.
Математическая формулировка гипотезы Джелинского – Моранды:
интенсивность (скорость) проявления ошибок в ПО пропорциональна числу оставшихся ошибок.
dn/dt =K×(N0 – n)
или обозначая среднюю интенсивность проявления ошибок
=
К
![]() (No-n).
(No-n).
Здесь N0 – начальное число ошибок ,
n –число обнаруженных ошибок,
К – коэффициент пропорциональности
Рассмотренная модель изменения надежности ПО Джелинского - Моранды позволяет, основываясь на наблюдениях за процессом проявления ошибок в ПО, определить характеристику надежности ПО – интенсивность проявления ошибок , а точнее начальное количество ошибок N0 и параметр К , определяющий скорость проявления ошибок.
Конечно же никакая модель не может предсказать конкретное место ошибки, но это и не надо для поставленных целей.
Решение упомянутого выше дифференциального уравнения первого порядка относительно числа проявившихся ошибок n
n = N0 ( 1 – е-кt ) и
![]() N0
е-кt
К>0
N0
е-кt
К>0
Можно доказать, что данные выражения
справедливы для математических ожиданий
![]() ,n,Nо,
если рассматривать процесс проявления
ошибок в ПО, как случайный, так как
наблюдаемый процесс проявления ошибок
в ПО имеет случайный характер и связан
с сочетанием ряда случайных факторов.
Например, в зависимости от случайного
набора входных данных ошибки в ПО,
количество которых также случайно,
могут проявляться, а могут и не проявляться.
,n,Nо,
если рассматривать процесс проявления
ошибок в ПО, как случайный, так как
наблюдаемый процесс проявления ошибок
в ПО имеет случайный характер и связан
с сочетанием ряда случайных факторов.
Например, в зависимости от случайного
набора входных данных ошибки в ПО,
количество которых также случайно,
могут проявляться, а могут и не проявляться.
При экспериментальных наблюдениях за проявлением ошибок в ПО удобнее не рассматривать общее количество проявившихся ошибок с нарастающим итогом, а рассматривать количество ошибок, проявившихся на фиксированных интервалах времени. Запишем выражение для количества ошибок, проявившихся на интервале ti, полагая равномерным шаг наблюдений за проявлениями ошибок t.
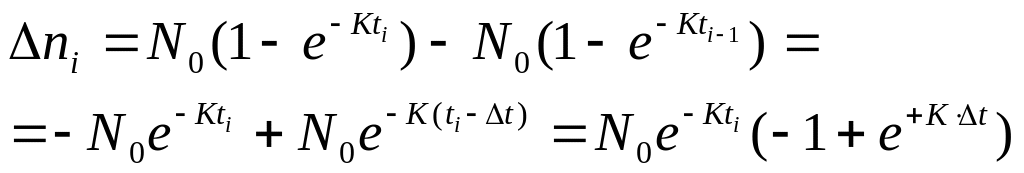 Здесь
ni
- приращение количества обнаруженных
ошибок на интервале t.
Здесь
ni
- приращение количества обнаруженных
ошибок на интервале t.
Пусть шаг t можно выбрать так, чтобы произведение Кt 1.
Тогда, разлагая exp функцию в ряд и пренебрегая членами выше 1-ой степени Кt, как малыми, имеем :
еxp(x)=1+х/1!+х^2/2!+…..
![]()
В данном уравнении два неизвестных N0 и К. Для их определения достаточно рассмотреть два различных интервала t - будет два уравнения с двумя неизвестными.
Однако, возникает вопрос какую пару интервалов из r >2 имеющихся интервалов наблюдений выбрать для определения N0 и К, так как каждой паре интервалов соответствует в общем случае свое решение относительно N0 и К.
Полученное по каждой паре случайно «пляшущих» данных решение не соответствует всей совокупности экспериментальных данных и в этом смысле неверно. Таким образом, подход, связанный с выбором 2 наблюдений, приводит к неправильному результату. Нужно использовать всю совокупность наблюдений. Однако, это на первый взгляд приведет к получению переопределенной системы уравнений (число уравнений, больше числа неизвестных).
