Многовариантная задача

Составить электрохимическую цепь из предложенных электродов и рассмотреть для стандартных условий его работу:

а) указать анод, катод и определить знаки электродов;

б) написать уравнения электродных процессов;

в) определить направление движения электронов во внешней цепи;

г) рассчитать ЭДС элемента;

д) рассчитать термодинамические характеристики реакции, протекающей в гальваническом элементе.

Вариант	Электроды
1	Mn2+ (a = 0,001) / Mn; Fe3+ (a = 1), Pt / Fe2+ (a = 0,2)
2	Cr3+ (a = 0,5) / Cr; Pt, O2 / OHˉ (a = 0,1)
3	Mg2+ (a = 0,1) / Mg; Pt, Cl2 / 2Clˉ (a = 0,01)
4	Cu+ (a = 0,1) / Cu; Pt, F2 / 2Fˉ (a = 0,2)
5	Pb2+ (a = 0,1) / Pb; 2H+ (a = 0,01) / H2, Pt
6	Zn2+ (a = 0,02) / Zn; Cr2O72ˉ (a = 0,01), H+ (a = 0,1), Pt / Cr3+ (a = 0,01)
7	Fe2+ (a = 1) / Fe; Ag+ (a = 0,02) / Ag
8	S / S2ˉ (a = 0,01); Pt, F2 / 2Fˉ (a = 0,2)
9	Cd2+ (a = 0,001) / Cd; Pt, Cl2 / 2Clˉ (a = 0,01)
10	Se / Se2ˉ (a = 0,001); Mg2+ (a = 0,1) / Mg
11	Cr3+ (a = 0,02) / Cr; Cu+ (a = 0,01) / Cu
12	Ag+ (a = 0,001) / Ag; Pt, F2 / 2Fˉ (a = 0,02)
13	Cr2O72ˉ (a = 0,01), H+ (a = 0,1), Pt / Cr3+ (a = 0,01); Pt, O2 / OHˉ (a = 0,1)
14	Mn2+ (a = 0,001) / Mn; Pt, Cl2 / 2Clˉ (a = 0,001)
15	Tl2+ (a = 0,03) / Tl; Fe3+ (a = 0,01), Pt / Fe2+ (a = 0,2)

V. Поверхностные явления Теоретические основы раздела

Известно, что любая поверхность обладает свободной поверхностной энергией G, величина которой определяется как произведение поверхностного натяжения σ на величину площади поверхности S:

G = σ S. (5.1)

Самопроизвольное изменение концентрации вещества на поверхности раздела фаз по сравнению с его концентрацией внутри фазы называют адсорбцией.

Количественно процесс мономолекулярной адсорбции на поверхности раствора может быть выражен уравнением Гиббса:

, (5.2)

где Г – величина адсорбции, моль/м²;

с – концентрация вещества адсорбтива в растворе, моль/м³;

- поверхностная активность, характеризующая изменение σ в зависимости от концентрации при S = const;

Т – температура системы, К;

R – универсальная газовая постоянная. Дж/моль К.

На границе фаз «жидкость – твердое тело» или «газ – твердое вещество» применяют уравнение Лэнгмюра:

или , (5.3)

где Г – удельная адсорбция;

Г_∞ - предельная максимальная адсорбция;

С – концентрация адсорбтива;

Р – давление адсорбтива;

К – постоянная величина.

Уравнение Лэнгмюра может быть представлено в виде:

(5.4)

или

(5.5)

или

, (5.6)

где V – объем адсорбированного газа;

Vm – объем адсорбированного газа, полностью покрывающего поверхность 1 г адсорбента (объемы V и Vm приведены к нормальным условиям).

Графическое изображение уравнения приведено на рисунке:

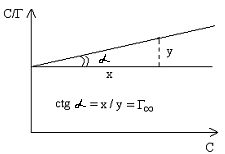
При известной величине Г_∞ может быть вычислена площадь, занимаемая одной молекулой адсорбтива в состоянии насыщения:

, м²/молекула (5.7)

Толщина адсорбированного слоя δ вычисляется по уравнению:

, (5.8)

где М – молярная масса адсорбтива, г/моль;

d – плотность адсорбтива;

N₀ – число Авогадро.

Площадь поверхности S 1 г адсорбтива равна:

, (5.9)

где S - площадь одной молекулы адсорбтива на поверхности адсорбента.

При адсорбции на поверхности многих адсорбентов образуется полимолекулярный адсорбционный слой. Полимолекулярная адсорбция описывается теорией БЭТ, которая устанавливает зависимость между адсорбционной емкостью насыщенного монослоя а_m, удельной адсорбцией а, равновесным давлением газа Р и величиной k – константой, зависящей от энергии взаимодействия молекул в адсорбционном слое.

Уравнение БЭТ в виде уравнения прямой линии имеет вид:

, (5.10)

где P_S – давление насыщенного пара.

Для определения удельной поверхности адсорбента S строят график зависимости: 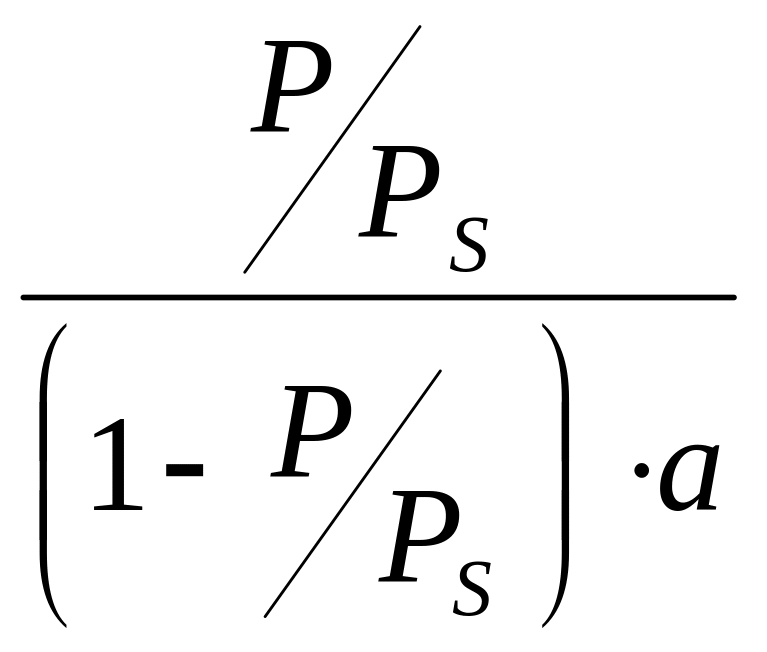от .

По угловому коэффициенту прямой, равному (k – 1)(ka_m)^-1, и величине отрезка, отсекаемого на оси ординат при = 0, равного (ka_m)^-1 рассчитывается a_m. Удельная поверхность S вычисляется по формуле:

S = S₀ ∙ a_m ∙ N₀, (5.11)

где S₀ – площадь, занимаемая одной молекулой газа в адсорбционном слое;

N₀ – постоянная Авогадро.

На практике для вычисления величины адсорбции получило распространение также эмпирическое уравнение Фрейндлиха:

, (5.12)

где Х – количество адсорбированного вещества, моль;

m – масса адсорбента, г;

С – равновесная концентрация;

К и n – эмпирические константы.

В логарифмическом виде уравнение Фрейндлиха представляет уравнение прямой:

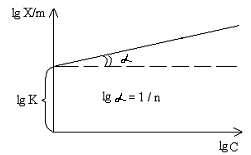
При графическом построении в осях координат «lg X/m – lg C» отрезок, отсекаемый прямой на оси ординат, дает значение lg K, а тангенс угла дает значение 1 / n, т.к. последний составляет угловой коэффициент в уравнении 5.13:

. (5.13)

Ионно-обменная адсорбция

На границе раздела водного раствора и твердого адсорбента практически всегда возникает двойной электрический слой, обусловленный диссоциацией на ионы как растворенных, так и адсорбированных веществ. Кроме того, у ряда адсорбентов существует способность избирательно адсорбировать из раствора ионы одного какого-либо вида.

Адсорбированные ионы на поверхности, находясь в динамическом равновесии с ионами раствора, обмениваются в строго эквивалентном количестве на ионы того же знака, присутствующие в растворе. Такую адсорбцию называют ионно-обменной адсорбцией.

Количественное соотношение между концентрациями обменивающихся ионов устанавливается уравнением Никольского:

, (5.14)

где а₁ и а₂ – активности ионов в равновесном растворе;

х₁ и х₂ – равновесное количество ионов в твердой фазе;

z₁ и z₂ – заряды обменивающихся ионов;

К – константа ионного обмена.

Типовые расчеты

Пример 1

При адсорбции аргона коксовым углем при 194,7 К получены следующие результаты:

Р1, Па	31,9∙103	130,5∙103	290,0∙103
Р1, мм.рт.ст.	24,0	98,4	218,0
Г1, мг/г	5,0	15,4	24,0

Рассчитайте постоянные в уравнении Лэнгмюра.

Решение.

Согласно уравнению Лэнгмюра Г/Г_∞ является угловым коэффициентом зависимости между Р/Г и Р, а lg 1/КГ_∞ - отрезком, отсекаемым этой прямой на оси ординат.

Вычисляем величины Р/Г:

Р, Па	31,9∙103	130,5∙103	290,0∙103
Р/Г	6,4∙103	8,7∙103	12,1∙103

По полученным данным строим график, отложив по оси абсцисс Р, а по оси ординат – Р/Г:

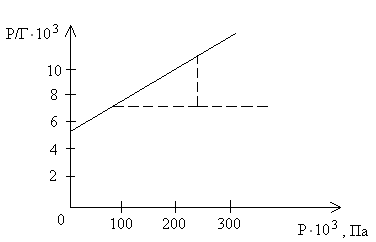
Как видно из графика:

1/Г_∞ = (11 - 7) / (240 – 60) = 0,0222

Отсюда Г_∞ = 45, 1/КГ_∞ = 5,7∙10³, тогда

К = 1 / 5,37 ∙ 45 = 0,004.

Пример 2

При исследовании поверхностной активности растворов уксусной кислоты при 20⁰С были получены следующие результаты:

Концентрация кислоты, моль/л	0,00	0,01	0,10	0,50	1,00
Поверхностное натяжение, дин/см	73,26	70,02	66,88	61,66	57,28

Найти величины Г, δ и площади, занимаемой одной молекулой уксусной кислоты при разных концентрациях.

Решение.

Воспользуемся уравнением Гиббса . Находим средние значения Сср, ∆С, ∆σ и ∆σ/∆С (см. таблицу).

Сср	∆С	∆σ	∆σ/∆С
С1 = =0,005	0,01-0,00=0,01	70,02-73,26= -3,24	-3,24/0,01= -324
С2 = =0,055	0,1-0,01=0,09	66,88-70,02= -3,14	-3,14/0,09= -34,9
С3 = =0,300	0,5-0,1=0,04	61,16-66,88= -5,22	-5,22-0,4= -13,05
С4 = =0,750	1,0-0,5=0,5	57,28-61,66= -4,38	-4,38/0,5= -8,76

По уравнению Гиббса вычисляем величину адсорбции:

Г₁ = моль/см²,

Г₂ = 0,8 ∙ 10^-10 моль/см²,

Г₃ = 1,65 ∙ 10^-10 моль/см²,

Г₄ = 2,75 ∙ 10^-10 моль/см².

Площади, занимаемые одной молекулой уксусной кислоты при данной концентрации, вычисляем по уравнению (5.11):

S₁ = = 0,25 ∙ 10^-13 см²,

S₂ = 0,21 ∙ 10^-13 см²,

S₃ = 0,11 ∙ 10^-13 см²,

S₄ = 0,06 ∙ 10^-13 см².

Тогда толщину адсорбционного слоя для Г₄ вычисляем по формуле:

δ = = 1,6 ∙ 10^-9,

где 60 – молярная масса уксусной кислоты, г/моль;

1,05 – плотность уксусной кислоты, г/см³.

Пример 3

Зависимость поверхностного натяжения водных растворов амилового спирта (С₅Н₁₁ОН) от концентрации при 25⁰С выражается следующим образом:

Концентрация, кмоль/м3	Поверхностное натяжение, мН/м
0	72,0
0,0019	70,4
0,0038	69,2
0,0075	66,7
0,0150	61,7
0,0300	55,3
0,0600	46,6
0,1200	38,0

Графическим способом определите величину адсорбции амилового спирта из раствора с концентрацией 0,030 кмоль/м³.

Решение.

Построим график зависимости поверхностного натяжения от концентрации. Проведем касательную к кривой в стыке, имеющей ординату 0,030 кмоль/м³. Тангенс угла наклона касательной к оси абсцисс равен .

Из графика находим:

= -0,495 Н/м² кмоль.

Множитель 10^-3 в числителе связан с тем, что σ в таблице и на рис. выражено в мН/м. По уравнению изотермы адсорбции Гиббса находим:

Г = = 5,95∙10^-9 кмоль/м².

Пример 4

Рассчитайте количество ммоль аммиака, адсорбированное 100 г почвы, если равновесное количество NH₃ равно 12,5 ммоль/л, а константы К и 1/n, определенные экспериментально, соответственно равны 5,01 и 0,30.

Решение.

Расчеты производятся по уравнению Фрейндлиха, представленного в логарифмической форме: . Подставляя числовые данные, получим: lgХ = 0,70 + 0,3291 = 1,0291, Х = 10,69 ммоль/100 г.