2.8. Представление звуковой информации в памяти пк

Звук представляет собой звуковую волну с непрерывно меняющейся амплитудой и частотой. Чем больше амплитуда сигнала, тем он громче, чем больше частота, тем выше тон. Для того, чтобы компьютер мог обработать звук, он должен быть превращен в последовательность электрических импульсов (двоичных нулей и единиц).

В процессе кодирования непрерывного звукового сигнала производиться его временная дискретизация. Непрерывная звуковая волна разбивается на отдельные маленькие временные участки, при чем для каждого участка устанавливается определенная величина амплитуды.

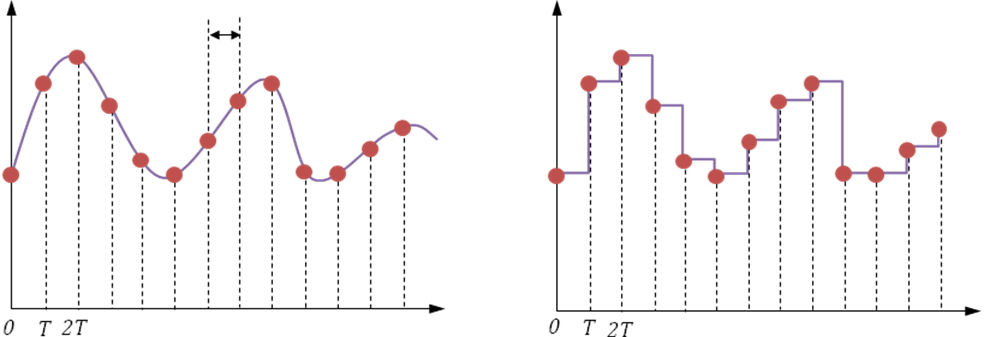
При двоичном кодировании непрерывного сигнала он заменяется последовательностью дискретных уровней сигнала. Качество кодирования зависит от количества измерений уровня сигнала в единицу времени, т. е. частоты дискретизации. Чем большее количество измерений производиться за одну секунду, тем точнее процедура двоичного кодирования.

2.9. Обобщение по теме «Арифметические основы вт»

Задание 50. Ответьте на вопросы теста.

1. В позиционных системах счисления значение числа...

а) зависит от положения цифр в нем; в) вычисляеться по специальным правилам;

б) независит от положения цифр в нем; г) обозначаеться специальными знаками.

2. Выберете верное утверждение:

а) VI = 5; в) MMLV = 2055;

б) MDXIX = 2519; г) MCMXCVIII = 2213.

3. Набор цифр, с помощью которых записываются числа:

а) система счисления; в) основание системы счиления;

б) алфавит системы счисления; г) разрядность системы счисления.

4. Число 21₁₆ соответствует числу в десятичной системе счисления:

а) 64₁₀; в) 32₁₀;

б) 1010₁₀; г) 33₁₀.

5. Число 10000011₂ соответствует числу в шестнадцатиричной системе счисления:

а) 84₁₆; в) 83₁₆;

б) 87₁₆; г) 86₁₆.

6. Укажите самое большое число:

а) 16₁₃; в) 16₈;

б) 16₁₀; г) 16₁₆.

7. Какое число соответствует дополнительному коду числа –111:

а) 00010001; в) 10000111;

б) 10000001; г) 10010001.

8. Положение запаятой в формате с плавающей запятой указывает:

а) мантисса числа; в) алфавит системы счисления;

б) основание системы счисления; г) порядок.

Тема 3. Логические основы вт

3.1. Основные понятия алгебры логики

Основы логики заложил Аристотель, который впервые отделил логические формы мышления от его содержимого.

Логика — это .............................................................................................................................

В 1847 г. английский математик Джордж Буль опубликовал статью «Математический анализ логики». Буль указал на возможность применения математических операций (сложение, умножение) к логическим высказываниям.

Алгебра логики (булева алгебра) — это .............................................................................. ................................................................................................................................................................................................................................................................................................................................

Основным понятием алгебры логики является высказывание.

Высказывание — это ............................................................................................................... ................................................................................................................................................................................................................................................................................................................................

Задание 1. Какие из предложений являются высказываниями? Определите их истинность.

1. Число 6 — четное. ......................................................................

2. Посмотрите на доску. ......................................................................

3. Все роботы являются машинами. ......................................................................

4. У каждой лошади есть хвост. ......................................................................

5. Внимание! ......................................................................

6. Кто отсутствует? ......................................................................

7. Есть кошки, которые дружат с собаками ......................................................................

8. Не все то золото, что блестит. ......................................................................

9. x² > 0. ......................................................................

10. Некоторые люди являются художниками ......................................................................

11. Выразите 1 час 15 минут в минутах ......................................................................

12. Всякий моряк умеет плавать. ......................................................................

Задание 2. Придумайте и запишите предложения, удовлетворяющие следующим условиям.

1. Истинное высказывание: .......................................................................................................

2. Ложное высказывание: .......................................................................................................

3. Не высказывание: .......................................................................................................

Для использования в логических выражениях высказывания обозначают буквами латинского алфавита.

Пример:

А = {Лед — твердое состояние воды}

B = {Треугольник — это геометрическая фигура}

C = {Париж — столица Китая}

Любое высказывание может быть истинным (1) или ложным (0).

Пример: А = 1, B = 1, C = 0

Высказывания могут быть простыми и составными. Простыми называют высказывания, состоящие из одного утверждения.

Составное высказывание — ................................................................................................. ................................................................................................................................................................ ................................................................................................................................................................

В качестве связок могут выступать «и», «или», «не», «если ..., то ...», «тогда и только тогда, когда».

Задание 3. Составьте сложные высказывания, используя логические связки.

A = {Сейчас идет дождь}.

B = {Форточка открыта}.

A и B

................................................................................................................................................................

A или не B

................................................................................................................................................................

если A, то B

................................................................................................................................................................

не A и B

................................................................................................................................................................

A тогда и только тогда, когда B

................................................................................................................................................................

................................................................................................................................................................

Задание 4. Составьте сложные высказывания, используя логические связки.

А = {Работник хорошо работает} Р. — работник,

B = {У работника хорошая зарплата} з. п. — зарплата.

A и B

................................................................................................................................................................

A или не B

................................................................................................................................................................

если A, то B

................................................................................................................................................................

не A и B

................................................................................................................................................................

A тогда и только тогда, когда B

................................................................................................................................................................

................................................................................................................................................................