Форматы представления чисел
В ЭВМ для представления дробных чисел применяется чаще всего одна из двух форм представления чисел: с фиксированной запятой (точкой) или с плавающей запятой (точкой).
Числа представляются в машинном слове, имеющем для конкретной ЭВМ всегда фиксированное число разрядов (битов). Это число является одной из важнейших характеристик любой ЭВМ и называется разрядностью машины.
В числах с фиксированной запятой положение запятой в разрядной сетке машины заранее обусловлено для всех чисел раз и навсегда. Место запятой, отделяющей целую часть числа от дробной, определяется на этапе конструирования ЭВМ. Сразу же указывается количество разрядов, отводимых для изображения целой и дробной частей, при этом целая и дробная части хранятся отдельно друг от друга.
Единственной особенностью, о которой необходимо упомянуть, является ситуация, которая носит название «переполнение разрядной сетки» (переполнение с фиксированной запятой) и которая возникает, когда результат умножения превышает максимально возможное для данной разрядности значение. Эта ситуация считается в ЭВМ исключительной. При ее возникновении записать получившееся значение невозможно. В этом случае устанавливается в «1» специальный флаг переполнения, старший бит результата (бит переноса из старшего разряда слова) теряется, а в качестве результата выдается искаженное число. Описываемая ситуация не считается критической, и после окончания данной операции вычисления продолжаются.
Иначе обстоит дело с операцией деления. При делении целого числа на другое целое результат совсем не обязательно должен быть целым. А поскольку и результат должен быть представлен целым числом, возникает коллизия (противоречие).
Таким образом, форма с фиксированной запятой приводит к некоторым неудобствам. При работе с ней постоянно приходится следить за правильным и эффективным использованием разрядной сетки, чтобы числа не выходили за старший разряд и в то же время, чтобы старшие разряды использовались как значащие. Основное преимущество данной формы — простота арифметических операций, недостаток — слишком узкий диапазон представления чисел.
-
Цела часть:
27
26
25
24
23
22
21
20
,
Дробная часть:
20
2-1
2-2
2-3
2-4
2-5
2-6
2-7
Для того чтобы автоматизировать действия по эффективному использованию всей разрядной сетки, а также значительно увеличить диапазон изображения чисел, в ЭВМ введена еще одна форма представления чисел — с плавающей точкой.
,
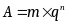где
m — мантисса числа,
q — основание системы счисления,
n —порядок.
В форме с плавающей запятой число представляется двумя компонентами: мантиссой и порядком. Мантисса используется для записи цифр числа, а порядок — для указания положения запятой.
Форма представления чисел с плавающей запятой позволяет записывать числа из весьма широкого диапазона и с достаточно высокой точностью. Что является преимуществом данной формы. Недостатком формы представления чисел в форме с плавающей запятой является значительное усложнение арифметических операций.
Например, в десятичной системе счисления число 3,14 представим в виде:
3,14 = 0,314 101, где
мантисса равна 0,314, а порядок — 1. Очевидно, такое представление далеко не однозначно. Можно ведь 3,14 записать так:
3,14 = 3,14 100 = 31,4 10-1 = 0,0314 102 = …,
Порядок числа определяет положение запятой в записи мантиссы. При корректировке порядка соответствующим образом меняется и положение запятой — запятая как бы «плавает». Отсюда и название метода представления чисел.
Местоположение запятой при этом тоже строго фиксируется: считается, что мантисса всегда представляется как число, меньшее единицы, но такое, в котором первая цифра после запятой для всех абсолютно чисел отлична от нуля (единственное исключение составляет число 0). Такая форма представления мантиссы называется нормализованной. Иначе говорят, что мантисса нормализована (приведена к виду: 0,1 < m ≤ 1), например, для числа 3,14 нормализованная форма будет выглядеть так:
3,14 = 0,314 101.
Пример: Записать число 410 в 24-разрядной ячейке в форме с плавающей запятой.
410
= 1002
= 0,1002
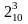= 0,1002
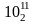
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
Знак числа |
Знак порядка |
Порядок |
Мантисса |
|||||||||||||||||||||
Пример: Записать число –9,510 в 24-разрядной ячейке в форме с плавающей запятой.
–9,510
= –1001,12
= –0,10011
=–0,10011
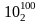
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
|
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
Знак числа |
Знак порядка |
Порядок |
Мантисса |
|||||||||||||||||||||
Задание 33. Записать числа в нормальной форме с плавающей запятой в 24-разрядной ячейке.
а. 1010 = ........................................................................................................................................
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б. –15,310 = ...................................................................................................................................
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в. 0,0510 = .....................................................................................................................................
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
г. –6,2510 = ...................................................................................................................................
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
д. 3,1810 = .....................................................................................................................................
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е. –0,12510 = .................................................................................................................................
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ж. –15,110 = ..................................................................................................................................
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
з. –23,510 = ...................................................................................................................................
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и. –55,5510 = .................................................................................................................................
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|