Интерполяция лагранжа, ньютона.

Если заданы n+1 узлов ( ) , , то можно через указанные точки построить интерполяционный полином степени «n» вида

1. , где вспомогательные полиномы Лагранжа.

2. , где

Для уменьшения неустойчивости интерполяционных полиномов применяют расположение точек по закону нулей Чебышева

Наиболее точное приближение функции дает интерполяция сплайнами.

В пакете Mathcad имеются следующие стандартные функции для интерполяции:

linterp(VY,VY,x)- функция для кусочно-линейной интерполяции . VX, XY-массивы узловых точек - соответственно, x- значение аргумент;

cspline(VX,VY)-вспомогательная функция для вычисления массива VS вторых производных при интерполяции кубическими сплайнами;

interp(VS,VX,VY,x)- интерполяционный полином при сплайн-аппроксимации.

В пакете Maxima имеются следующие стандартные функции для интерполяции:

load(interpol) — функция загружает пакет Interpol;

f(x):=linearinterpol(m,varname='x) — формирует функцию f(x) для кусочно линейной интерполяции,

g(x):=cspline(m,varname='x) — интерполяционный полином при сплайн-аппроксимации, где m — матрица из двух столбцов узловых точек , которую можно сформировать из списков узловых точек:

m:transpose(matrix(x,y)).

Контрольные задания

1. Построить в логарифмическом масштабе графики функций

2. Определить, какой одной из двух возможных функциональных зависимостей принадлежат данные из файлов El.prn,..., E10.prn. Найти значение l. (Данные в файлах записаны попарно (x,y) для каждой точки графика).

3. Построить интерполяционные полиномы Лагранжа для зависимостей из файлов Lag1.prn..Lag10.prn.

4. Рассмотреть пример Рунге. Построить интерполяционные полиномы Лагранжа с равномерной сеткой, с узлами Чебышева. Использовать интерполяцию сплайнами.

5. Найти обратные функции для данных, имеющих функциональные зависимости

a) F(x)=1-exp(-x^c) b) F(x)=arctg((x-a)/c) c) F(x)=((x-m)/) d) F(x)=1-1/(1+x^2k) e) f) F(x)=arcsin(x/c) g) F(x)=1-1/(x/c)^k

6. При помощи вероятностной бумаги определить, к какому типу распределения – нормальному или релеевскому принадлежат функции распределения, записанные в файлах Paper1.prn,…Paper 10.prn.

Примеры выполнения заданий в пакете maxima

1. Построить в логарифмическом масштабе график функции .

(%i1) plot2d([exp(-x^2)], [x,-4,4],[y,1e-5,1],[logy])$

или

(%i1) wxplot2d([exp(-x^2)], [x,-4,4], [y,1e-5,1], [gnuplot_preamble, "set logscale y; set grid;"])$

2. Определить, какой одной из двух возможных функциональных зависимостей принадлежат данные из файла E0.prn. Найти значение l.

file_search("d:/E0.prn");

printfile("d:/E0.prn");

data:read_nested_list("d:/E0.prn");

n:length(data);

x:makelist(first(data[i]),i,1,length(data));

y:makelist(second(data[i]),i,1,length(data));

wxplot2d([discrete,x,y],[style,[points,3]]);

f(x):=-log(1-x);

g(t):=sqrt(-log(1-t));

ff:map(f,y),numer;

gg:map(g,y),numer;

wxplot2d([[discrete,x,ff],[discrete,x,gg]],[gnuplot_preamble, "set grid;"]);

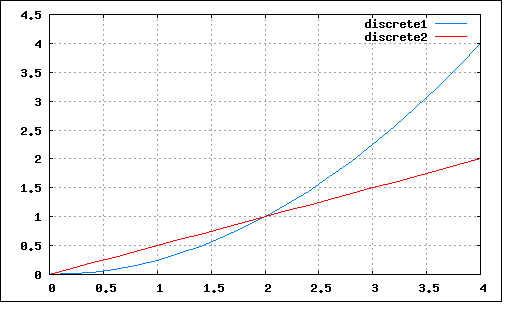
Из рисунка видно, что вторая из предложенных зависимостей удовлетворяет исходным данным, считанным из файла. Тангенс угла наклона приямой равен .

3. Построить интерполяционные полиномы Лагранжа для зависимостей, заданных точками , .

n:5;

x:makelist(i*0.5, i, 0, n);

f(t):=1+1.8*t-t^3;

y:map(f,x),numer;

L(u,k,n):=block([p,i,c],

p:1,for i:1 thru n+1 do block(c:if k=i then 1 else (u-x[i])/(x[k]-x[i]),

p:p*c),

p:p);

Pn(u):=sum(y[k]*L(u,k,n),k,1,n+1);

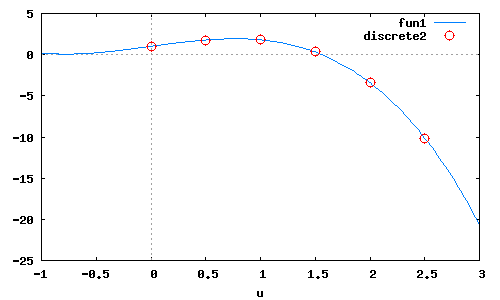
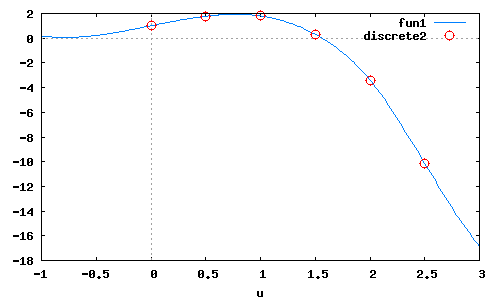
wxplot2d([Pn(u),[discrete,x,y]],[u,-1,3],[style,[lines],[points]]);

Результат интерполяции полиномами Лагранжа

load(interpol);

m:transpose(matrix(x,y));

fit(u):=linearinterpol(m,varname='u);

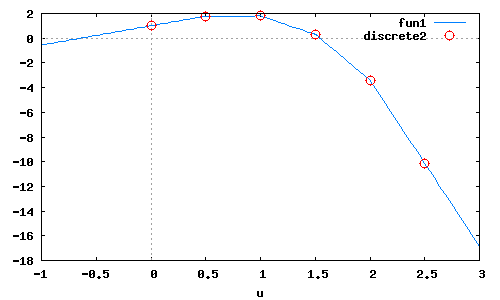
wxplot2d([fit(u),[discrete,x,y]],[u,-1,3],[style,[lines],[points]]);

Кусочно-линейная интерполяция

fsp(u):=cspline(m,varname='u);

wxplot2d([fsp(u),[discrete,x,y]],[u,-1,3],[style,[lines],[points]]);

Интерполяция сплайнами

4. Рассмотреть пример Рунге. Построить интерполяционные полиномы Лагранжа с равномерной сеткой, с узлами Чебышева. Использовать интерполяцию сплайнами.

n:8; a:-1; b:1; dx:(b-a)/8;

f(t):=1/(1+25*t^2);

сначала зададим равномерную сетку

x:makelist(a+i*dx, i, 0, n),numer;

y:map(f,x),numer;

строим интерполяционный многочлен

L(u,k,n):=block([p,i,c],

p:1,for i:1 thru n+1 do block(c:if k=i then 1 else (u-x[i])/(x[k]-x[i]),

p:p*c),

p:p);

Pn(u):=sum(y[k]*L(u,k,n),k,1,n+1);

wxplot2d([Pn(u),[discrete,x,y]],[u,-1,1],[style,[lines],[points]]);

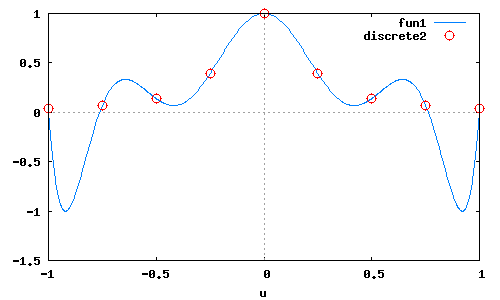
Зададим сетку на основе узлов Чебышева

xx:makelist(cos(%pi*(2*i+1)/(2*(n+1))), i, 0, n),numer;

yy:map(f,x),numer;

L(u,k,n):=block([p,i,c],

p:1,for i:1 thru n+1 do block(c:if k=i then 1 else (u-xx[i])/(xx[k]-xx[i]),

p:p*c),

p:p);

Pn(u):=sum(yy[k]*L(u,k,n),k,1,n+1);

wxplot2d([Pn(u),[discrete,xx,y]],[u,-1,1],[style,[lines],[points]]);

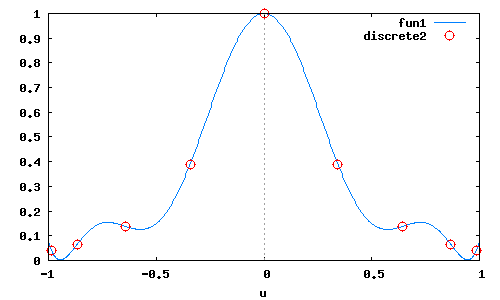
Воспользуемся интерполяцией сплайнами

load(interpol);

m:transpose(matrix(x,y));

fsp(u):=cspline(m,varname='u);

wxplot2d([fsp(u),[discrete,x,y]],[u,-1,1],[style,[lines],[points]]);