2. Показатели безотказности восстанавливаемых систем.

В пределах любого i–ого интервала безотказной работы восстанавливаемой системы справедливы все показатели безотказности, рассмотренные ранее для невосстанавливаемых систем (P(t), Q(t), ƒ(t), λ(t), T₀). Кроме этих показателей безотказности используются дополнительные показатели безотказности, которые учитывают процессы отказов и восстановлений характерные именно для восстанавливаемых систем. К числу таких показателей относятся следующие показатели:

1) параметр потока отказов ω(t):

, (2)

где M[n(t + Δt)] и M[n(t)] – математическое ожидание числа отказов n за время t + Δt и t соответственно.

Из выражения (2) можно записать следующую формулу:

a’(t) = w(t) (3)

Умножим обе части уравнения (3) на dt и проинтегрируем их:

, (4)

(5)

Для стационарного потока отказов параметр потока отказов w(t) будет являться постоянной величиной, то есть w(t) = w = const. Тогда формула (5) примет вид:

a(t) = w · t (6)

Статистически, то есть по результатам испытаний, параметр потока отказов определяется по следующей формуле:

, (7)

где n_i(Δt) – суммарное число отказов i – ого испытуемого образца на интервале времени Δt (от t до t + Δt);

- суммарное число отказов, возникших во всех N₀ объектах на интервале времени Δt (от t до t + Δt).

Так как 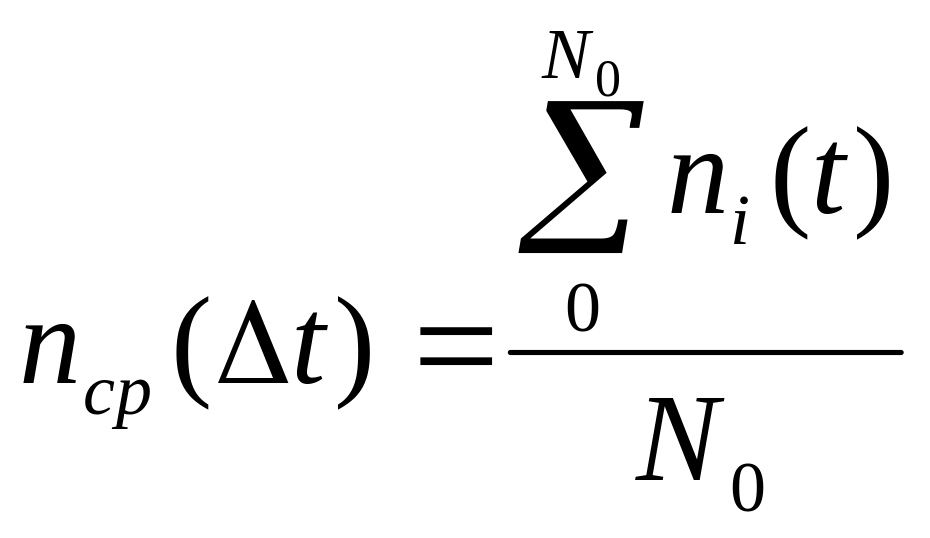- среднее число отказов на интервале Δt, приходящееся на один испытуемый образец. Поэтому формулу (7) можно записать так:

.

Интенсивность отказа определяется по следующей формуле:

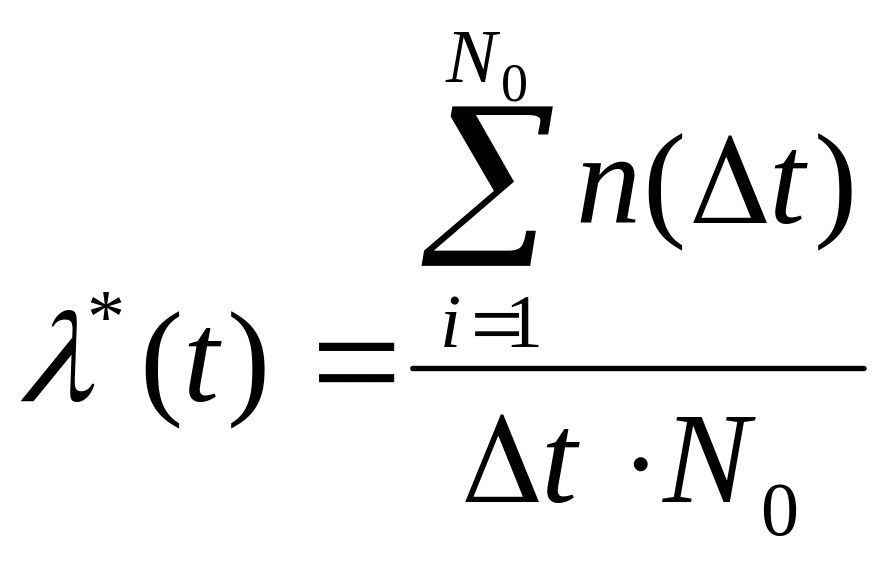[1/ч].

2) средняя наработка на отказ (T_cp = T_p.cp ) – это среднее время безотказной работы восстанавливаемого объекта между двумя соседними отказами.

Для восстанавливаемых систем средняя наработка до отказа определяется по следующим формулам:

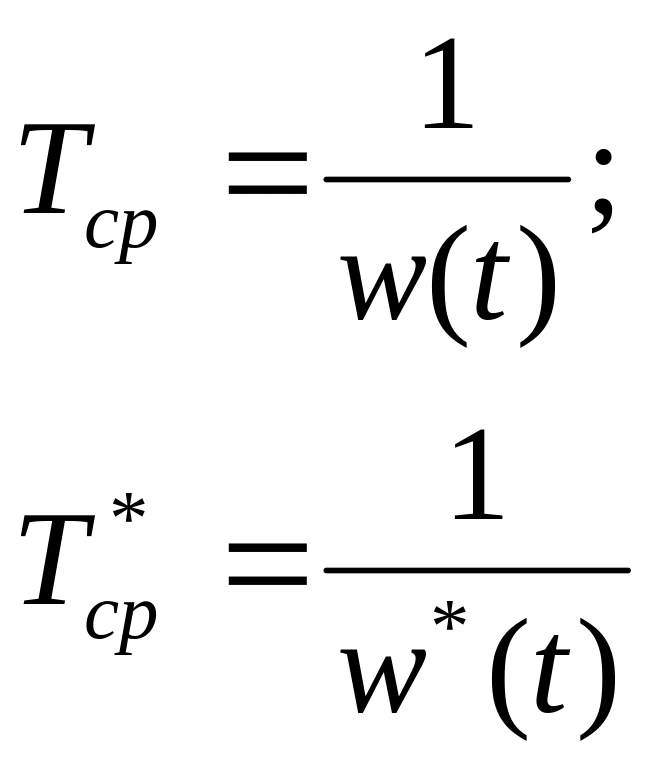(8).

Так как для простейшего потока отказов w(t) = w = const, то формулу (8) можно записать в виде:

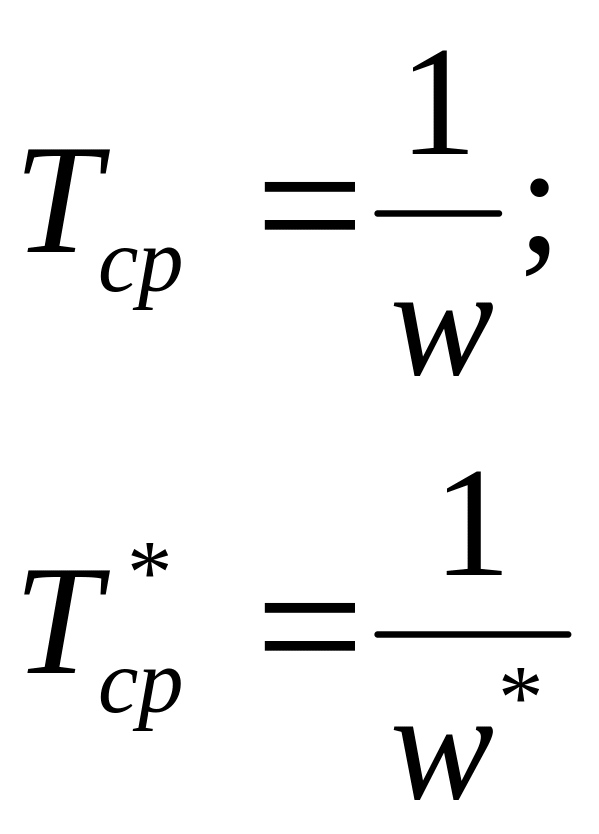(9).

Статистически средняя наработка на отказ вычисляется по следующей формуле:

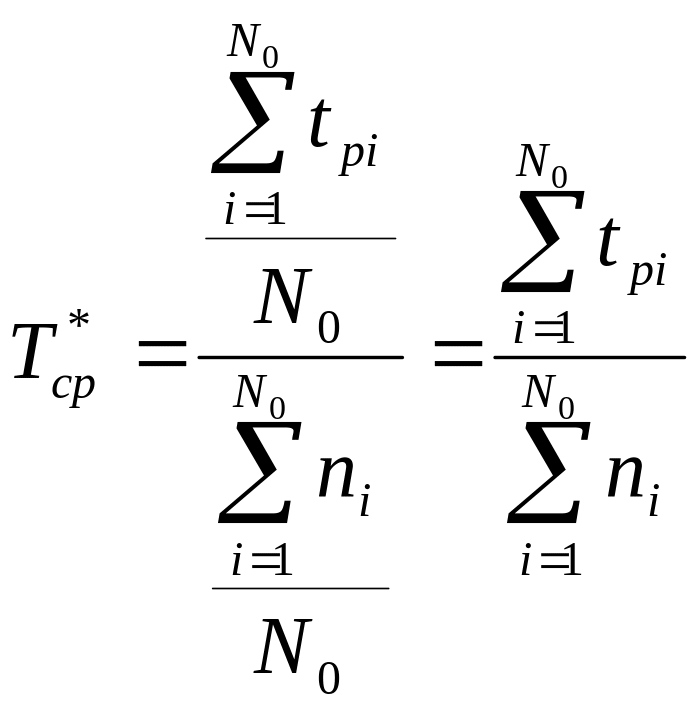[ч], (10)

где t_pi – суммарное время безотказной работы i – ого испытуемого образца;

_pi – суммарное время безотказной работы всех испытуемых образцов;

n_i – суммарное число отказов i – ого образца.

3) вероятность появления некоторого числа отказов на интервале времени (0,t) P_n(t).

Выражение для этой вероятности получим путем подстановки в формулу (1) значение a(t) = wt. Тогда эта формула примет следующий вид:

(11)

Формула (11) определяет появление требуемого числа отказов на интервале времени (0,t). В этой формуле n принимает значения n = 1, 2, …

Если число отказов в восстанавливаемом объекте n = 0, то формула (11) примет следующий вид:

(12).

Формула (12) характеризует вероятность безотказной работы восстанавливаемой системы (объекта) за время t.

3. Показатели ремонтопригодности.

Показатели ремонтопригодности характеризуют процесс восстановления таких систем (их работоспособного состояния).

К числу таких показателей относят следующие:

1) P_в(t) – вероятность восстановления работоспособного состояния объекта за время t.

Математически эта вероятность определяет вероятность того, что время восстановления работоспособного состояния τ_в будет меньше наперед заданной величины t, то есть:

P_в(t) = P {τ_в< t}

где t – требуемое время восстановления объекта, которое определяется технической документацией или представляет собой реальное время, которое может быть затрачено на восстановление.

Эта вероятность P_в(t) представляет собой интегральную функцию распределения случайной величины τ_в.

Статистическое значение вероятности P_в(t) определяется следующим образом:

, (1)

где N_в(t) – число восстановленных объектов за время t;

N_ов(t) – число отказавших объектов, которые поставлены в очередь на восстановление.

2) ƒ_в(t) – плотность вероятности восстановления работоспособного состояния объекта (частота восстановления; плотность (закон) распределения времени восстановления).

Данный показатель является дифференциальной функцией распределения случайной величины τ_в. Поэтому она определяется как производная от интегральной функции распределения:

, (2)

, (3)

где μ – интенсивность восстановления объекта.

Определим связь между характеристиками P_в(t), ƒ_в(t) и μ.

Из формулы (2) можно записать:

(4)

Проинтегрируем обе части выражения (4):

,

Таким образом P_в(t) определяется:

(5)

Геометрически P_в(t) представляет собой возрастающую экспоненту:

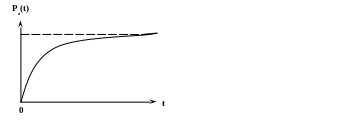
Статистическое значение плотности вероятности отказов будет определяться по следующей формуле:

, [1/ч] (6)

где N_в(Δt) – число объектов, восстанавливаемых на интервале времени Δt;

N_ов(t) – число объектов, требующих восстановления на интервале времени t.

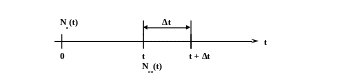
3) μ(t) – интенсивность восстановления работоспособного состояния объекта за время t.

Она определяется как условная плотность вероятности восстановления объекта в момент времени t при условии, что до этого момента времени t восстановление объекта не произошло.

.

В период нормальной эксплуатации объекта (то есть для экспоненциального закона восстановления) характеристика μ(t) является величиной постоянной μ(t) = μ = const. Точное значение характеристики μ определяется по следующей формуле:

, [1/ч] (7)

где Т_в – среднее время восстановления работоспособного состояния системы.

Статистически интенсивность восстановления μ определяется по следующей формуле:

, (8)

где N_ов(t) – N_в(t) – число невосстановленных объектов за время t.

4) Т_в – среднее время восстановления объекта.

Оно определяется как математическое ожидание случайной величины τ_в:

, (9)

. (10)

Интеграл (10) приведем к табличному виду и запишем его:

∫UdV = UV - ∫VdU

Введем следующие обозначения: t = U, dP_в(t) = dV, dt = dU, V = P_в(t). Тогда формулу (10) запишем в виде:

(11)

В формуле (11) произведение t·P_в(t) можно заменить единицей, так как при t→ ∞ вероятность P_в(t→ ∞) будет стремиться быстрее, чем t будет стремиться к ∞. Поэтому точное значение средней наработки до отказа будет равно:

. (12)

Определим связь между характеристиками Т_в и μ. Для этого воспользуемся формулой (11), в которую подставим вместо вероятности Р_в(t) ее значение 1- е ^-μ·t:

.

При t→ ∞ произведение t·е ^-μ·t можно заменить нулем, так как экспонента е ^-μ·t будет стремиться к нулю быстрее, чем t будет стремиться к бесконечности. Таким образом:

(13).

По результатам испытаний приближенное значение характеристики Т_в определяется по формуле:

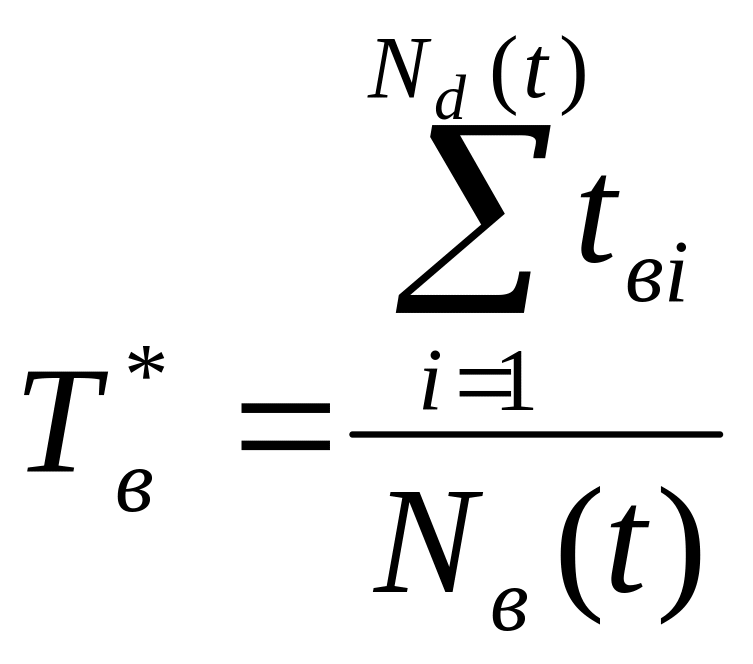, (14)

где t_вi – суммарное время, затраченное на восстановление работоспособного состояния i - ого испытуемого объекта.

Для восстановления систем число восстановлений равно числу отказов, и каждый испытуемый объект может иметь за время t несколько отказов. Поэтому характеристику Т^*_в можно вычислять по следующей формуле:

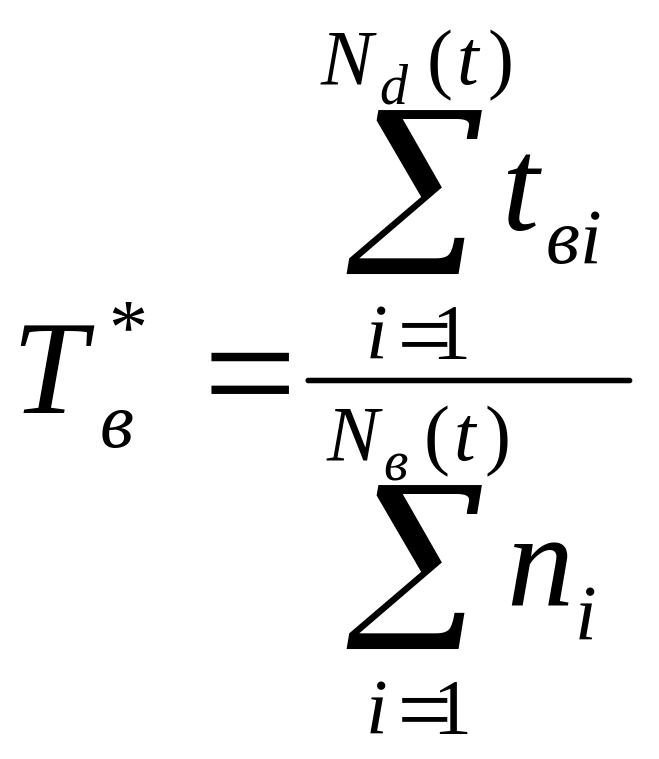, (15)

где n_i – это суммарное число отказов, возникших у i – ого объекта за время испытаний t.

Формула (15) определяет среднее время восстановления, затрачиваемое на один отказ на один восстановленный объект. В формуле (15) верхние пределы в суммах можно заменить общим числом объектов N₀, поставленных на испытание. Поэтому для неотказавших объектов соответствующие значения t_вi и n_i можно заменить нулем. Тогда:

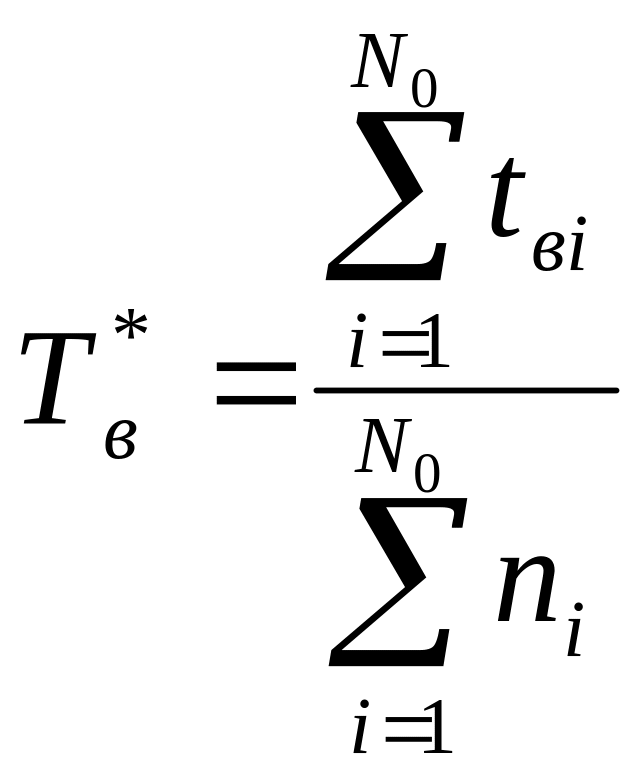. (16)

Формула (16) определяет характеристику Т_в^* как среднее время, затрачиваемое на восстановление одного отказа в одном объекте.