Тема 3. Расчет надежности нерезервированных восстанавливающих систем.

1. Потоки отказов и восстановлений восстанавливающих нерезервированных систем.

Для восстанавливающих систем характерно восстановление их работоспособного состояния. Как правило, системы АТС являются восстанавливаемыми. Процесс эксплуатации таких систем можно изобразить в виде такой диаграммы (рис. 1):

t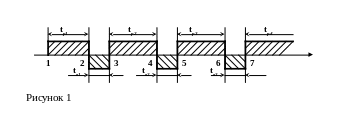

t_pi (i=1,2,3,4, ... ) – интервалы времени, в течение которых система работает без отказа;

точки 2, 4, 6 – моменты времени, в которых происходят отказы систем;

t_вi (i = 1, 2, 3, ... ) – интервалы времени, в течение которых осуществляется восстановление работоспособного состояния системы;

точки 1, 3, 5, 7 – моменты времени, в которые осуществляется восстановление работоспособного состояния и включение системы в работу.

Из рисунка 1 видно, что для таких систем характерно чередование периодов безотказной работы и периодов восстановления, причем длительность этих периодов является случайной величиной. Сам процесс эксплуатации таких систем можно рассматривать как совокупность двух процессов: случайного процесса отказа и случайного процесса восстановления. И тот, и другой процессы представляют собой потоки случайных событий:

1) поток отказа с интенсивностью λ;

2) поток восстановления с интенсивностью μ.

Рассмотрим сначала свойства потока отказа. Для систем, работающих в период нормальной эксплуатации, поток отказа является простейшим. Простейшим называется поток, удовлетворяющий одновременно трем условиям:

1) ординарности;

2) отсутствию последствия;

3) стационарности.

Рассмотрим эти условия.

Ординарность потока отказов выражает условие практической невозможности появления двух или более отказов за достаточно малый промежуток времени Δt:

.

Отсутствие последствия состоит в том, что вероятность появления некоторого числа отказов n в течение произвольного промежутка времени Δt не зависит от того, сколько было отказов, и как часто они возникали до этого промежутка: P_n(Δt). Ординарный поток без последствия называют Пуассоновским, так как вероятность появления n отказов на интервале времени (0, t) определяется законом Пуассона, то есть:

, (1)

где a(t) = M[n(t)] – математическое ожидание числа отказов n на интервале времени (0, t).

Стационарность потока отказов означает, что вероятность возникновения некоторого числа отказов n за промежуток времени Δt ( от t до t + Δt) P_n(Δt) не зависит от момента времени t, а зависит от длины временного интервала Δt и от числа отказов n. Это можно проиллюстрировать графиком:

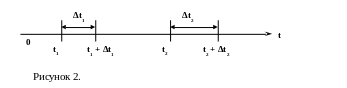
P_n(Δt₁) = P_n(Δt₂) при условии, что Δt₁ = Δt₂.

Поток восстановлений работоспособного состояния также является простейшим и удовлетворяет трем перечисленным выше условиям. Надежность восстанавливаемых систем включает в себя два частных свойства:

1) свойство безотказности, связанное с потоком отказов;

2) свойство ремонтопригодности, связанное с потоком восстановления.

Поэтому для оценки надежности восстанавливаемых систем используют три вида показателей:

1. показатели безотказности;

2. показатели ремонтопригодности;

3. комплексные показатели, учитывающие одновременно и безотказность, и ремонтопригодность.

Рассмотрим эти виды показателей надежности.