5. Расчет надежности невосстанавливаемых нерезервированных систем.

Для таких систем ССН будет иметь следующий вид (рис. 1):

N – общее число элементов, которые входят в состав нерезервированной системы.

В этом случае, если один элемент отказывает, то отказывает вся система. Вероятность безотказной работы определяется по формуле:

,

где - интенсивность отказов системы;

- вероятность безотказной работы i – ого элемента.

Средняя наработка до отказа определяется по формуле:

.

6. Расчет надежности невосстанавливаемых систем с постоянным общим резервированием.

Допущения при расчете надежности таких систем следующие:

1) отказы элементов в основной и резервной системах являются независимыми событиями;

2) отказы систем также являются независимыми;

3) изменение нагрузки не влияет на надежность ( то есть k_н ≤ 1 ).

ССН при постоянном общем резервировании имеет следующий вид (рис.1):

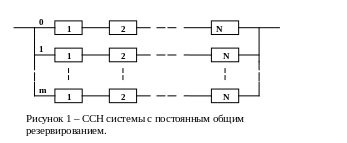
0 – основная система, состоящая из N элементов;

1 ÷ m – резервные системы, каждая из которых состоит из N элементов.

В общем случае основная и резервные системы могут быть различными, хотя выполняют одни и те же функции.

P₁(t), P₂(t), ... , P_N(t) – вероятности безотказной работы элементов;

P₀(t) и Q₀(t) = 1 – P₀(t) – вероятности безотказной работы и отказа основной системы;

P₁(t), ... , P_m(t); Q₁(t), ... , Q_m(t) – вероятности безотказной работы и отказа соответствующих резервных систем.

Так как основная и резервные системы при этом способе резервирования соединены параллельно, то отказ всей резервной системы произойдет тогда, когда откажут и основная и все резервные системы. Поэтому вероятность отказа системы равна:

.

(1)

Если основная и резервные системы являются одинаковыми системами, то все системы будут равнонадежными, то есть

P₀(t) = P₁(t) = P₂(t) = ... = P_m(t), то формула (1) примет следующий вид:

P_c(t) = 1 – [1 – P₀(t)]^m+1 (2).

P₀(t) – вероятность безотказной работы основной и резервной системы.

Учитывая, что вероятность P₀(t) = е ^{– λ}₀^t , где - интенсивность отказов основной или любой резервной системы; λ_i – интенсивность i – ого элемента, получим:

P_c(t) = 1 – [1 – e ^{– λ}₀^t]^m+1 (3)

Определим среднюю наработку до отказа резервированной системы для случая, когда основная и резервная системы являются равнонадежными.

(4).

Введем следующие обозначения: 1 – e ^{– λ}₀^t = z (5). Тогда e ^{– λ}₀^t = 1-z .

Возьмем дифференциал от обеих частей:

dz = d[1 – e ^{– λ}₀^t] = [1 – e ^{– λ}₀^t]^’dt.

Выразим из последнего уравнения производную [1 – e ^{– λ}₀^t]^’ = λ₀ e ^{– λ}₀^t. Тогда:

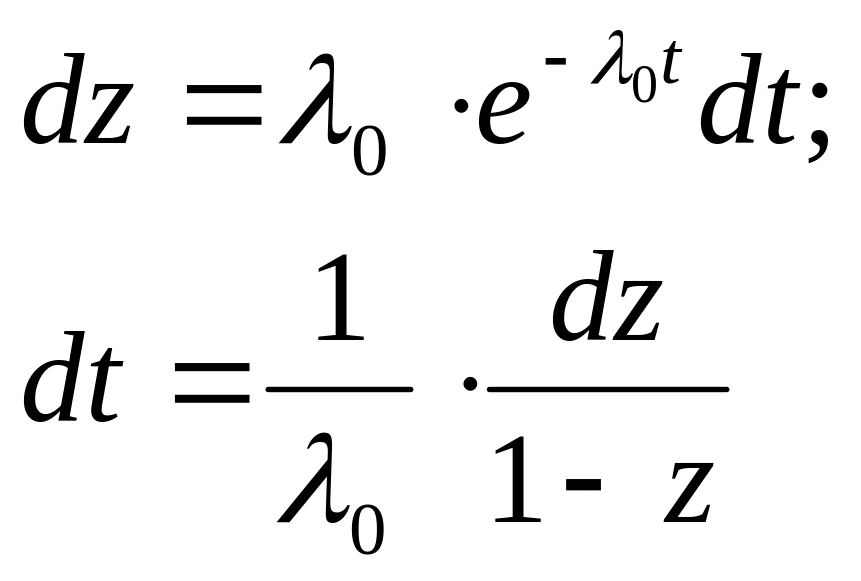(6)

Подставим выражение (6) и выражение (5) в формулу (4) и получим:

(7).

В формуле (7) пределы интегрирования взяты от 0 до 1, так как введенная переменная z , равная : 1 – e ^{– λ}₀^t = z, будет изменяться в пределах от 0 до 1. Интеграл (7) не является табличным. Выполним деление:

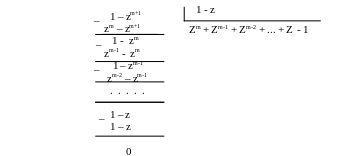
Подставим в формулу (7) полученное частное и получим :

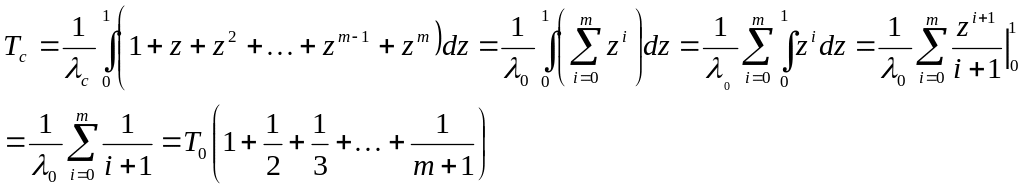
Т₀ – средняя наработка до отказа основной или любой резервной системы.

Е сли все системы различны, то средняя наработка системы до отказа будет определяться по формуле:

.