2. Оформление расчетно-графической работы

Расчетно-графическая работа должна иметь следующий состав: титульный лист, содержание, введение, задача № 1, задача № 2, …, задача № 5, заключение, список использованных источников. Пример оформления титульного листа расчетно-графической работы приведен в приложении А.

Графический материал работы оформляются в виде рисунков в составе соответствующих задач.

Расчетно-графическая работа выполняется на листах писчей бумаги формата А4 (210×297 мм) с полями по всем четырем сторонам листа (без рамки). Размеры левого поля – не менее 30 мм, верхнего и нижнего – не менее 20 мм, правого – не менее 10 мм. Текст работы выполняется на одной стороне листа: пишется от руки (высота букв и цифр должна быть не менее 2,5 мм) или печатается с использованием компьютера и принтера (размер шрифта – не менее 12 пт).

Общий объем расчетно-графической работы: 10 – 20 листов формата А4. Листы работы должны быть пронумерованы (за исключением титульного листа и содержания).

Расчетно-графическая работа должна быть оформлена в соответствии с требованиями ГОСТ ЕСКД и СТП РГУПС.

При наличии замечаний исправления делаются на чистой стороне листа (оборотной стороне предыдущего листа) рядом с допущенной ошибкой.

3. Задание на расчетно-графическую работу

Целью расчетно-графической работы является закрепление теоретических сведений и получение практических навыков по расчету надежности систем обеспечение движения поездов.

Перед выполнением расчетно-графической работы необходимо изучить теоретические основы, изложенные в разделе 1; ознакомиться с рекомендуемой литературой, перечень которой указан в конце настоящих методических указаний.

Расчетно-графическая работа включает в себя 5 (пять) задач. Решение задач рекомендуется выполнять в той же последовательности, как они поставлены.

Указания по выбору варианта содержаться в условии каждой задачи.

Для каждой задачи приведен типовой пример ее решения.

Задача № 1 На испытание поставлено N₀ однотипных изделий. За время t часов отказало n(t) изделий. За последующий интервал времени Δt отказало n(Δt) изделий. Необходимо вычислить статистические значения вероятности безотказной работы за время t и t+Δt, частоты отказов и интенсивности отказов за время t. Исходные данные для решения задачи приведены в табл. 3.1. Номер варианта определяется двумя последними цифрами номера зачетной книжки студента.

Таблица 3.1

Предпоследняя цифра номера	Последняя цифра номера	N0	t, час	Δt	n(t)	n(Δt)
1	2	3	4	5	6	7
Четная или 0	1	1000	8000	1000	290	50
	2	1000	14000	1000	540	50
	3	100	5000	100	10	10
	4	100	4000	200	20	20
	5	100	3000	1000	20	20
	6	1000	800	100	216	15
	7	1000	2300	100	417	13
	8	1000	1200	100	274	14
	9	1000	900	100	231	14
	0	1000	10000	1000	370	40
Нечетная	1	1000	15000	1000	590	40
	2	1000	21000	1000	840	50
	3	1000	11000	1000	410	40
	4	1000	1300	100	288	13
	5	1000	1900	100	368	12
	6	1000	2700	100	480	25
	7	100	6000	500	50	20
	8	100	4000	1000	10	6
	9	100	10000	1000	25	5
	0	1000	1400	100	301	14

Типовой пример. На испытание поставлено = 2000 однотипных изделий. За время = 4000 часов отказало = 100 изделий, а за последующие = 100 часов отказало еще = 10 изделий (см. рис 1). Определить статистические значения показателей надежности: , ; ; ; ; .

Рис. 3.1

Решение

1. По формулам (1.1.1) и (1.1.2) определяем вероятности безотказной работы и отказа за время испытаний час:

или из формулы (1.1.3):

.

2. Определяем и за время испытаний :

или из формулы (1.1.3):

.

3. Определяем за время час по формуле (1.1.7):

1/ч.

4. Определяем за время по формуле (1.1.9):

1/ч.

Задача № 2 Структурная схема надежности устройства для различных вариантов приведена на рис. 3.2. Номер варианта определяется двумя последними цифрами номера зачетной книжки студента. Интенсивности отказов элементов имеют следующие значения: λ₁=n₁∙10^-4 1/час; λ₂=n₂∙10^-4 1/час; 1/час; 1/час, где n₁ – последняя цифра номера зачетной книжки (цифра 0 соответствует n₁=10); n₂ – предпоследняя цифра номера зачетной книжки (цифра 0 соответствует n₂=10). Показатели надежности устройства распределены по экспоненциальному закону распределения. Необходимо найти среднюю наработку до отказа устройства и вероятность его безотказной работы в течение 100 часов.

Рис. 3.2

Типовой пример. Структурная схема надежности устройства приведена на рис. 3.3. Интенсивности отказов элементов имеют следующие значения:

Рис. 3.3

λ₁=0,23∙10^-3 1/час; λ₂=0,5∙10^-4 1/час; λ₃=0,4∙10^-3 1/час. Показатели надежности устройства распределены по экспоненциальному закону распределения. Необходимо найти среднюю наработку до отказа устройства .

Решение.

1. Готовой формулы для средней наработки до отказа в рассматриваемом случае нет. Поэтому необходимо воспользоваться соотношением:

.

2. Найдем выражение для вероятности безотказной работы устройства. Очевидно, что

,

где ,

,

.

Тогда, подставляя значения , и в выражение для , получим:

.

Так как , , , то

.

3. Определяем среднюю наработку до отказа:

.

Подставляя в выражение для значение интенсивности отказов из условия задачи, получаем:

Задача № 3 Необходимо выполнить ориентировочный расчет надежности системы, состоящей из N элементов различного типа. Требуется вычислить вероятность безотказной работы системы в течение времени t и среднюю наработку до отказа системы Т_ср.

Расчет следует выполнить по данным о надежности элементов, приведенным в приложении Б.

Таблица 3.2

Наименование и количество элементов

Предпоследняя цифра номера	Резисторы R		Конденсаторы С		Диоды D		Транзисторы Т		Силовые трансформаторы, шт	Дроссели, шт	L, шт	Время работы t, час
	тип	шт	тип	шт	тип	шт	тип	шт
0	ВС-0,25	20	слюдяные	10	выпрямительные точечные германиевые	6	мощные низкочастотные	5	Nст	1	2	650
	ВС-0,5	14	танталовые	12			маломощные низкочастотные германиевые	4
	ВС-1	6
1	МЛТ-0,5	32	керамические	8	выпрямительные точечные германиевые	9	мощные низкочастотные	4	Nст	2	4	260
	МЛТ-1	19	танталовые	15			маломощные низкочастотные германиевые	11
	МЛТ-2	4
2	МЛТ-0,25	40	слюдяные	30	выпрямительные плоскостные	2	маломощные низкочастотные кремниевые	10	Nст	–	40	5000
	МЛТ-1	2	керамические	49
			танталовые	6
3	МЛТ-0,25	21	слюдяные	8	выпрямительные точечные кремниевые	16	маломощные низкочастотные кремниевые	7	Nст	2	–	2000
	МЛТ-0,5	5
	МЛТ-1	3
4	МЛТ-0,25	13	керамические	18	выпрямительные точечные германиевые	5	маломощные германиевые низкочастотные	6	Nст	3	2	250
	МЛТ-0,5	10	танталовые	3
	ПКВ-2	2
5	МЛТ-0,25	25	керамические	27	выпрямительные точечные кремниевые	10	мощные высокочастотные германиевые	10	Nст	3	5	500
	ПКВ-2	2	танталовые	6
6	ВС-0,25	16	керамические	6	импульсные точечные	16	маломощные низкочастотные германиевые	7	Nст	3	2	320
	МЛТ-1	10	танталовые	6
	МЛТ-2	3
7	МЛТ-0,5	240	слюдяные	53	выпрямительные плоскостные	57	мощные низкочастотные	69	Nст	–	47	26
	МЛТ-1	86	танталовые	13
8	МЛТ-0,5	146	бумажные	176	выпрямительные повышенной мощности	116	мощные низкочастотные	86	Nст	27	–	240
	СПО-2	3
	ПЭВ-10	5
9	МЛТ-0,25	136	керамические	176	выпрямительные точечные германиевые	47	маломощные низкочастотные германиевые	63	Nст	37	21	25
	МЛТ-0,5	96	танталовые	32
	ПКВ-2	12

Исходные данные для решения задачи приведены в табл. 3.2. Количество силовых трансформаторов N_ст соответствует последней цифре номера зачетной книжки студента (цифра 0 соответствует N_ст=10).

Номер варианта определяется двумя последними цифрами номера зачетной книжки студента.

Типовой пример. Система состоит из 14 маломощных низкочастотных германиевых транзисторов, 4 плоскостных кремниевых выпрямителей, 56 керамических конденсаторов, 168 резисторов типа МЛТ мощностью 0,5 Вт, 1 силового трансформатора, 2 накальных трансформаторов, 6 дросселей и 3 катушки индуктивности. Необходимо найти вероятность безотказной работы системы в течение t=260 час и среднюю наработку до отказа системы Т_с.

Решение.

1. Для выполнения ориентировочного расчета надежности составим и заполним табл. 3.3, вычислив величину интенсивности отказов изделия. Значения интенсивностей отказов λ_i элементов (графа 4) выбирается из таблиц приложения Б.

Таблица 3.3

Наименование и тип элемента	Обозначение на схеме	Количество элементов Ni	Интенсивность отказов, 10-5 1/час	Ni ∙ λi × 10-5, 1/час	Примечание
1	2	3	4	5	6
1. Транзистор маломощный низкочастотный кремневый	VT1 – VT14	14	0,3	4,2	Табл. Б.3
2. Диод выпрямительный плоскостной	VD1 –VD4	4	0,5	2	Табл. Б.3
3. Конденсатор керамический	C1 – C56	56	0,14	7,84	Табл. Б.2
4. Резистор МЛТ, 0,5 Вт	R1 – R168	168	0,05	8,4	Табл. Б.1
5. Трансформатор силовой	Т1	1	0,3	0,3	Табл. Б.4
6. Трансформатор накальный	Т2, Т3	2	0,2	0,4	Табл. Б.4
7. Дроссель	L1 – L6	6	0,1	0,6	Табл. Б.4
8. Катушка индуктивности	L7 – L9	3	0,05	0,15	Табл. Б.4

2. Вычисляем суммарную интенсивность отказов системы:

.

3. Вычисляем вероятности безотказной работы системы за время t=260 часов:

.

4. Вычисляем среднюю наработку до отказа системы:

, час.

Задача № 4 Для графа состояний восстанавливаемой резервированной системы, изображенного на рис. 3.4 (в соответствии с вариантом: номер варианта определяется двумя последними цифрами номера зачетной книжки студента) необходимо: определить способ структурного резервирования, кратность резервирования, начертить ССН системы, вычислить коэффициент готовности системы К_Г, сделать вывод о необходимости увеличения кратности резервирования системы. Исходные данные для расчета: К_Гзад=0,999; λ=n₁∙10^-4 1/час; μ=n₂∙10^-4 1/час, где n₁ – последняя цифра номера зачетной книжки (цифра 0 соответствует n₁=10); n₂ – предпоследняя цифра номера зачетной книжки (цифра 0 соответствует n₂=10).

Рис. 3.4.

На рис. 3.4 приняты следующие обозначения: G₀ и G₁ – работоспособные состояния системы; G₂ – неработоспособное состояние; Р_i – вероятность нахождения системы в i-ом состоянии; λ – интенсивность отказа; μ – интенсивность восстановления.

Типовой пример. Система обеспечения движения поездов имеет общее резервирование замещением кратности m=1. Интенсивность отказов нерезервированной системы равна λ=0,001 1/ч, а интенсивность восстановления – μ=0,1 1/ч. Необходимо вычислить коэффициент готовности восстанавливаемой резервированной системы К_Г, если заданное значение коэффициента готовности равно К_Гзад = 0,999, а восстановление работоспособного состояния системы является ограниченным.

Решение

1. Чертим структурную схему надежности восстанавливаемой резервированной системы (рис. 3.5)

Рис. 3.5

2. Чертим граф состояний системы (рис. 3.6)

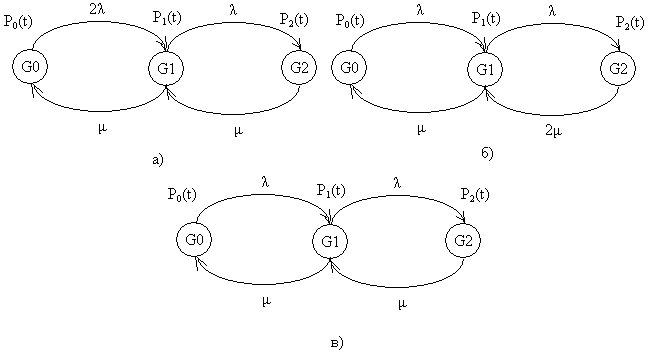
Рис. 3.6

3. С использованием полученного графа состояний системы записываем систему линейных алгебраических уравнений по указанным в разделе 1 правилам (правилам составления дифференциальных уравнений Колмогорова А.Н.):

Полученная система уравнений является линейно зависимой.

4. Приводим данную систему уравнений к системе линейно независимых уравнений путем исключения второго уравнения и добавления нормировочного уравнения:

5. Используя полученную систему уравнений, составляем и вычисляем определители D и D_i (i=0, 1, 2):

P₀ P₁ P₂

P₀ P₁ P₂

P₀ P₁ P₂

P₀ P₁ P₂

6. Вычисляем вероятности нахождения восстанавливаемой резервированной системы в соответствующих состояниях G₀, G₁, G₂:

;

7. Вычисляем коэффициент готовности:

К_Г=P₀(t)+P₁(t)=0,990000+0,009900=0,9999.

Вывод.  Вычисленное значение коэффициента готовности превышает заданное значение ( ). Следовательно, кратность резервирования m=1 является достаточной.

Задача № 4 Для восстанавливающего органа (ВО) типа (в соответствии с вариантом: номер варианта определяется двумя последними цифрами номера зачетной книжки студента) запишите логическую функцию (функцию алгебры логики) и постройте структурную схему на основе логических элементов «И», «ИЛИ». Определите количество отказов по «0» и «1», которое может корректировать восстанавливающий орган данного типа. Исходные данные: и , если или и , если > , где n₁ – последняя цифра номера зачетной книжки (цифра 0 соответствует n₁=10); n₂ – предпоследняя цифра номера зачетной книжки (цифра 0 соответствует n₂=10).

Типовой пример. Для восстанавливающего органа (ВО) типа запишите логическую функцию (функцию алгебры логики) и постройте структурную схему на основе логических элементов «И», «ИЛИ». Определите количество отказов по «0» и «1», которое может корректировать восстанавливающий орган данного типа.

Решение

1. В соответствии с условием: и (так как знак мажоритирования в общем виде записывается как: ).

2. Определяем число корректируемых отказов по «1» ВО типа :

n₁ = ρ – 1 = 2 – 1 = 1.

3. Определяем число корректируемых отказов по «0» ВО типа :

n_о = r – ρ = 3 – 2 = 1.

4. В соответствии с выражением:

запишем логическую функцию (функцию алгебры логики) ВО в дизъюнктивной нормальной форме:

Количество логических слагаемых в данной функции определяется числом сочетаний (в данном случае: ), а количество логических сомножителей в каждом слагаемом определяется значением (в данном случае: ):

5. В соответствии с правилами синтеза комбинационных схем на булевом базисе (логические элементы «И», «ИЛИ», «НЕ») структурная схема ВО типа для полученной логической функции будет иметь вид (рис. 9):

Рис. 3.7