282

2.6. Электромагнитная индукция

2.6.1. Краткие теоретические сведения

1. Работа перемещения проводника с током в магнитном поле ,

где – магнитный поток, пересеченный проводником при его движении.

2. Величина ЭДС индукции в контуре, пронизываемом потоком, определяется

законом Фарадея .

3. ЭДС индукции в проводе длиною , движущемся в магнитном поле со скоростью

равна

если направления и взаимно перпендикулярны.

4. Количество индуцированного электричества в контуре с сопротивлением R при изменении пронизывающего его потока на 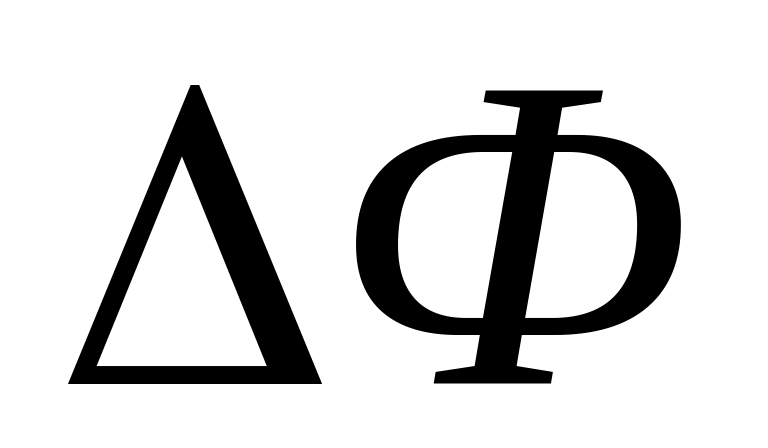равно .

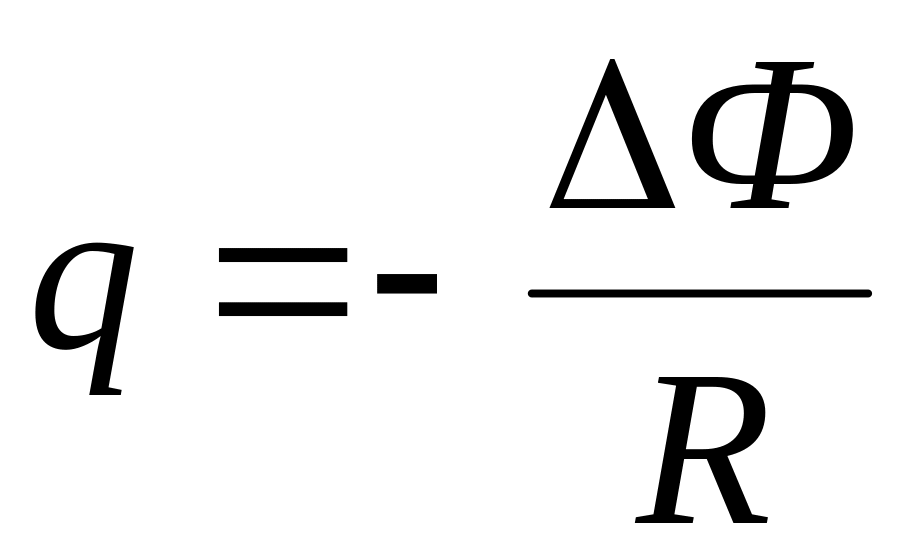5. ЭДС самоиндукции определяется формулой: ,

где L – индуктивность (коэффициент самоиндуктивности контура).

6. Индуктивность контура определяется по формуле: ,

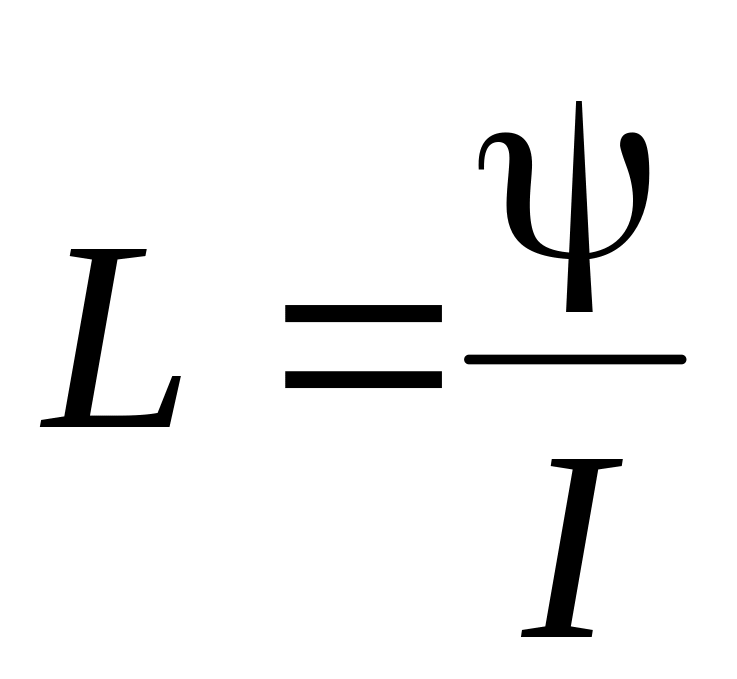где – потокосцепление (полный поток).

7. Индуктивность длинного соленоида равна ,

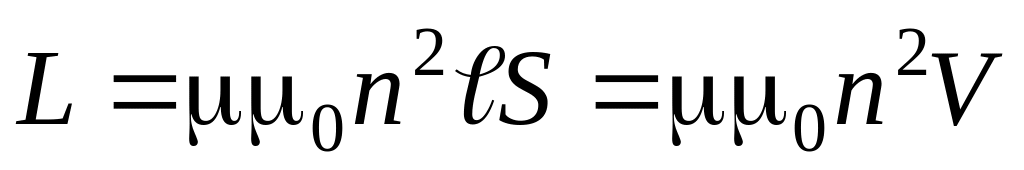где – длина соленоида, S – площадь его поперечного сечения,

– число витков на единицу длины, – объем соленоида.

8. Взаимная индуктивность двух соленоидов, пронизываемых общим магнитным потоком, равна ,

где п₁ и п₂ – число витков на единицу длины этих соленоидов.

9. Мгновенное значение силы тока в цепи, обладающей сопротивлением R и индуктивностью L, определяется формулами:

• при замыкании цепи ,

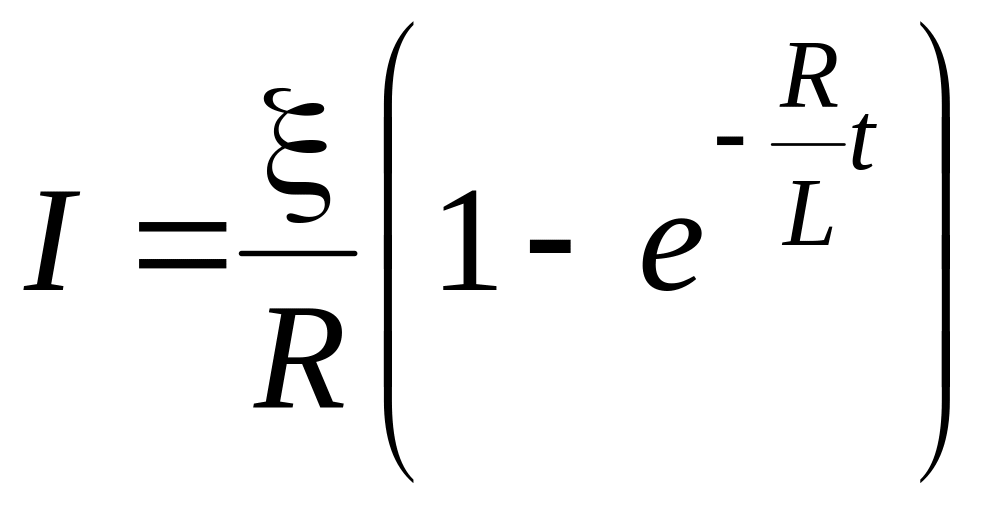где t – время, прошедшее после замыкания цепи;

• при размыкании цепи ,

где – сила тока в цепи в момент времени t = 0, t – время, прошедшее с момента размыкания цепи.

10. Магнитная энергия контура с током (энергия магнитного поля) равна

.

11. Объемная плотность энергии магнитного поля (энергия, заключенная в единице объема):

, или , или .

12. Уравнение Максвелла в интегральной форме

,

,

,

.

2.6.2. Примеры решения задач

ЗАДАЧА 1. Виток, по которому течет ток I = 20 А, свободно установился в однородном магнитном поле с индукцией В = 16 мТл. Диаметр витка d = 10 см. Какую работу нужно совершить, чтобы медленно повернуть виток на угол относительно оси, совпадающей с диаметром?

ДАНО: I = 20 А B = 1610–3 Тл d = 0,1 м

A – ?

АНАЛИЗ. При помещении в магнитное поле витка с током возникает вращающий момент , поворачивающий виток. При этом силы магнитного поля (силы Ампера) совершают работу , где 1 и 2 – начальное и конечное положения контура соответственно.

Работа внешних сил равна .

Поле однородно, , следовательно, для определения магнитного потока Ф необходимо знать угол между нормалью к витку и вектором в начальном и конечном положениях.

РЕШЕНИЕ. В начальном положении (рис. 2.6.1 а) виток находится в состоянии устойчивого равновесия, и момент внешних сил равен нулю , ,

, .

Вектор магнитного момента витка сонаправлен с вектором , и поток Ф₁ максимален

.

В положении 2 (рис. 2.6.1 б) и Ф₂ = 0.

Поэтому

.

Правильность формулы по размерности очевидна.

Подставив значения, получаем: мДж.

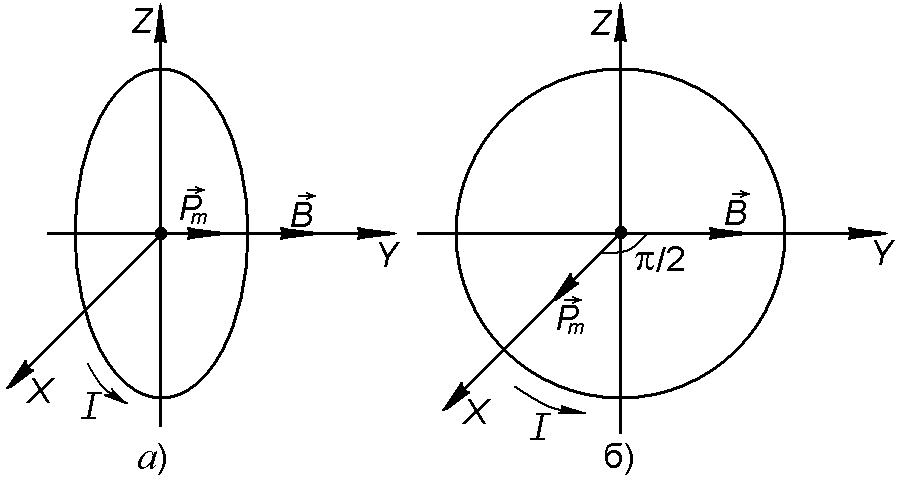
Рис. 2.6.1

ОТВЕТ: мДж.

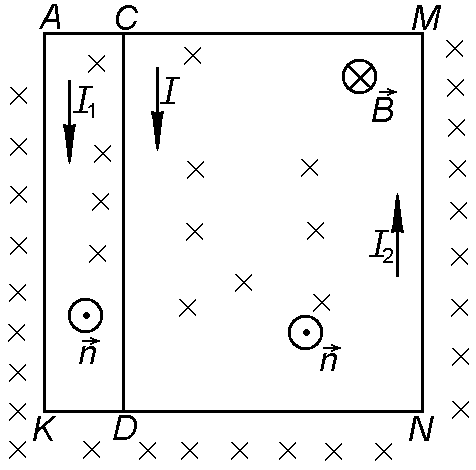
ЗАДАЧА 2. В плоскости, перпендикулярной линиям индукции однородного магнитного поля, расположен проволочный квадрат со стороной а = 4 см. Проволочная перемычка, параллельная двум сторонам квадрата, делит две его другие стороны в отношении 1:3 (рис. 2.6.2). Все проводники выполнены из одинаковой проволоки, для которой отношение сопротивления к длине равно Ом/м. Найти силы токов, индуцируемых во всех проводниках при изменении индукции магнитного поля по линейному закону от В₁ = 510^–3 Тл до В₂ = 8,410^–3 Тл в течение времени с.

ДАНО: a = 0,04 м АС:СМ = 1:3 =1,710–2 Ом/м В1 = 510–3 Тл В2 = 8,410–3 Тл с

I1; I2; I – ?

АНАЛИЗ. При возрастании индукции магнитного поля возникает вихревое электрическое поле, которое вызывает направленное движение свободных электронов, т. е. индукционный ток. Напряженность этого поля связана со скоростью изменения соотношением

, (2.6.1)

Рис. 2.6.2

причем поверхность интегрирования S «натянута» на контур интегрирования , направление обхода образует правовинтовую систему с положительной нормалью к поверхности S. Интеграл в левой части (2.6.1) – это суммарная электродвижущая сила в контуре ; интеграл в правой части – скорость изменения магнитного потока сквозь поверхность S.

Уравнение (2.6.1) позволяет определить ЭДС в контурах ACDKA и CMNDC, и, воспользовавшись законами Кирхгофа, найти токи участков ACDKA – , CMNDC – , СD – I.

РЕШЕНИЕ. При направлении магнитного поля, показанном на рис. 2.6.2, токи и , согласно правилу Ленца, направлены против часовой стрелки. Направление тока в проводнике неизвестно. Выберем это направление, как показано на рис. 2.6.2.

Рассмотрим контур . Магнитное поле однородно и меняется по закону ,

где .

Если положительную нормаль к поверхности контура направить против вектора , то угол между ними и правая часть выражения (2.6.1) имеет вид

.

Тогда ЭДС в контуре .

Для контура аналогично получаем .

По первому правилу Кирхгофа для узла С имеем ,

по второму правилу для контура

,

для контура ,

где ; .

Отсюда .

Проверим размерность:

.

Подставив значения, получаем

. Направление тока соответствует выбранному при решении задачи.

ОТВЕТ:

ЗАДАЧА 3. Две катушки, индуктивности которых мГн, мГн, соединены последовательно (рис. 2.6.3). При этом индуктивность системы мГн. Как изменится индуктивность системы, если в одной из катушек направление тока изменить на противоположное при неизменном взаимном расположении катушек?

ДАНО: L1 = 310–3 Гн L2 = 510–3 Гн L0 = 1110–3 Гн

L0 – ?

АНАЛИЗ. Задача на взаимоиндукцию. Индуктивность системы катушек равна сумме индуктивностей этих катушек и взаимной индуктивности, возникающей при пронизывании данной катушки магнитным потоком (потокосцеплением), создаваемым другими проводниками.

Индуктивность системы определяется потокосцеплением: ;

катушки соединены последовательно, поэтому токи в них одинаковы. Суммарный магнитный поток равен алгебраической сумме потоков, пронизывающих все витки катушки. Все витки первой катушки пронизываются собственным потоком и потоком , созданным второй катушкой. Вторая катушка пронизывается также собственным потоком и потоком , созданным первой катушкой.

Таким образом, .

Собственные потоки положительны и равны соответственно .

а) б)

Рис. 2.6.3

«Чужие» потоки могут быть как положительными, так и отрицательными в зависимости от направления индукции поля, созданного одной катушкой в витках другой. Знаки магнитных потоков и всегда совпадают (при изменении направления тока одновременно изменяются на противоположные и направление положительной нормали, и направление вектора индукции), численные значения их определяются взаимной индуктивностью

.

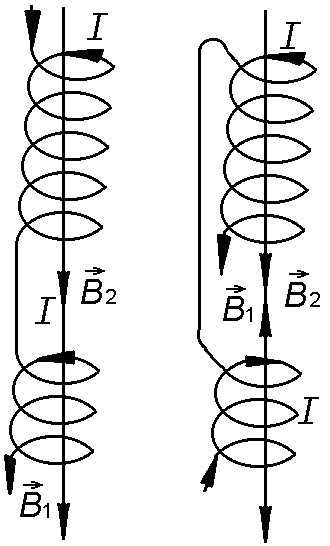
РЕШЕНИЕ. Так как катушки соединены последовательно,

.

Смысл знаков определяется характером соединения и расположения катушек. Если поля катушек сонаправлены и потоки положительны (1 случай), то

.

Во втором случае поля катушек направлены навстречу друг другу, и «чужие» потоки отрицательны

.

Общая индуктивность равна:

• в первом случае ;

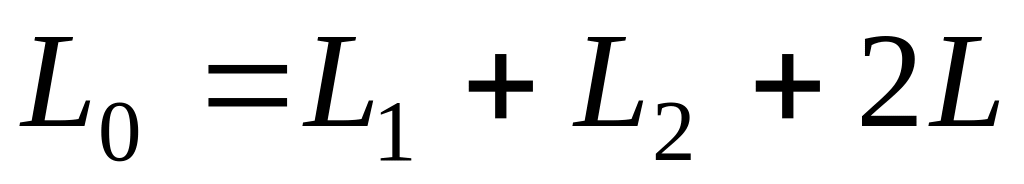• во втором случае ,

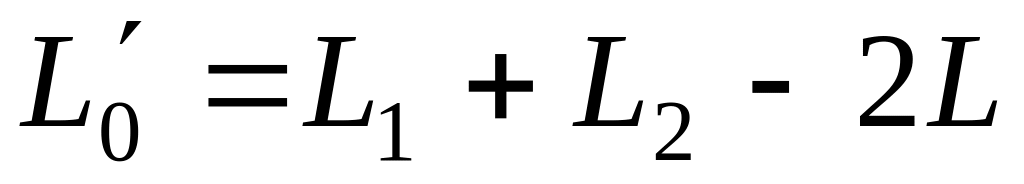Складывая эти выражения, получим

.

Отсюда

.

Правильность формулы по размерности очевидна. Подставив значения, получаем мГн.

ОТВЕТ: мГн.

ЗАДАЧА 4. Телевизионный кабель состоит из двух проводов, один из которых (внутренний) является сплошным цилиндром, а второй (внешний) – полым цилиндром, оси их совпадают. Диаметр первого провода мм, второго – мм. Определить коэффициент самоиндукции, приходящийся на единицу длины этого кабеля.

ДАНО: d1 = 0,310–3 м d2 = 0,810–3 м м

L – ?

АНАЛИЗ. Ток, текущий по кабелю, создает магнитное поле. При изменении тока меняется магнитный поток, пронизывающий кабель, и возникает ЭДС самоиндукции, величина которой определяется коэффициентом самоиндукции.

Для определения коэффициента самоиндукции целесообразно воспользоваться выражениями для энергии магнитного поля.

РЕШЕНИЕ.

Энергия магнитного поля, приходящаяся на единицу длины кабеля , (2.6.2)

где – индуктивность, приходящаяся на единицу длины.

Подставим и объем в формулу для энергии, получаем

. (2.6.3)

Для прямолинейного тока . (2.6.4)

Подставим (2.6.4) в (2.6.3)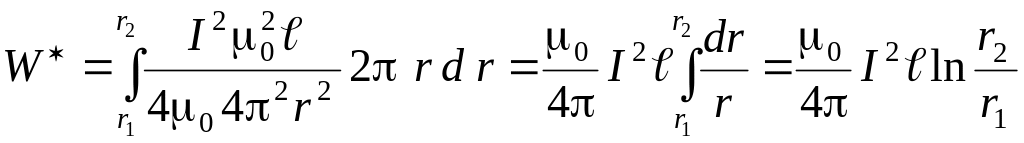 , (2.6.5)

Сравнивая (2.6.3) и (2.6.5), получаем

.

Правильность формулы по размерности очевидна. Подставив значения, получаем Гн/м.

ОТВЕТ: Гн/м.

ЗАДАЧА 5. Длинный проводник радиусом мм согнут пополам так, что расстояние между осями его половинок а = 3 см. Пренебрегая полем внутри проводника, рассчитать индуктивность системы и ее энергию на каждый метр длины при токе А (рис. 2.6.4).

ДАНО: r0 = 210–3 м a = 0,03 м I = 3 А

L – ? – ?

АНАЛИЗ. Индуктивность системы определим по формуле .

Рис. 2.6.4

Чтобы вычислить полный поток системы Ф, надо рассчитать поток, пронизывающий плоскость, ограниченную петлей (поля, созданные каждой частью получившейся петли между проводниками, направлены в одну сторону, за ее пределами – в противоположные).

Магнитный поток равен . (2.6.6)

Индукцию результирующего поля вычислим, считая, что проводник достаточно длинный и можно пренебречь полями токов в подводящих проводах и горизонтальной части проводникаВ = В1+В2,