2.1.3 Задачи для самостоятельной работы Четные – д/з, нечетные – ргр.

1.Два одноименных заряда Q₁=0,7 нКл и Q₂=1,3 нКл находятся в воздухе на расстоянии r=6 см друг от друга. На каком расстоянии между ними нужно поместить третий заряд, чтобы результирующая сила, действующая на каждый заряд, была равна нулю?

2.Три одинаковых заряда q=1 нКл каждый расположены по вершинам равностороннего треугольника. Какой отрицательный заряд q₁ нужно поместить в центре треугольника, чтобы его притяжение уравновесило силы взаимного отталкивания зарядов?

3.Два точечных одинаковых заряда (q=1,1 нКл) находятся на расстоянии r =17 см друг от друга. С какой силой и в каком направлении они действуют на положительный единичный заряд, находящийся на таком же расстоянии от каждого из них?

4. Одноименные заряды Q₁ =0,2 мКл , Q₂ =0,5 мКл и Q₃=0,4 мКл расположены в вершинах треугольника со сторонами а=4 см, b=5 см, с=7 см (рис.2.1.15).Определить модуль и направление силы, действующей на заряд Q₃.

5.В центре квадрата расположен положительный заряд 250 нКл. Какой отрицательный заряд надо поместить в каждой вершине квадрата, чтобы система зарядов находилась в равновесии?

6. В вершинах и в центре правильного треугольника со стороной 5 см расположены положительные одинаковые заряды 0,5 мКл каждый. Какая сила действует на отрицательный заряд 0,7 мКл, находящийся на продолжении высоты, на расстоянии 7 см от вершины?

7 . В вершинах шестиугольника помещены положительные одинаковые заряды 10 нКл каждый. Какой отрицательный заряд надо поместить в центре шестиугольника, чтобы результирующая сила, действующая на каждый заряд, была равна нулю?

8. Шарик массой m = 4 г, несущий заряд нКл, подвешен в воздухе на невесомой нерастяжимой непроводящей нити. При приближении к нему заряда Q₂ противоположного знака нить отклонилась на угол  = 45 от вертикального направления (рис. 2.1.16).Найти модуль заряда Q₂ , если расстояние r = 6 см.

9. В модели атома Бора-Резерфорда электроны движутся по круговым орбитам вокруг положительно заряженного ядра. Определить скорость и ускорение а в атоме водорода, если радиус боровской орбиты r = 52,9 пм.

10. Два шарика массой m = 0,1 г каждый подвешены в одной точке на нитях длиной = 20 см каждая. Получив одинаковый заряд, шарики разошлись так, что нити образовали угол между собой = 60. Найти заряд каждого шарика.

11. Даны два шарика m = 1 г каждый. Какой заряд Q нужно сообщить каждому шарику, чтобы сила взаимного отталкивания зарядов уравновесила силу взаимного притяжения шариков по закону тяготения Ньютона? Рассматривать шарики как материальные точки.

12. Расстояние между двумя точечными зарядами Q₁ = 1 мкКл и Q₂ = –Q₁ равно 10 см. Определите силу F, действующую на точечный заряд мкКл, удаленный на r₁ = 6 см от первого и на r₂ = 8 см от второго зарядов.

13. Два одинаковых проводящих заряженных шара находятся на расстоянии r = 60 см. Сила отталкивания шаров F₁ = 10 мкН. После того, как шары привели в соприкосновение и удалили друг от друга на прежнее расстояние, сила отталкивания возросла и стала равной F₂ = 160 мкН. Вычислить заряды Q₁ и Q₂, которые были на шарах до их соприкосновения. Диаметр шаров считать много меньше расстояния между ними.

14. Два одинаковых проводящих шара находятся на расстоянии см. Сила притяжения шаров F₁ = 90 мкН. После того, как шары были приведены в соприкосновение и удалены друг от друга на прежнее расстояние, сила отталкивания стала равной F₂ = 160 мкН. Вычислить заряды Q₁ и Q₂, которые были на шарах до их соприкосновений. Диаметр шаров считать много меньше расстояния между ними.

15. Два положительных точечных заряда Q и 4Q закреплены на расстоянии = 60 см друг от друга. В какой точке на прямой, проходящей через заряды, следует поместить третий заряд Q₁, чтобы он находился в равновесии. Какой знак должен иметь этот заряд для того, чтобы равновесие было устойчивым, если перемещения заряда возможны только вдоль прямой, проходящей через закреплённые заряды?

16. Расстояние между свободными зарядами Q₁ = 150 нКл и Q₂ = 720 нКл равно 60 см. Определить точку на прямой, проходящей через заряды, в которой нужно поместить третий заряд Q₃ так, чтобы система зарядов находилась в равновесии. Определить величину и знак заряда.

17. Электрическое поле создано двумя точечными зарядами Q₁ = 10 нКл и Q₂ = –20 нКл, находящимися на расстоянии d = 20 см друг от друга. Определить напряженность E поля в точке, удаленной от первого заряда на r₁ = 30 см и от второго на r₂ = 50 см.

18. Расстояние между двумя положительными точечными зарядами Q₁ = 9Q и Q₂ = Q равно d = 8 см. На каком расстоянии r от первого заряда находится точка, в которой напряженность поля зарядов равна нулю? Где находилась бы эта точка, если бы второй заряд был отрицательным?

19. Тонкий стержень длиной = 10 см равномерно заряжен. Линейная плотность заряда τ = 1 мкКл/м. На продолжении оси стержня на расстоянии а = 20 см от ближайшего его конца находится точечный заряд Q = 100 нКл. Определить силу F взаимодействия заряженного стержня и точечного заряда.

20. Тонкий длинный стержень равномерно заряжен с линейной плотностью τ = 10 мкКл/м. На продолжении оси стержня на расстоянии а = 20 см от его конца находится точечный заряд Q = 10 нКл. Определить силу F взаимодействия заряженного стержня и точечного заряда.

21. Тонкий длинный стержень равномерно заряжен с линейной плотностью τ = 10 мкКл/м. Какова сила F, действующая на точечный заряд нКл, находящийся на расстоянии а = 20 см от стержня, против его середины.

22. Тонкая нить длиной = 20 см равномерно заряжена с линейной плотностью τ = 10 нКл/м. На расстоянии а = 10 см от нити против её середины находится точечный заряд q = 1 нКл. Вычислить силу F, действующую на этот заряд со стороны заряженной нити.

23. Тонкое кольцо радиусом R = 10 см несет равномерно распределенный заряд Q = 0,1 мкКл. На перпендикуляре к плоскости кольца, выставленном из его середины, находится точечный заряд Q₁ = 10 нКл. Определить силу F, действующую на точечный заряд Q со стороны заряженного кольца, если он удален от центра кольца на: а) ₁ = 20 см; б) ₂ = 2 м.

24. Тонкое полукольцо радиусом R = 10 см несет равномерно рас­пределенный заряд с линейной плотностью τ = 1 мкКл/м. В центре кривизны полукольца находится заряд Q = 20 нКл. Определить силу F взаимодействия точечного заряда и заряженного полукольца.

25. Тонкое кольцо радиусом R = 8 см несет заряд, равномерно рас­пределенный с линейной плотностью τ = 10 нКл/м. Какова напря­женность Е электрического поля в точке, равноудаленной от всех точек кольца на расстояние r = 10 см?

26. Найти поле объёмно-заряженного шара (объемная плотность за­ряда , радиус – R) для точек, расположенных внутри и вне шара.

27. Очень длинная тонкая прямая проволока несет заряд, равномерно распределенный по всей ее длине. Вычислить линейную плотность заряда, если напряженность Е поля на расстоянии а = 0,5 м от проволоки против ее середины равна 200 В/м.

28. Расстояние d между двумя длинными тонкими проволоками, расположенными параллельно друг другу, равно 16 см. Проволоки равно­мерно заряжены разноименными зарядами с линейной плотностью |τ| =150 мкКл/м. Какова напряженность Е поля в точке, уда­ленной на r = 10 см как от первой, так и от второй проволоки?

29. Две длинные тонкостенные коаксиальные трубки радиусами R₁ = 2 см и R₂ = 4 см несут заряды, равномерно распределенные по длине с линейными плотностями τ₁ = 1 нКл/м и τ₂ = – 0,5 нКл/м. Пространство между трубками заполнено эбонитом. Определить напря­женность Е поля в точках, находящихся на расстоянии r₁ = 1 см, r₂ = 3 см, r₃ = 5 см от оси трубок. Построить график зависимости Е(r).

30. Бесконечно длинная тонкостенная металлическая трубка радиу­сом R = 2 см несет равномерно распределенный по поверхности заряд  = 1 нКл/м. Определить напряженность Е поля в точ­ках, отстоящих от оси трубки на расстояниях r₁ = 1см и r₂ = 3 см. Построить график зависимости Е (r).

31. На металлической сфере радиусом R = 10 см находится заряд нКл. Определить напряженность Е электрического поля в следующих точках: а) на расстоянии r₁ = 8 см от центра сферы; б) на ее поверхности; в) на расстоянии r₂ = 15 см от центра сфе­ры. Построить график зависимости Е от r.

32. Две концентрические металлические заряженные сферы радиусами R₁ = 6 см и R₂ = 10 см несут соответственно заряды Q₁ = 1 нКл и нКл. Найти напряженность E поля в точках, отстоя­щих от центра сфер на расстояниях r₁ = 5 см, r₂ = 9 см, r₃ = 15 см. Построить график зависимости Е(r).

33. Найти потенциал и напряженность поля Е в центре сферы радиусом R, заряженной однородно с поверхностной плотностью .

34. Заряд q = 2 мКл распределен равномерно по объему шара радиусом R = 40 мм. Найти потенциал  и напряженность поля Е в центре шара.

35. Определить напряженность электрического поля, потенциал кото­рого зависит от координат x и y по закону: а) ; б) , где а – постоянная. Изобразить примерный вид этих полей с помощью линий вектора (в плоскости XY).

36. Найти потенциалы следующих электростатических полей: а) ; б) , здесь a – посто­янная, а и – орты координатных осей.

37. Электрическое поле создано двумя бесконечными параллельными пластинами, несущими одинаковый равномерно распределенный по площа­ди заряд  = 1 нКл/м² . Определить напряженность поля Е: а) между пластинами; б) вне пластин. Построить график изменения напряженности вдоль линии, перпендикулярной пластинам.

38. По тонкому кольцу радиусом R = 10 см равномерно распределен заряд с линейной плотностью τ = 10 нКл/м. Определить потенциал в точке, лежащей на оси кольца на расстоянии а = 5 см от центра.

39. Напряженность некоторого электростатического поля определяется выражением , где а – константа. Является ли это поле однородным? Найдите потенциал этого поля.

40. Бесконечно тонкая прямая нить несет равномерно распределенный по её длине заряд с плотностью нКл/м. Каков градиент по­тенциала в точке, удаленной на расстояние r = 10 см от нити? Указать направление градиента потенциала.

41. Потенциал поля, создаваемого некоторой системой зарядов, имеет вид: , где а и b – константы. а) Найти напряженность поля и ее модуль E; б) какую форму имеют эквипотенциальные поверхности; в) какую форму имеют поверхности, для которых = ?

42. Заряд распределен равномерно по бесконечной плоскости с повер­хностной плотностью  = 10 нКл/м². Определить разность потенци­алов ∆ двух точек поля, одна из которых находится на плоскости, а другая удалена от плоскости на расстояние d = 10 см.

Рис. 2.1.17

Рис. 2.1.18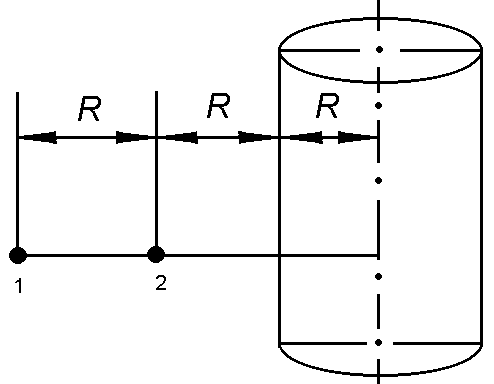

43. Две бесконечные параллельные плоскости находятся на расстоянии d = 0,5 см друг от друга. На плоскостях равномерно распре­делены заряды с поверхностными плотностями ₁ = 0,2 мкКл/м² и ₂ = – 0,3 мкКл/м². Определить разность потенциалов ∆ между плоскостями.

44. Электрическое поле создано бесконечно длинным равномерно заря­женным ( = 0,1 мкКл/м²) цилиндром радиусом R = 5 см. Опреде­лить изменение потенциальной энергии ∆W_n положительного однозарядного иона при перемещении его из точки 1 в точку 2 (рис. 2.1.17).

45. Электрический диполь состоит из двух зарядов +q и –q по 10^–7 Кл каждый. Расстояние между зарядами 2 см (рис. 2.1.18). Вычислить полный поток, выходящий из сферической поверхности радиусом 2 см, центр которой совпадает с центром диполя. Какой электрический по­тенциал в центре сферы? Чему равна величина напряженности электри­ческого поля в центре сферы?

46. Бесконечная плоскость несет заряд, равномерно распределенный с поверхностной плотностью  = 1 мкКл/м². На некотором расстоя­нии от плоскости параллельно ей расположен круг радиусом r = 10 см. Вычислить поток N_Е вектора напряженности через этот круг.

47. В центре сферы радиусом R = 20 см находится точечный заряд нКл. Определить поток N_Е вектора напряженности через часть сферической поверхности площадью S = 20 см².

48. Прямоугольная плоская площадка со сторонами а = 3 см и b = 2 см находится на расстоянии R = 1 м от точечного заряда Q = 1 мкКл. Площадка ориентирована так, что линии напряженности составляют угол = 30 с ее поверхностью. Найти поток N_Е век­тора напряженности через площадку.

49. Потенциал поля в некоторой области пространства зависит только от координаты х: = – ax³+b, где а и b – постоянные. Найти распределение объемного заряда.

50. Найти зависимость плотности зарядов ρ от декартовых коорди­нат x, y, z, при которой напряженность поля описывалась бы функцией .

51. Найти зависимость плотности зарядов ρ от модуля r радиуса-вектора, при которой напряженность поля описывалась бы функцией , где А и а – константы.

52. Может ли электростатическое поле иметь напряженность ?

53. Диполь с электрическим моментом p = 1 пКлм равномерно враща­ется с частотой n = 10^–3 с^–1 относительно оси, проходящей через центр диполя и перпендикулярной его плечу. Вывести закон изменения потенциала как функцию времени в некоторой точке, отстоящей от центра диполя на r = 1 см и лежащей в плоскости вращения диполя. Принять, что в начальный момент времени потенциал φ₀ интересую­щей Вас точки равен нулю. Построить график зависимости φ(t).

54. Два диполя с электрическими моментами p₁ = 1 пКлм и p₂ = 4 пКлм находятся на расстоянии r = 2 см друг от друга. Найти силу их взаимодействия, если оси диполей лежат на одной пря­мой.

55. Два диполя с электрическими моментами р₁ = 20 пКлм и пКлм находятся на расстоянии r = 10 см друг от друга так, что их оси лежат на одной прямой. Вычислить взаимную потенциальную энергию диполей, соответствующую их устойчивому равновесию.

56. Диполь с электрическим моментом пКлм свободно уста­навливается в однородном электрическом поле напряженностью . Вычислить работу A, необходимую для того, чтобы повернуть диполь на угол = 180.