Основное уравнение молекулярно-кинетической теории газов.

Систему характеризуют макро и микропараметры.

К макропараметрам относятся давление, объем, температура, эти параметры мы можем измерить приборами.

К микропараметрам относятся скорость, масса и концентрация молекул: v, m₀ , n.

Основное уравнение молекулярно-кинетической теории связывает макро и микропараметры газа.

 

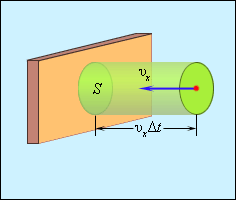
Если молекула летит под углом к стенке, то, как следует из рисунка, изменение проекции импульса на ось x есть p_x = 2m₀v_x, изменение проекции импульса на ось y есть p_y = 0. Следовательно,

f_x    0, f_y   = 0, т.е. в результате удара независимо от того, как летит молекула, на стенку действует сила, направленная перпендикулярно стенке.

Вывод основного уравнения молекулярно-кинетической теории.

Сделаем ряд вспомогательных предположений.

1) Газ идеальный.

2) Молекулы можно разделить на группы. Пусть N₁ молекул имеют скорость v₁, N₂ – скорость v₂, …, N_n – скорость v_n. Концентрация молекул первой группы n₁ = , второй – n₂ = , …, n_n = , где V – объем сосуда. Очевидно, что N₁ + N₂ + … + N_n = N, где N – общее число молекул, n₁ + n₂ + … + n_n, где n – концентрация молекул в сосуде. Это предположение, строго говоря, неверно, так как в силу непрерывного хаотического движения число молекул, имеющих данную скорость, может непрерывно изменяться. Можно указать число молекул, скорости которых изменяются в некотором интервале скоростей. Например, N₁ молекул, скорости которых изменяются от v₁ до v₁ + v, N₂ молекул, скорости которых изменяются в пределах от v₂ до v₂ + v и т.д. Однако при выводе основного уравнения молекулярно-кинетической теории некорректность этого предположения не играет существенной роли.

3) Направления движения молекул равновероятны. Пусть молекулы движутся по трем взаимно-перпендикулярным направлениям. В среднем в каждом направлении движется частиц.

Рассмотрим молекулы i-ой группы, движущиеся вдоль оси x. В результате удара о стенку одной молекулы этой группы на стенку действует импульс силы:

f_ст.i   = 2m₀v_i.

За некоторый промежуток времени t о стенку площадью S ударится не одна молекула, а z_i молекул:

z_i = ,

т.е. все молекулы, движущиеся по направлению к стенке (т.е. ) и находящиеся в объеме Sv_it .

Итак, средний импульс силы, подействовавший на стенку в результате удара о нее молекул i-ой группы, за время t равен:

F_it = n_iSm₀ t.

Давление равно р = , отсюда давление на стенку, оказываемое молекулами i-ой группы, есть

р_i = = .

На стенку налетают молекулы всех групп, следовательно, суммарное давление равно

р = .

Введем понятие средне-квадратичной скорости:

= .

Разделим числитель и знаменатель на объем сосуда:

= = ,

откуда

р = nm₀ .

Средняя кинетическая энергия молекулы равна:

= ,

таким образом,

р = n – основное уравнение молекулярно-кинетической теории. Давление газа пропорционально концентрации молекул и средней кинетической энергии поступательного движения молекулы.

Из уравнения Клапейрона-Менделеева следует:

р = nkT.

Приравняв выражения (8.20) и (8.21), получим для :

= kT.

Абсолютная температура – мера кинетической энергии поступательного движения молекул. Если T  0, то  0. Абсолютный нуль температуры – это температура, при которой прекращается поступательное движение молекул.

v_ср.кв = .