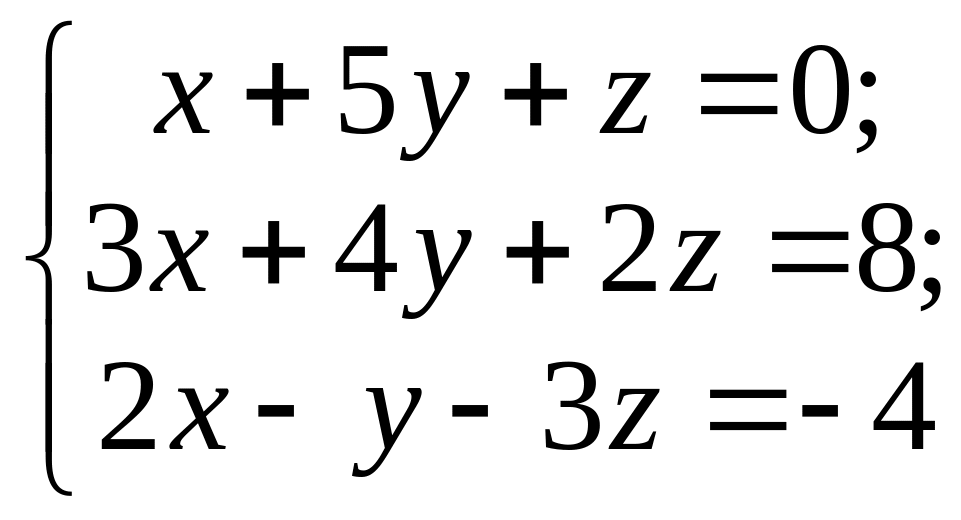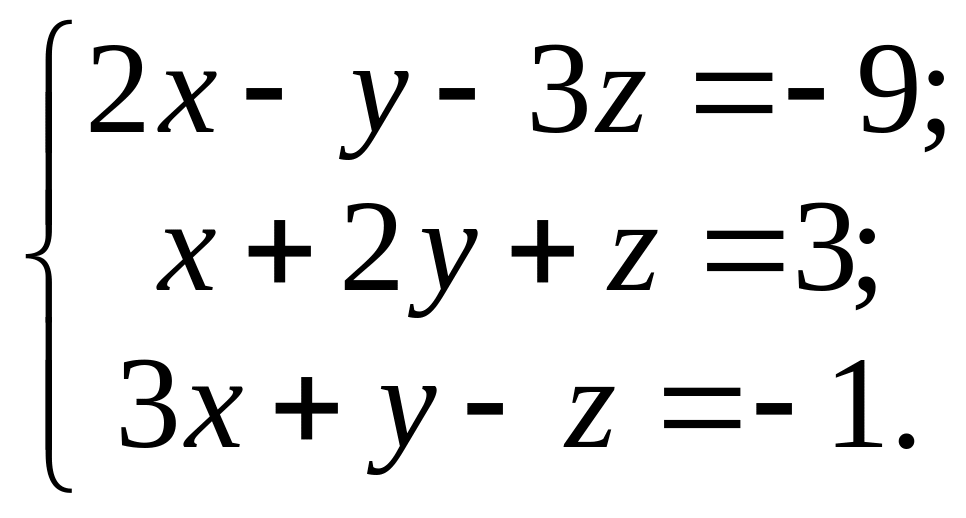Міністерство освіти і науки України
ОДЕСЬКИЙ НАЦІОНАЛЬНИЙ ПОЛІТЕХНІЧНИЙ УНІВЕРСИТЕТ
ІНДИВІДУАЛЬНІ ДОМАШНІ ЗАВДАННЯ
З ВИЩОЇ МАТЕМАТИКИ
І МЕТОДИЧНІ ВКАЗІВКИ ДО ЇХНЬОГО ВИКОНАННЯ
для студентів 1 курсу спеціальності РК
І семестр
Одеса ОНПУ 2008
Міністерство освіти і науки України
Одеський національний політехнічний університет
Індивідуальні домашні завдання
з вищої математики
і методичні вказівки до їхнього виконання
для студентів 1 курсу спеціальності РК
І семестр
Затверджено
на засіданні кафедри
вищої математики і
моделювання систем
Протокол № 2 від 10. 01. 08
Одеса ОНПУ 2008
Індивідуальні домашні завдання з вищої математики і методичні вказівки до їхнього виконання для студентів 1 курсу спеціальності РК денної форми навчання і семестру / Укл.: В.М. Кузьміна, Т.М. Олех. – Одеса: ОНПУ, 2008. – 61 c.
Укладачі: В.М. Кузьміна,
Т.М. Олех,
старші викладачі
Вступ
У першому семестрі курс вищої математики складається з двох модулів. Кожен модуль складається з аудиторних занять та індивідуальної роботи студентів. Обсяг і зміст семестрових індивідуальних завдань визначається робочою програмою курсу. Кожен модульний контроль оцінюється виходячи з 50 балів. Розподіл балів в межах кожного модульного контролю виконується залежно від обсягу навчальних складових дисципліни згідно з робочою навчальною програмою. Модульний контроль складається з поточного контролю та модульної контрольної роботи. Модульна контрольна робота виконується у письмовій формі з використанням тестових технологій. Сума балів одержана за виконання індивідуального домашнього завдання зараховується у поточний контроль.
При виконанні й оформленні індивідуальних домашніх завдань студент повинен дотримуватися таких правил:
а) виконувати завдання в окремому зошиті у клітинку 12 або 18 аркушів;
б) вказати на обкладинці прізвище та ініціали, номер групи та номер варіанта;
в) розв’язання задач розташовувати в довільному порядку, зазначаючи їх номери, виписуючи перед розв’язанням кожної задачі її умову;
г) у разі необхідності розв’язання задач супроводжувати кресленнями, креслення виконувати олівцем.
Кожна задача індивідуальних домашніх завдань складається з 30 варіантів. Студент виконує варіант, номер якого визначається викладачем або за своїм номером у списку групи.
Програма дисципліни «Вища математика» у першому семестрі передбачає вивчення лінійної алгебри, векторної алгебри та аналітичної геометрії, комплексних чисел та вступу у математичний аналіз.
Список літератури
Пак В.В., Носенко Ю.Л. Вища математика. – К.: Либідь, 1996.
Вища математика: основні розділи: Підруч.: У 2 кн. /За ред. Кулініча Г.Л. – К.:Либідь, 1997.
Кліх Ю.О., Плотнікова Л.І., Усов А.В. Лінійна алгебра та елементи аналітичної геометрії. Одеса, – ОДПУ, 1998.
Вища математика: основні означення, приклади і задачі: У 2 кн. /За ред. Васильченка І.П. – К.:Либідь, 1992.
Кривуца В.Г., Барковський В.В., Барковська Н.В. Вища математика. Практикум: Навчальний посібник.- Київ: Центр навчальної літератури, 2005.
Берман Г.Н., Сборник задач по курсу математического анализа.- М.: Наука,-1972.
Кузнецов Л.А. Сборник заданий по высшей математике. (Типовые расчеты). - М.: Высшая школа, 1983.
Задача 1. Виконати дії. Представити результат в алгебраїчній формі.
1 |
|
11 |
|
21 |
|
2 |
|
12 |
|
22 |
|
3 |
|
13 |
|
23 |
|
4 |
|
14 |
|
24 |
|
5 |
|
15 |
|
25 |
|
6 |
|
16 |
|
26 |
|
7 |
|
17 |
|
27 |
|
8 |
|
18 |
|
28 |
|
9 |
|
19 |
|
29 |
|
10 |
|
20 |
|
30 |
|
Задача 2. Виконати дії. Представити результат у показниковій формі.
1 |
|
11 |
|
21 |
|
2 |
|
12 |
|
22 |
|
3 |
|
13 |
|
23 |
|
4 |
|
14 |
|
24 |
|
5 |
|
15 |
|
25 |
|
6 |
|
16 |
|
26 |
|
7 |
|
17 |
|
27 |
|
8 |
|
18 |
|
28 |
|
9 |
|
19 |
|
29 |
|
10 |
|
20 |
|
30 |
|
Задача 3.
Обчислити значення
та побудувати їх на площині комплексної
змінної.
1 |
|
11 |
|
21 |
|
2 |
|
12 |
|
22 |
|
3 |
|
13 |
|
23 |
|
4 |
|
14 |
|
24 |
|
5 |
|
15 |
|
25 |
|
6 |
|
16 |
|
26 |
|
7 |
|
17 |
|
27 |
|
8 |
|
18 |
|
28 |
|
9 |
|
19 |
|
29 |
|
10 |
|
20 |
|
30 |
|
Задача 4. Побудувати на площині комплексної змінної множину точок, що задовольняють заданим умовам.
1 |
|
11 |
|
21 |
|
2 |
|
12 |
|
22 |
|
3 |
|
13 |
|
23 |
|
4 |
|
14 |
|
24 |
|
5 |
|
15 |
|
25 |
|
6 |
|
16 |
|
26 |
|
7 |
|
17 |
|
27 |
|
8 |
|
18 |
|
28 |
|
9 |
|
19 |
|
29 |
|
10 |
|
20 |
|
30 |
|
Задача 5. Розв'язати систему лінійних неоднорідних алгебраїчних рівнянь: 1) за правилом Крамера; 2) методом Жордана – Гауса; 3) за допомогою оберненої матриці.
1 |
|
11 |
|
21 |
|
2 |
|
12 |
|
22 |
|
3 |
|
13 |
|
23 |
|
4 |
|
14 |
|
24 |
|
5 |
|
15 |
|
25 |
|
6 |
|
16 |
|
26 |
|
7 |
|
17 |
|
27 |
|
8 |
|
18 |
|
28 |
|
9 |
|
19 |
|
29 |
|
10 |
|
20 |
|
30 |
|
Задача 6. Дана система лінійних однорідних алгебраїчних рівнянь. Знайти фундаментальну систему розв'язків та загальний розв'язок системи.
1 |
|
16 |
|
2 |
|
17 |
|
3 |
|
18 |
|
4 |
|
19 |
|
5 |
|
20 |
|
6 |
|
21 |
|
7 |
|
22 |
|
8 |
|
23 |
|
9 |
|
24 |
|
10 |
|
25 |
|
11 |
|
26 |
|
12 |
|
27 |
|
13 |
|
28 |
|
14 |
|
29 |
|
15 |
|
30 |
|
Задача 7. Написати розкладання вектора X по векторах P, Q, R.
1 |
X=(-1,0,2) |
P=(1,-1,0) |
Q=(1,2,0) |
R=(1,-4,2) |
2 |
X=(4,4,-6) |
P=(1,1,0) |
Q=(0,-1,2) |
R=(2,-1,0) |
3 |
X=(8,3,2) |
P=(4,1,1) |
Q=(1,1,-1) |
R=(2,0,3) |
4 |
X=(1,0,2) |
P=(-2,2,0) |
Q=(-5,2,-2) |
R=(-3,2,2) |
5 |
X=(0,1,2) |
P=(1,0,4) |
Q=(-2,1,7) |
R=(1,0,2) |
6 |
X=(-2,4,7) |
P=(0,1,2) |
Q=(1,0,1) |
R=(-1,2,4) |
7 |
X=(6,12,-1) |
P=(1,3,0) |
Q=(2,-1,1) |
R=(0,-1,2) |
8 |
X=(1,-4,4) |
P=(2,1,-1) |
Q=(0,3,2) |
R=(1,-1,1) |
9 |
X=(-9,5,5) |
P=(1,1,1) |
Q=(2,0,-3) |
R=(-1,2,1) |
10 |
X=(-5,-5,5) |
P=(-2,0,1) |
Q=(1,3,-1) |
R=(0,4,1) |
11 |
X=(13,2,7) |
P=(5,1,0) |
Q=(2,-1,3) |
R=(1,0,-1) |
12 |
X=(-19,-1,7) |
P=(0,1,1) |
Q=(-2,0,1) |
R=(3,1,0) |
13 |
X=(3,-1,4) |
P=(1,0,2) |
Q=(0,1,1) |
R=(2,-1,4) |
14 |
X=(3,3.-1) |
P=(3,1,0) |
Q=(-1,2,1) |
R=(-1,0,2) |
15 |
X=(-1,7,-4) |
P=(-1,2,1) |
Q=(2,0,3) |
R=(1,1,-1) |
16 |
X=(6,5,-14) |
P=(1,1,4) |
Q=(0,-3,2) |
R=(2,1,-1) |
17 |
X=(6,-1,7) |
P=(1,-2,0) |
Q=(-1,1,3) |
R=(1,0,4) |
18 |
X=(5,15,0) |
P=(1,0,5) |
Q=(-1,3,2) |
R=(0,-1,1) |
19 |
X=(2,-1,11) |
P=(1,1,0) |
Q=(0,1,-2) |
R=(1,0,3) |
20 |
X=(11,5,-3) |
P=(1,0,2) |
Q=(-1,0,1) |
R=(2,5,-3) |
21 |
X=(8,0,5) |
P=(2,0,1) |
Q=(1,1,0) |
R=(4,1,2) |
22 |
X=(3,1,8) |
P=(0,1,3) |
Q=(1,2,-1) |
R=(2,0,-1) |
23 |
X=(8,1,12) |
P=(1,2,-1) |
Q=(3,0,2) |
R=(-1,1,1) |
24 |
X=(-9,-8,-3) |
P=(1,4,1) |
Q=(-3,2,0) |
R=(1,-1,2) |
25 |
X=(-5,9,-13) |
P=(0,1,-2) |
Q=(3,-1,1) |
R=(4,1,0) |
26 |
X=(-15,5,6) |
P=(0,1,5) |
Q=(3,2,-1) |
R=(-1,1,0) |
27 |
X=(8,9,4) |
P=(1,0,1) |
Q=(0,-2,1) |
R=(1,3,0) |
28 |
X=(23,-14,-30) |
P=(2,1,0) |
Q=(1,-1,0) |
R=(-3,2,5) |
29 |
X=(3,1,3) |
P=(2,1,0) |
Q=(1,0,1) |
R=(4,2,1) |
30 |
X=(-1,7,0) |
P=(0,3,1) |
Q=(1,-1,2) |
R=(2,-1,0) |
Задача
8. Задані координати точок А, В
та С. Знайти кут між векторами
та
.
1 |
А(1,-2,3), В(0,-1,2), С(3,-4,5) |
16 |
А(3,-6,9), В(0,-3,6), С(9,-12,15) |
2 |
А(0,-3,6), В(-12,-3,-3), С(-9,-3,-6) |
17 |
А(0,2,-4), В(8,2,2), С(6,2,4) |
3 |
А(3,3,-1), В(5,5,-2), С(4,1,1) |
18 |
А(3,3,-1), В(5,1,-2), С(4,1,1) |
4 |
А(-1,2,-3), В(3,4,-6), С(1,1,-1) |
19 |
А(-4,3,0), В(0,1,3), С(-2,4,-2) |
5 |
А(-4,-2,0), В(-1,-2,4), С(3,-2,1) |
20 |
А(1,-1,0), В(-2,-1,4), С(8,-1,-1) |
6 |
А(5,3,-1), В(5,2,0), С(6,4,-1) |
21 |
А(7,0,2), В(7,1,3), С(8,-1,2) |
7 |
А(-3,-7,-5), В(0,-1,-2), С(2,3,0) |
22 |
А(2,3,2), В(-1,-3,-1), С(-3,-7,-3) |
8 |
А(2,-4,6), В(0,-2,4), С(6,-8,10) |
23 |
А(2,2,7), В(0,0,6), С(-2,5,7) |
9 |
А(0,1,-2), В(3,1,2), С(4,1,1) |
24 |
А(-1,2,-3), В(0,1,-2), С(-3,4,-5) |
10 |
А(3,3,-1), В(1,5,-2), С(4,1,1) |
25 |
А(0,3,-6), В(9,3,6), С(12,3,3) |
11 |
А(2,1,-1), В(6,-1,-4), С(4,2,1) |
26 |
А(3,3,-1), В(5,1,-2), С(4,1,-3) |
12 |
А(-1,-2,1), В(-4,-2,5), С(-8,-2,2) |
27 |
А(-2,1,1), В(2,3,-2), С(0,0,3) |
13 |
А(6,2,-3), В(6,3,-2), С(7,3,-3) |
28 |
А(1,4,-1), В(-2,4,-5), С(8,4,0) |
14 |
А(0,0,4), В(-3,-6,1), С(-5,-10,-1) |
29 |
А(0,1,0), В(0,2,1), С(1,2,0) |
15 |
А(2,-8,-1), В(4,-6,0), С(-2,-5,-1) |
30 |
А(-4,0,4), В(-1,6,7), С(1,10,9) |
Задача
9. Обчислити площу паралелограма,
побудованого на векторах
та
.
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
10 |
|
11 |
|
12 |
|
13 |
|
14 |
|
15 |
|
16 |
|
17 |
|
18 |
|
19 |
|
20 |
|
21 |
|
22 |
|
23 |
|
24 |
|
25 |
|
26 |
|
27 |
|
28 |
|
29 |
|
30 |
|
Задача
10. Обчислити об’єм трикутної піраміди
з вершинами
та її висоту, проведену з вершини
на грань
.
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
10 |
|
11 |
|
12 |
|
13 |
|
14 |
|
15 |
|
16 |
|
17 |
|
18 |
|
19 |
|
20 |
|
21 |
|
22 |
|
23 |
|
24 |
|
25 |
|
26 |
|
27 |
|
28 |
|
29 |
|
30 |
|
Задача 11. Задані координати точок A і B. Скласти рівняння прямої АВ та рівняння перпендикулярної до AB прямої, що проходить через середину відрізку АВ.
1 |
A(-4,1) |
B(12,13) |
11 |
A(-3,2) |
B(9,2) |
21 |
A(-6,8) |
B(18,4) |
2 |
A(-4,1) |
B(8,17) |
12 |
A(-3,2) |
B(13,10) |
22 |
A(-7,5) |
B(25,13) |
3 |
A(-4,2) |
B(12,14) |
13 |
A(-12,3) |
B(42,9) |
23 |
A(-5,4) |
B(23,20) |
4 |
A(-4,2) |
B(8,18) |
14 |
A(-1,4) |
B(11,0) |
24 |
A(-2,4) |
B(18,24) |
5 |
A(-4,4) |
B(12,16) |
15 |
A(-1,4) |
B(15,4) |
25 |
A(-9,8) |
B(33,16) |
6 |
A(-4,4) |
B(8,20) |
16 |
A(-8,4) |
B(16,22) |
26 |
A(-5,4) |
B(35,36) |
7 |
A(-6,3) |
B(10,15) |
17 |
A(-7,3) |
B(25,3) |
27 |
A(-6,8) |
B(18,32) |
8 |
A(-8,4) |
B(4,20) |
18 |
A(-1,4) |
B(11,4) |
28 |
A(-8,7) |
B(28,21) |
9 |
A(-6,6) |
B(10,18) |
19 |
A(-5,2) |
B(27,14) |
29 |
A(-3,8) |
B(21,4) |
10 |
A(-8,8) |
B(4,24) |
20 |
A(-7,4) |
B(37,12) |
30 |
A(-7,9) |
B(17,3) |
Задача 12. Задані координати точок A,B,C,D. Скласти рівняння площини ABC і знайти відстань від точки D до цієї площини. Знайти точку D' симетричну точці D відносно площини ABC.
1 |
A(1,3,6) |
B(2,2,1) |
C(-1,0,1) |
D(-4,6,-3) |
2 |
A(-2,2,8) |
B(2,4,6) |
C(-1,5,8) |
D(3,-3,-2) |
3 |
A(7,2,-4) |
B(7,-1,2) |
C(6,3,-7) |
D(3,-8,-6) |
4 |
A(2,1,4) |
B(-1,5,-2) |
C(-7,-3,2) |
D(-3,3,6) |
5 |
A(-1,-5,2) |
B(-6,0,-3) |
C(3,6,-3) |
D(-10,6,7) |
6 |
A(0,-1,-1) |
B(3,-2,3) |
C(0,2,-7) |
D(-30,10,6) |
7 |
A(5,2,0) |
B(2,5,0) |
C(1,2,4) |
D(-1,1,1) |
8 |
A(2,-1,-2) |
B(1,2,1) |
C(5,0,-6) |
D(-10,9,-7) |
9 |
A(-2,0,-4) |
B(-1,7,1) |
C(4,-8,-4) |
D(1,-4,6) |
10 |
A(1,3,0) |
B(4,-1,2) |
C(3,0,1) |
D(4,3,0) |
11 |
A(-2,3,-5) |
B(4,0,-3) |
C(-3,4,-6) |
D(1,1,1) |
12 |
A(2,-1,2) |
B(1,2,-1) |
C(3,2,1) |
D(-4,2,5) |
13 |
A(1,1,2) |
B(-1,1,3) |
C(2,-2,4) |
D(-1,0,-2) |
14 |
A(2,3,1) |
B(4,1,-2) |
C(6,3,7) |
D(7,5,-3) |
15 |
A(1,1,-1) |
B(2,3,1) |
C(3,2,1) |
D(5,12,-8) |
16 |
A(1,5,-7) |
B(-3,6,3) |
C(-2,7,3) |
D(-4,8,-12) |
17 |
A(-4,2,6) |
B(2,-3,0) |
C(-10,5,8) |
D(-9,-5,5) |
18 |
A(-1,2,-3) |
B(4,-1,0) |
C(2,1,-2) |
D(3,4,5) |
19 |
A(4,-1,3) |
B(-2,1,0) |
C(0,-5,1) |
D(3,2,-6) |
20 |
A(2,-3,1) |
B(4,-1,5) |
C(7,2,-1) |
D(1,2,3) |
21 |
A(1,2,0) |
B(1,-1,2) |
C(0,1,-1) |
D(-3,0,1) |
22 |
A(1,0,2) |
B(1,2,-1) |
C(2,-2,1) |
D(2,1,0) |
23 |
A(1,2,-3) |
B(1,0,1) |
C(-2,-1,6) |
D(-2,-5,-4) |
24 |
A(3,10,-1) |
B(-2,3,-5) |
C(-6,0,-3) |
D(1,-1,2) |
25 |
A(-1,2,4) |
B(-1,-2,-4) |
C(-3,0,-1) |
D(0,6,2) |
26 |
A(0,-3,1) |
B(-4,1,2) |
C(2,-1,5) |
D(3,1,-4) |
27 |
A(1,3,0) |
B(4,-1,2) |
C(3,0,1) |
D(-4,3,5) |
28 |
A(-2,-1,-1) |
B(0,3,-40) |
C(4,1,-4) |
D(8,9,19) |
29 |
A(-3,-5,6) |
B(3,1,-4) |
C(0,-3,0) |
D(-7,20,-13) |
30 |
A(2,-4,-3) |
B(5,-6,0) |
C(-1,3,-3) |
D(-10,-8,11) |
Задача 13. Задані координати точки A та рівняння двох площин Р1 і Р2. Знайти кут між площинами. Скласти канонічне рівняння їх лінії перетину.
№ |
А |
Р1 |
Р2 |
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
|
6 |
|
|
|
7 |
|
|
|
8 |
|
|
|
9 |
|
|
|
10 |
|
|
|
11 |
|
|
|
12 |
|
|
|
13 |
|
|
|
14 |
|
|
|
15 |
|
|
|
16 |
|
|
|
17 |
|
|
|
18 |
|
|
|
19 |
|
|
|
20 |
|
|
|
21 |
|
|
|
22 |
|
|
|
23 |
|
|
|
24 |
|
|
|
25 |
|
|
|
26 |
|
|
|
27 |
|
|
|
28 |
|
|
|
29 |
|
|
|
30 |
|
|
|
Задача 14. Лінія задана рівнянням у полярній системі координат. Визначити рівняння кривої у прямокутній декартовій системі координат, в якої початок координат збігається з полюсом, а невід'ємна піввісь абсцис – з поляр-ною віссю. Звести це рівняння до канонічного вигляду і визначити тип кривої.
1 |
|
11 |
|
21 |
|
2 |
|
12 |
|
22 |
|
3 |
|
13 |
|
23 |
|
4 |
|
14 |
|
24 |
|
5 |
|
15 |
|
25 |
|
6 |
|
16 |
|
26 |
|
7 |
|
17 |
|
27 |
|
8 |
|
18 |
|
28 |
|
9 |
|
19 |
|
29 |
|
10 |
|
20 |
|
30 |
|
Задача 15. Знайти власні вектори та власні значення матриці.
1 |
|
11 |
|
21 |
|
2 |
|
12 |
|
22 |
|
3 |
|
13 |
|
23 |
|
4 |
|
14 |
|
24 |
|
5 |
|
15 |
|
25 |
|
6 |
|
16 |
|
26 |
|
7 |
|
17 |
|
27 |
|
8 |
|
18 |
|
28 |
|
9 |
|
19 |
|
29 |
|
10 |
|
20 |
|
30 |
|
Задача 16. Дослідити на знаковизначеність квадратичну форму
.
та звести її до канонічного вигляду методом ортогональних перетворень.
|
а |
b |
с |
k |
n |
p |
|
а |
b |
с |
k |
n |
p |
1 |
1 |
1 |
-7 |
1 |
-2 |
2 |
16 |
1 |
-7 |
1 |
-2 |
-2 |
2 |
2 |
2 |
1 |
1 |
-2 |
2 |
-3 |
17 |
1 |
1 |
5 |
-3 |
1 |
-1 |
3 |
11 |
5 |
2 |
8 |
2 |
-10 |
18 |
1 |
1 |
-1 |
-2 |
0 |
2 |
4 |
1 |
1 |
1 |
-3 |
3 |
3 |
19 |
-2 |
2 |
-2 |
2 |
-3 |
2 |
5 |
1 |
1 |
1 |
2 |
2 |
2 |
20 |
-4 |
1 |
-4 |
2 |
-2 |
2 |
6 |
0 |
4 |
-3 |
2 |
-2 |
4 |
21 |
-2 |
5 |
-2 |
2 |
0 |
4 |
7 |
4 |
4 |
1 |
1 |
-2 |
2 |
22 |
1 |
5 |
1 |
1 |
3 |
1 |
8 |
2 |
2 |
2 |
4 |
4 |
-4 |
23 |
1 |
-2 |
1 |
2 |
-5 |
2 |
9 |
2 |
4 |
2 |
-2 |
0 |
2 |
24 |
2 |
-7 |
4 |
6 |
0 |
0 |
10 |
-4 |
-4 |
2 |
-2 |
4 |
-4 |
25 |
7 |
4 |
4 |
-1 |
1 |
-2 |
11 |
-1 |
-1 |
-3 |
-1 |
-3 |
3 |
26 |
-3 |
9 |
3 |
1 |
4 |
2 |
12 |
2 |
2 |
-5 |
1 |
0 |
0 |
27 |
5 |
13 |
5 |
2 |
0 |
4 |
13 |
2 |
2 |
3 |
2 |
1 |
1 |
28 |
2 |
-7 |
-4 |
2 |
-8 |
10 |
14 |
4 |
1 |
4 |
-2 |
-4 |
2 |
29 |
7 |
6 |
5 |
-2 |
0 |
-2 |
15 |
2 |
5 |
2 |
-1 |
-2 |
1 |
30 |
17 |
14 |
14 |
-2 |
-2 |
-4 |
Задача
17. Користуючись теорією квадратичних
форм, звести до канонічного вигляду
рівняння кривої
та
визначити її тип.
|
а |
b |
с |
d |
e |
f |
|
а |
b |
с |
d |
e |
f |
1 |
3 |
3 |
8 |
-2 |
2 |
5 |
16 |
0 |
0 |
4 |
4 |
4 |
1 |
2 |
2 |
2 |
-6 |
3 |
-2 |
5 |
17 |
1 |
1 |
-8 |
20 |
20 |
1 |
3 |
5 |
5 |
-2 |
1 |
-17 |
8 |
18 |
3 |
3 |
4 |
8 |
12 |
1 |
4 |
1 |
1 |
-8 |
12 |
12 |
3 |
19 |
4 |
4 |
2 |
12 |
12 |
1 |
5 |
4 |
4 |
-2 |
6 |
6 |
-9 |
20 |
0 |
0 |
2 |
2 |
2 |
-3 |
6 |
3 |
3 |
-4 |
4 |
4 |
1 |
21 |
1 |
-1 |
4 |
-8 |
-4 |
1 |
7 |
0 |
0 |
4 |
4 |
-4 |
1 |
22 |
-4 |
-4 |
2 |
10 |
-10 |
1 |
8 |
1 |
1 |
4 |
4 |
2 |
-5 |
23 |
-1 |
-1 |
-4 |
-4 |
-2 |
2 |
9 |
2 |
2 |
-2 |
6 |
-6 |
-6 |
24 |
0 |
0 |
4 |
4 |
-4 |
-2 |
10 |
0 |
0 |
-4 |
8 |
8 |
1 |
25 |
-3 |
-3 |
4 |
-6 |
4 |
2 |
11 |
3 |
3 |
2 |
-12 |
-4 |
1 |
26 |
-2 |
-2 |
2 |
-6 |
6 |
1 |
12 |
5 |
5 |
-2 |
10 |
-2 |
1 |
27 |
0 |
0 |
-2 |
-2 |
-2 |
1 |
13 |
0 |
0 |
-4 |
-4 |
4 |
6 |
28 |
-1 |
-1 |
4 |
2 |
-4 |
1 |
14 |
3 |
3 |
-4 |
6 |
-4 |
-7 |
29 |
2 |
2 |
-2 |
-2 |
-2 |
1 |
15 |
3 |
3 |
-2 |
-6 |
2 |
1 |
30 |
0 |
0 |
4 |
4 |
-4 |
0 |
Задача 18. Обчислити границі числових послідовностей.
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
|
6 |
|
|
|
7 |
|
|
|
8 |
|
|
|
9 |
|
|
|
10 |
|
|
|
11 |
|
|
|
12 |
|
|
|
13 |
|
|
|
14 |
|
|
|
15 |
|
|
|
16 |
|
|
|
17 |
|
|
|
18 |
|
|
|
19 |
|
|
|
20 |
|
|
|
21 |
|
|
|
22 |
|
|
|
23 |
|
|
|
24 |
|
|
|
25 |
|
|
|
26 |
|
|
|
27 |
|
|
|
28 |
|
|
|
29 |
|
|
|
30 |
|
|
|
Задача 19. Обчислити границі функцій, користуючись відомими границями функцій та наслідками з них.
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
|
6 |
|
|
|
7 |
|
|
|
8 |
|
|
|
9 |
|
|
|
10 |
|
|
|
11 |
|
|
|
12 |
|
|
|
13 |
|
|
|
14 |
|
|
|
15 |
|
|
|
16 |
|
|
|
17 |
|
|
|
18 |
|
|
|
19 |
|
|
|
20 |
|
|
|
21 |
|
|
|
22 |
|
|
|
23 |
|
|
|
24 |
|
|
|
25 |
|
|
|
26 |
|
|
|
27 |
|
|
|
28 |
|
|
|
29 |
|
|
|
30 |
|
|
|
Задача 20. Знайти
точки розриву функції
,
якщо вони існують, та визначити їхній
характер. Побудувати схематично графік
функції.
1 |
|
16 |
|
2 |
|
17 |
|
3 |
|
18 |
|
4 |
|
19 |
|
5 |
|
20 |
|
6 |
|
21 |
|
7 |
|
22 |
|
8 |
|
23 |
|
9 |
|
24 |
|
10 |
|
25 |
|
11 |
|
26 |
|
12 |
|
27 |
|
13 |
|
28 |
|
14 |
|
29 |
|
15 |
|
30 |
|
Зразок розв’язання індивідуальних домашніх завдань
Задача 1. Виконати дії. Представити результат в алгебраїчній формі
.
Решение
Обчислимо спочатку
.
Тоді маємо:
.
Задача 2. Виконати дії Представити результат у показниковій та алгебраїчній формі
.
Решение
Знайдемо модулі та аргументи комплексних чисел
,
,
.
Запишемо всі числа у показниковій формі:
.
Подальші дії виконаємо у показниковій формі. Для переходу до алгебраїчної форми скористаємось формулою Ейлера:
.
Задача
3. Обчислити
всі значення
та
побудувати їх на площині комплексного
змінного.
Решение
Обчислимо
модуль та аргумент комплексного числа
:
.
Скористаємось формулою для обчислення кореня з комплексного числа
.
Одержимо
.
Знайдемо чотири значення кореня:
,
,
,
.
Всі значення лежать на одиничному колі з центром к нульовій точці та поділяють його на чотири рівні частини.
Задача
4. Побудувати
на площині комплексного змінного множину
точок, які
задовольняють умові
.
Решение
Для
одержання даної умови у декартових
координатах підставимо
у ліву частину нерівності.
Маємо:
.
Задана умова приймає вигляд
або
.
Виділяючи
повний квадрат за змінною
,
одержимо:
.
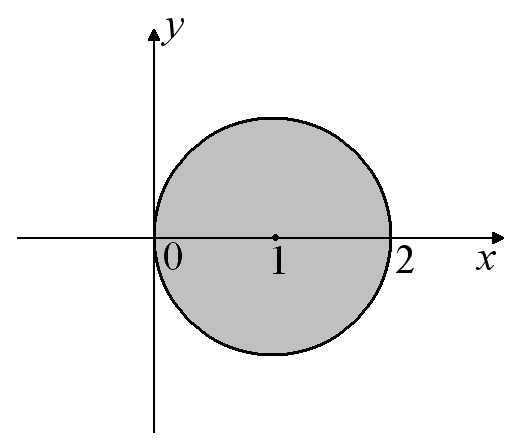
Шукана
множина є одиничним колом з центром
у
точці
.
Побудуємо
його на малюнку.
Задача 5. Розв'язати систему лінійних неоднорідних алгебраїчних рівнянь: 1) за правилом Крамера; 2) методом Жордана – Гауса; 3) за допомогою оберненої матриці.
Розв’язання
1) Розв'яжемо систему рівнянь за правилом Крамера. Складемо визначник з коефіцієнтів лівої частини системи:
.
Оскільки
,
система має єдиний розв'язок, який
знаходиться за формулами
,
де
визначники
,
,
та
утворюються з визначника
заміною стовпця коефіцієнтів при
відповідній змінній на стовпець вільних
членів.
;
;
.
2) Розв'яжемо систему рівнянь методом Жордана – Гауса. Запишемо розширену матрицю системи та зведемо її до діагонального вигляду методом елементарних перетворень. Спочатку віднімемо з другого рядка подвоєний перший та з третього рядка перший, скоротимо одержані рядки:
Поміняємо місцями другий та третій рядки і віднімемо з третього рядка подвоєний другий, далі віднімемо останній рядок з перших двох, скоротимо одержані рядки:
.
Отже,
розв’язок системи:
.
3) Розв'яжемо систему за допомогою оберненої матриці. Позначимо
– матрицю-стовпець
невідомих,
– матрицю коефіці-єнтів при невідомих,
– матрицю-стовпець вільних членів. За
допомо-гою цих матриць запишемо систему
рівнянь у матричній формі:
,
звідки одержимо
.
Знайдемо
обернену матрицю
.
Визначник матриці
,
отже, матриця A
невироджена і має обернену матрицю, а
система рівнянь є визначеною. Складемо
транспоновану матрицю:
.
Обчислимо алгебраїчні доповнення елементів цієї матриці і запишемо їх у приєднану матрицю:
.
Таким
чином, обернена матриця має вигляд
.
Запишемо розв'язок системи у вигляді
.
Задача 3. Дана система лінійних однорідних алгебраїчних рівнянь
Знайти фундаментальну систему розв'язків та загальний розв'язок цієї системи.