3.5 Пример выполнения и оформления задания

Найдем положительный корень уравнения

(3.4)

тремя рассмотренными приближенными методами с точностью .

1. О

   

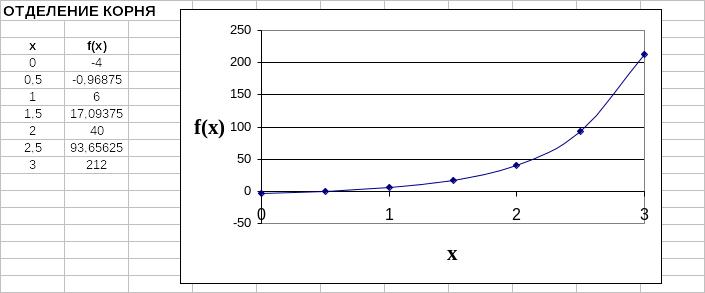
   Рис. 3.4

   тделение корней. Вначале нужно отделить корень. В Excel это можно сделать графически. В одном из столбцов зададим значения переменной , а в соседнем вычислим значения функции (рис.3.4). С помощью Мастера диаграмм построим график этой функции: в меню выбираем блок «Вставка», затем «Диаграмма», для графика функции используем «точечную» диаграмму.

По графику видно, что корень находится примерно между 0 и 1. По таблице значений функции можно указать более точный отрезок: [0,5;1], так как , а . Положительный корень уравнения (3.4) будем искать на отрезке [0,5;1].

2. Метод деления отрезка пополам.

На листе Excel создадим таблицу, содержащую номер итерации , левую и правую границы -го отрезка, его середину , значения функции на границах и в середине отрезка , а также меру расхождения между двумя значениями корня на соседних итерациях (рис.3.5).

З

Рис. 3.5

ададим начальные значения и , вычислим их полусумму . Найдем значения функции в этих точках. Так как и , то на следующей итерации рассматриваем отрезок , где , (рис. 3.5).

Продолжаем процесс до тех пор, пока не выполнится условие . Таким образом, на 12-том шаге получаем .

3. Метод Ньютона.

Вычислим производную функции: . Создадим таблицу, содержащую номер итерации , - приближенное значение корня на -той итерации, значение функции и ее производной в точке : и , а также меру расхождения между двумя значениями корня на соседних итерациях (рис.3.6).

В

Рис. 3.6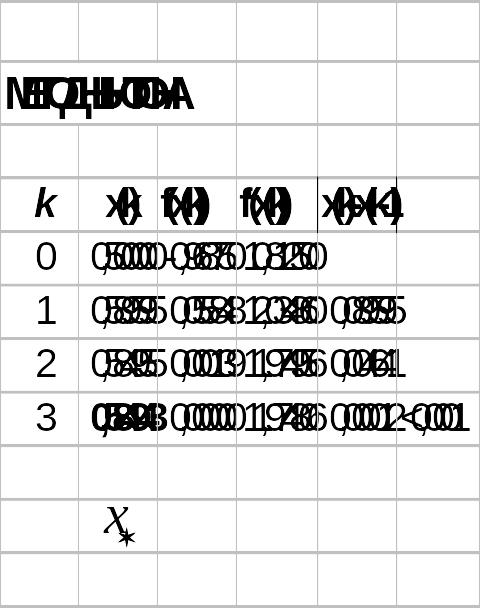

качестве начального приближения возьмем . Каждое последующее значение вычислим по формуле (3.2). Заполняем таблицу до тех пор, пока не выполнится условие (рис. 3.6).

На третьем шаге получим .

4. Метод линейной интерполяции.

Т

Рис. 3.7

ак же, как и в методе деления отрезка пополам, создадим таблицу, содержащую номер итерации , левую и правую границы -го отрезка, точку пересечения секущей с осью абсцисс, значения функции на границах отрезка и в точке , а также меру расхождения между двумя значениями корня на соседних итерациях (рис.3.7).

Начальный отрезок возьмем тот же – [0,5;1]. Значение вычислим по формуле (3.3). Найдем значения функции в точках . Так как и , то на следующей итерации рассматриваем отрезок , где , (рис. 3.7).

Продолжаем процесс до тех пор, пока не выполнится условие . На 4-той итерации получаем .

4. Сравнение результатов. Значения корней, полученные тремя методами, а также количество потребовавшихся итераций приведены в таблице 3.2. Как видим, меньше всего шагов понадобилось в методе Ньютона. Но его существенным недостатком является необходимость вычислять производную, что зачастую представляет собой нелегкую задачу. Медленнее всего сходится метод деления отрезка пополам. Значения корней приближенно равны. В последней строке таблицы указано значение корня, найденное с помощью процедуры Подбор параметра.

Таблица 3.2

Метод	Значение корня	Количество итераций
Деления отрезка пополам	0,58490 ≈ 0,5849	12
Ньютона	0,58494 ≈ 0,5849	3
Линейной интерполяции	0,58493 ≈ 0,5849	4
Подбор параметра	0,58496 ≈ 0,5850