3.3. Вибрация механической системы с распределенными параметрами при внешней периодической нагрузке.

Рассмотрим систему с распределенными параметрами, допускающую получение аналитического решения.

В качестве примера рассмотрим трубопровод, находящийся под воздействием сил инерции, упругой реакции материала трубы, демпфирования и внешней периодической нагрузки. Считаем, что трубопровод представляет собой балку на двух опорах. Как и выше, используем модель вязкого демпфирования. Уравнение движения системы будет иметь вид

,

(87)

где f(x,t) - внешняя нагрузка.

Решение этого уравнения в явной форме состоит из двух частей:

,

где  ‑ общее решение однородного уравнения (без правой части);

 ‑ частное решение неоднородного уравнения (с правой частью).

На основании изложенного выше считаем, что решение определяет свободные колебания системы, зависящие от начальной формы искривления и от скоростей, сообщаемых в начальный момент времени элементам системы. Эти колебания вследствие наличия демпфирования затухают со временем и остаются лишь вынужденные колебания. Рассмотрим решение .

Рассмотрим случай жесткого закрепления концов. Определим выражение для фундаментальных функций Х_n.

Введем новые обозначения для фундаментальной функции

,

где А, В, С, D ‑ постоянные интегрирования.

S(x), Т(х), U(x) V(x) ‑ Функции Крылова, определяемые по выражениям:

; ;

; ;

При использовании функций Крылова полезно иметь в виду следующие их свойства:

Производные от функций Крылова приведены в табл. 10.

Таблица 10

Производные от функций Крылова

Функция	Первая	Вторая	Третья	Четвертая
S	rV	r2U	r3Т	r4S
Т	rS	r2V	r3U	r4T
U	rТ	r2S	r3V	r4U
V	rU	r2T	r3S	r4V

Функции Крылова позволяют сразу написать общий интеграл, удовлетворяющий граничным условиям на конце х=0. Для жесткого закрепления концов трубопровода длиной l

.

Тогда общий интеграл уравнения для фундаментальных функций будет иметь вид

,

(88)

который удовлетворяет всем граничным условиям при х=0:

.

Постоянные С и D находим из условия на конце х=1:

.

(89)

Данная система уравнений является однородной относительно неизвестных С и D. Чтобы она имела решения, отличные от нуля, коэффициент r должен иметь значения, приведенные в параграфе 2.2, для соответствующего условия закрепления.

Уравнение соответствующей собственной формы составим следующим образом. Из первого или второго уравнения (89) получаем

.

(90)

Подставив отношение (90) в уравнение форм колебаний (88), получим

.

Отсюда следует, что собственная форма колебании определяется с точностью до постоянного множителя.

Теперь рассмотрим случай воздействия на систему внешней сосредоточенной гармонической нагрузки приложенной в точке х=а.

Для этого случая имеем

.

(91)

при условии, что когда .

Решение уравнения (87) будем искать по методу А.Н.Крылова в виде разложения в ряд по фундаментальным функциям , получаемым для балки без учета затухания

,

(92)

где функции зависят от условий закрепления концов трубопровода-балки.

Подставляя в виде (92) в уравнение (87), выраженное в безразмерных координатах

,

(93)

и принимая во внимание, что

,

(93)

получим

,

где - собственная частота, соответствующая i-му тону.

Умножая обе части последнего выражения на и интегрируя в пределах от 0 до 1, получим

,

где

,

так как вследствие условия ортогональности для фундаментальных функций в левой части все члены, содержащие произведение функций , пропадут.

Для

,

получим, согласно условию (91)

.

Значение

.

может быть взято из табл. 11.

Таблица 11

Значения интегралов при различных видах условий закрепления

х=0	х=1	I	II
Заделан	Заделан
Оперт	Оперт

Таким образом, для после разложения получим следующие значения:

- для идеального шарнирного опирания обоих концов;

для идеально жесткого закрепления обоих концов.

Тогда для чисто вынужденных колебаний согласно решению уравнения (87) соответственно получим:

идеальное шарнирное опирание обоих концов:

;

(94)

идеально жесткое закрепление обоих концов:

,

(95)

где

Из выражений (94) и (95) следует, что амплитуда вынужденной вибрации достигает своего максимального значения при выполнении условия

,

(96)

Поэтому в механической системе с распределенными параметрами без демпфирования, то есть , если частота внешней возмущающей нагрузки стремится к одной из частот собственных колебаний , то амплитуда вынужденных колебаний неограниченно возрастает.

Если система обладает демпфированием , то при выполнении условия (96) амплитуда гармонических колебаний механической системы достигает своего максимального значения, но ее величина ограничена и является функцией коэффициента демпфирования .

Таким образом, принципиальные выводы относительно условий резонанса и закона движения механической системы под действием внешней возмущающей периодической нагрузки одномассовой и многомассовой механических систем и системы с распределенными параметрами в условиях резонанса совпадают.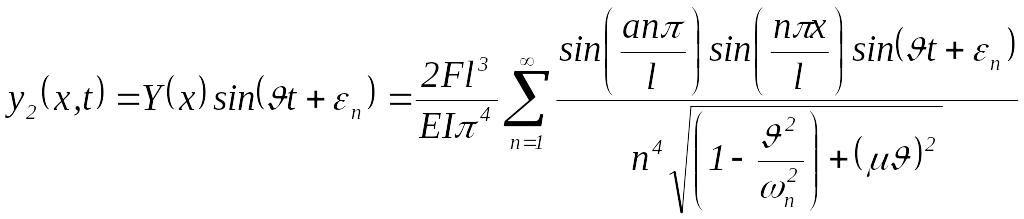