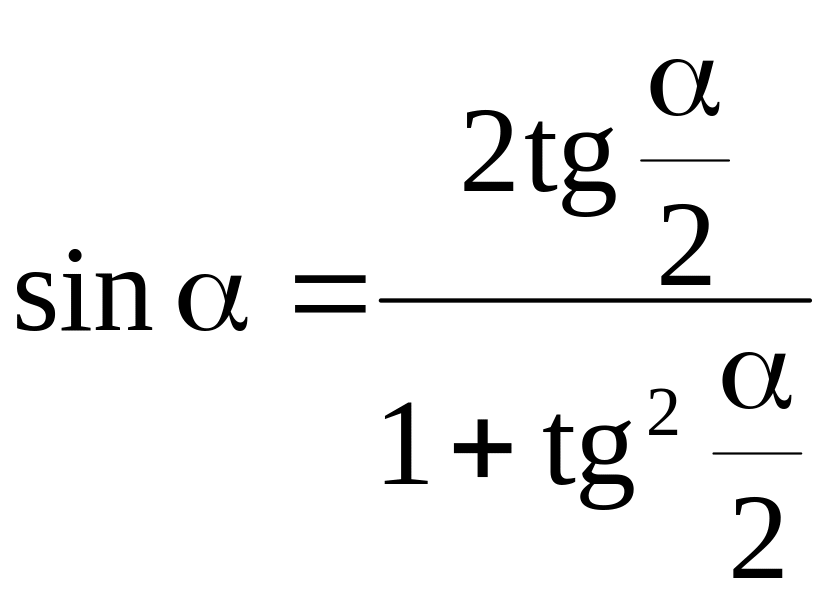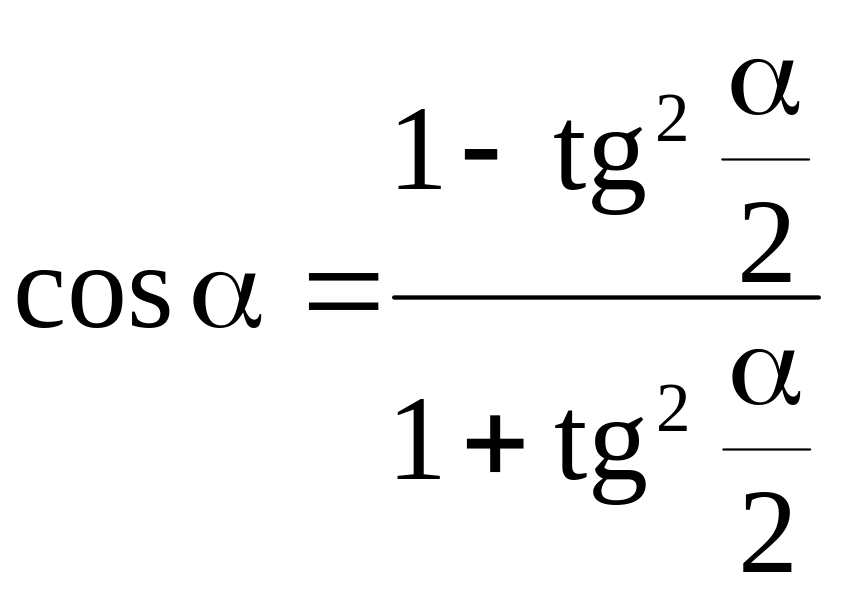Группа с
1. Найти
,
если
.
(Ответ:
.)
2. Вычислить
.
(Ответ:
.)
3. Вычислить
.
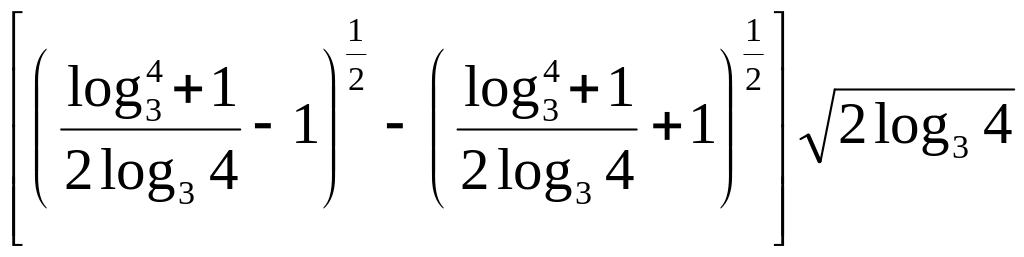(Ответ:
.)
4. Найти
,
если
.
(Ответ:
.)
5. Найти
,
если
,
.
(Ответ:
.)
6. Найти значение
выражения
.
(Ответ:
4.)
Решить уравнение (7-10)
7.
.
(Ответ:
.)
8.
.
(Ответ:
.)
9.
.
(Ответ:
.)
10.
.
(Ответ:
.)
Решить неравенство (11-14)
11.
.
(Ответ:
.)
12.
.
(Ответ:
.))
13.
.
(Ответ:
.)
14.
.
(Ответ:
.)
8. Тригонометрия
8.1. Преобразование тригонометрических выражений
Определение
8.1.
Числовой
единичной окружностью
называют окружность
,
у которой точка
- начало отсчета, положительное направление
отсчета – против часовой стрелки,
единичный отрезок – часть дуги окружности,
длина которой равна длине радиуса
окружности.
Определение 8.2. Один радиан равен центральному углу окружности, длина дуги которого равна радиусу этой окружности.
,
.
рис. 8.1 |
Между множеством
действительных чисел и множеством
точек числовой окружности установлено
соответствие: каждому действительному
числу
соответствует точка
|
числовой окружности, что длина дуги
равна
,
а каждая точка окружности соответствует
бесконечному множеству чисел вида
,
- длина одной из
дуг, соединяющих точки
и
.
Любая точка
на числовой окружности имеет декартовы
координаты
(рис. 8.1).
- ордината точки
;
,
- абсцисса точки
;
.
Углы в градусах |
|
|
|
|
|
|
|
|
Углы в радианах |
|
|
|
|
|
|
|
|
Значение тригонометрических функций некоторых углов
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
1 |
0 |
|
|
1 |
|
|
|
0 |
|
0 |
|
0 |
|
1 |
|
- |
0 |
- |
|
- |
|
1 |
|
0 |
- |
0 |
Основные тригонометрические тождества
|
|
|
|
Формулы суммы и разности аргументов
|
|
|
|
|
|
Формулы двойного и тройного аргументов
|
|
|
|
|
|
|
|
|
|
Выражение тригонометрических функций через тангенс половинного угла
Если
,
,
то
|
|
Преобразование суммы и разности тригонометрических
функций в произведение
|
|
|
|
|
|
Также бывает удобно использовать следующие преобразования.
|
(8.1) |
где
,
а
определяется из формул
;
.
|
(8.2) |
где
,
а
определяется из формул
;
.
Преобразование произведения тригонометрических функций в сумму
|
|
|
|
