7.3. Логарифмические неравенства
Решение логарифмических неравенств основано на свойствах монотонности логарифмической функции.
Перечислим некоторые методы решения логарифмических неравенств.
1. При
неравенства вида
.
При
.
2. Замена переменной.
Пример 7.19.
Решить неравенство
.
Решение. Так
как основание логарифмов
,
то исходное неравенство равносильно
системе:
Ответ:
Пример 7.20.
Решить неравенство
.
Решение. Заметим, что
,
тогда
.
Ответ:
.
Пример 7.21.
Решить неравенство
.
Решение. Так
как
,
то
.
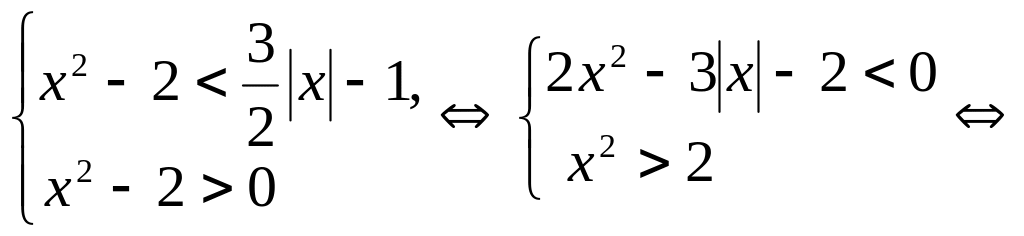
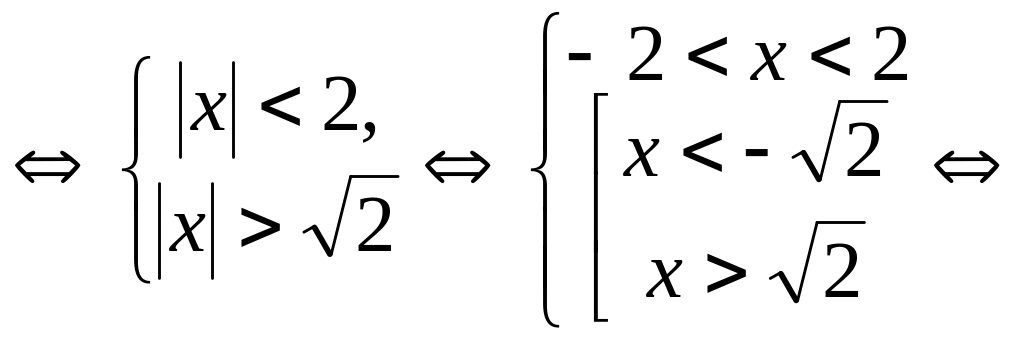
Ответ:
.
Пример 7.22.
Решить неравенство
.
Решение. Область
определения данного неравенства:
.
.
Сделаем замену:
,
тогда
.
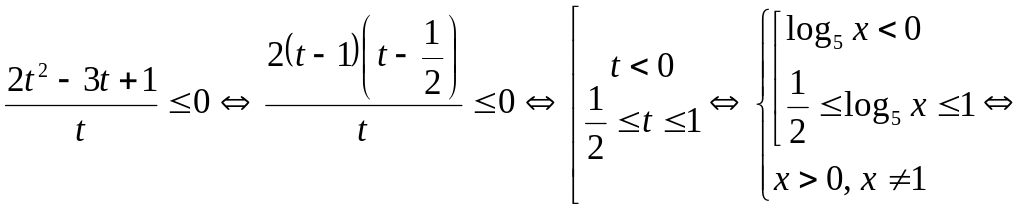
Ответ:
.
Пример 7.23.
Решить неравенство
.
Решение. Рассмотрим два случая.
1. Если
,
то
,
нет решений.
2. Если
,
то
.
Ответ:
.
Задачи для самостоятельного решения Группа а
Вычислить (1-6)
1.
.
(Ответ:
.)
2.
.
(Ответ:
.)
3.
.
(Ответ:
.)
4.
.
(Ответ:
.)
5.
.
(Ответ:
.)
6.
.
(Ответ:
.)
Решить уравнение (7-11)
7.
.
(Ответ:
.)
8.
.
(Ответ:
.)
9.
.
(Ответ:
.)
10.
.
(Ответ:
.)
11.
.
(Ответ:
.)
Решить неравенство (12-16)
12.
.
(Ответ:
.)
13.
.
(Ответ:
.)
14.
.
(Ответ:
.)
15.
.
(Ответ:
.)
16.
.
(Ответ:
.)
Группа b
Вычислить (1-7)
1.
.
(Ответ:
.)
2.
.
(Ответ:
.)
3.
.
(Ответ:
.)
4.
.
(Ответ:
.)
5. Найти
,
если
.
(Ответ:
.)
6.
.
(Ответ:
.)
7.
.
(Ответ:
.)
Решить уравнение (8-12)
8.
.
(Ответ:
.)
9.
.
(Ответ:
.)
10.
.
(Ответ:
.)
11.
.
(Ответ:
.)
12.
.
(Ответ:
.)
Решить неравенство (13-17)
13.
.
(Ответ:
.)
14.
.
(Ответ:
.)
15.
.
(Ответ:
.)
16.
.
(Ответ:
.)
17.
.
(Ответ:
.)