Свойства логарифмов
Пусть
.
Основное логарифмическое тождество:
.
Логарифм произведения, частного и степени:
;
четное
целое.
Формула перехода к новому основанию. Пусть
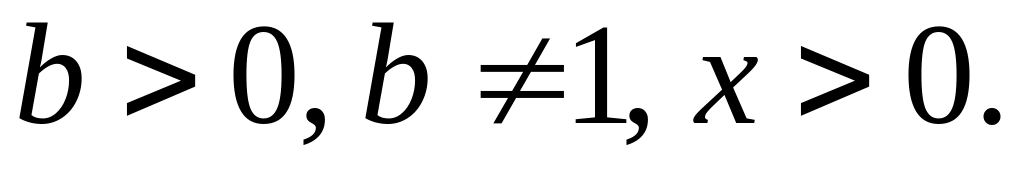Тогда
,
в частности,
,
при
.
Кроме того,
.
Пусть
,
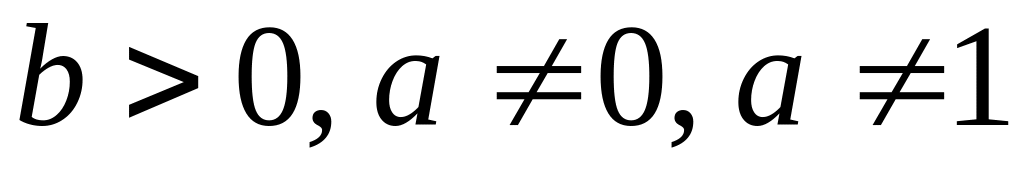тогда
,
;
,
целое
четное.
.Для любого положительного числа существует, и притом только одно, такое действительное число
,
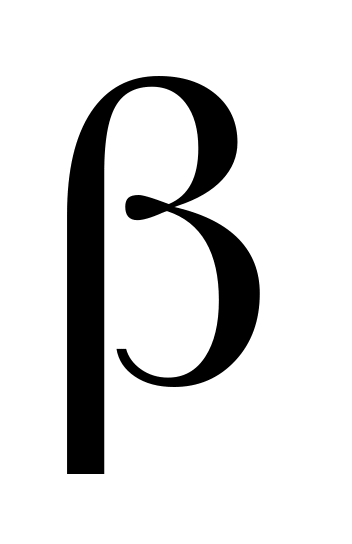что
.Из равенства
следует, что
(и наоборот).
Пример 7.1.
Вычислить: a)
;
б)
;
в)
;
г)
;
д)
;
е)
.
Решение.
а)
;
б)
;
в)
;
г)
;
д)
;
е)
.
Ответ:
а)
;
б)
;
в)
;
г) 0; д)
;
е)
.
Пример 7.2.
Вычислить: a)
;
б)
;
в)
;
г)
;
д)
;
е)
.
Решение.
а)
б)
;
в)
;
г)
;
д)
;
е)
.
Ответ: а)
3; б) 1; в) 8; г) 1; д)
;
е)
.
Пример 7.3.
Вычислить
.
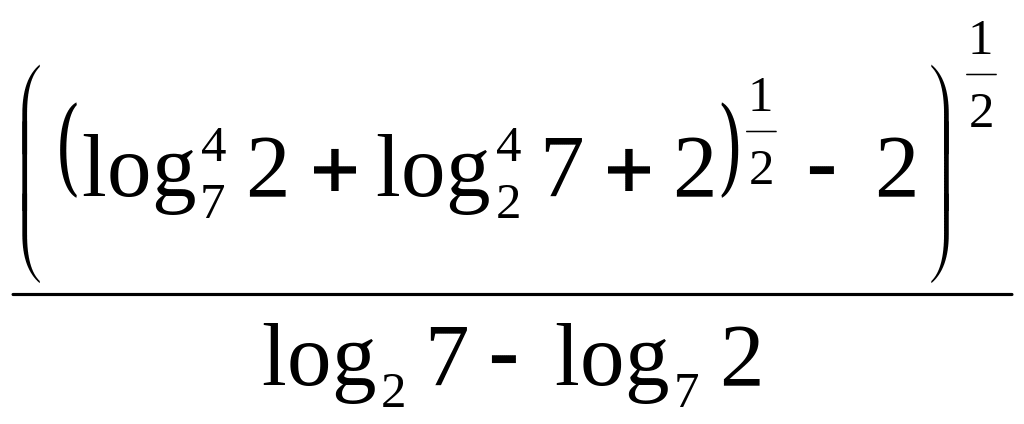Решение.
.
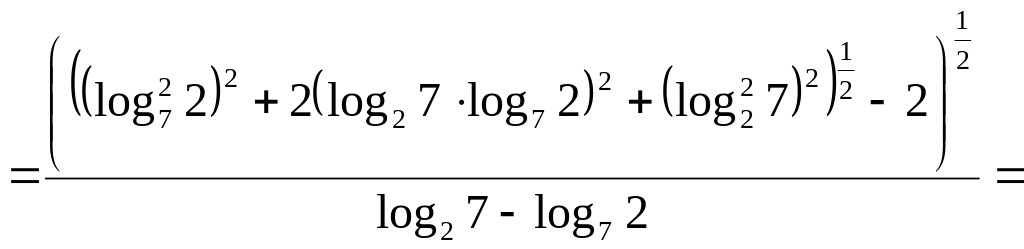
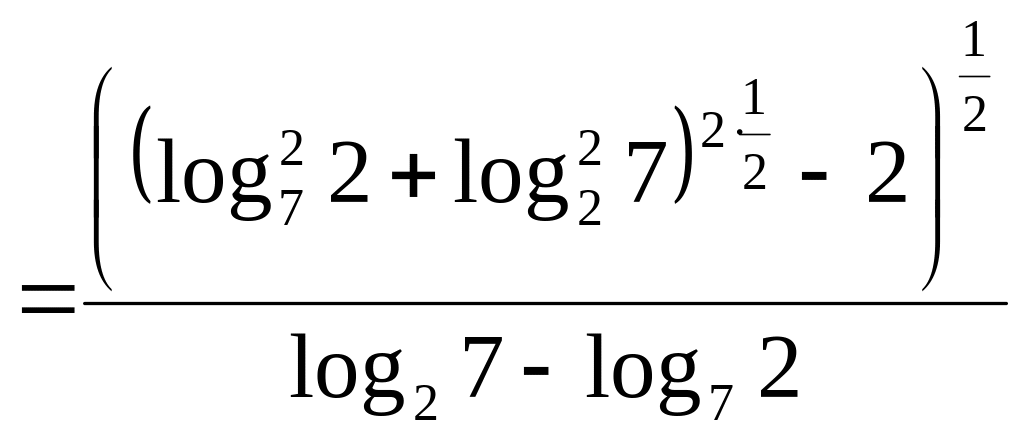
Ответ: 1.
Пример 7.4.
Найти
,
.
Решение.
.
Ответ: 8.
Пример 7.5.
Вычислить
.
Решение.
.
Ответ: 1.
Пример 7.6.
Вычислить
.
Решение.
.
Ответ:
.
Пример 7.7.
Вычислить
.
Решение.
Ответ: 4.
Пример 7.8.
Вычислить
.
Решение.
.
Ответ: 7.
Пример 7.9.
Вычислить
.
Решение.
.
Ответ:
.
Пример 7.10.
Вычислить
.
Решение.
.
Ответ: 48.
Пример 7.11.
Найти значение выражения
,
если
.
Решение.
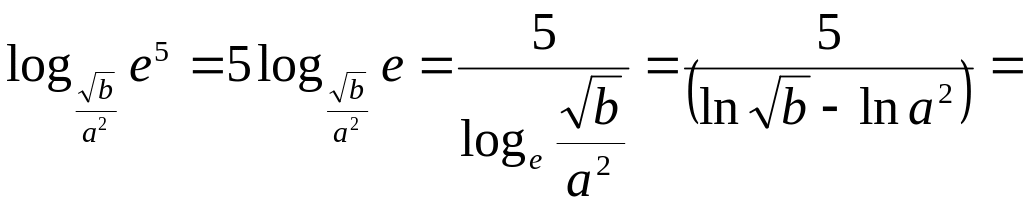
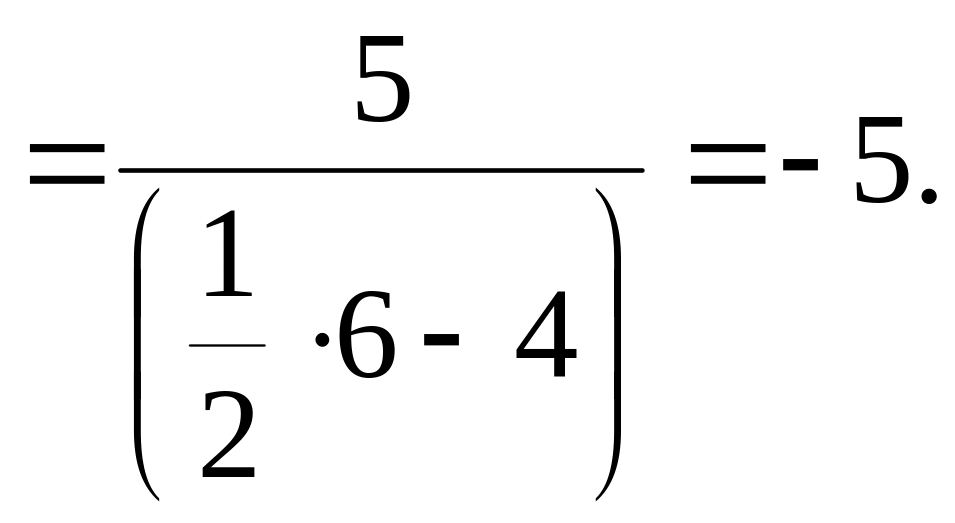
Ответ:
.
7.2. Логарифмические уравнения
Выделим некоторые методы решения логарифмических уравнений.
1. Логарифмические уравнения, решаемые по определению логарифма.
.
2. Уравнения вида
.
3. Уравнения первой
степени относительно логарифма, решаемые
потенцированием. Уравнения вида
равносильны каждой из следующих систем:
или
,
выбирают ту систему, которая проще для решения.
4. Уравнения вида
равносильно системе
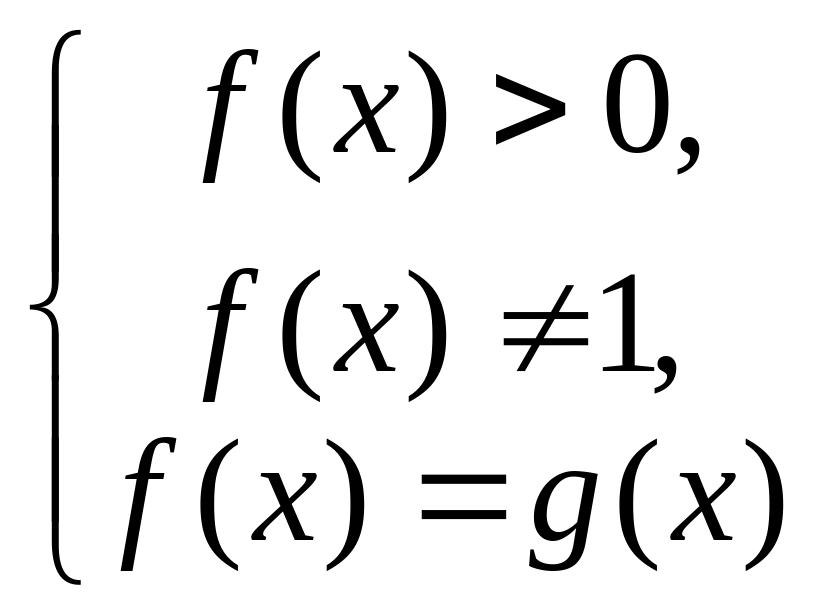или
.
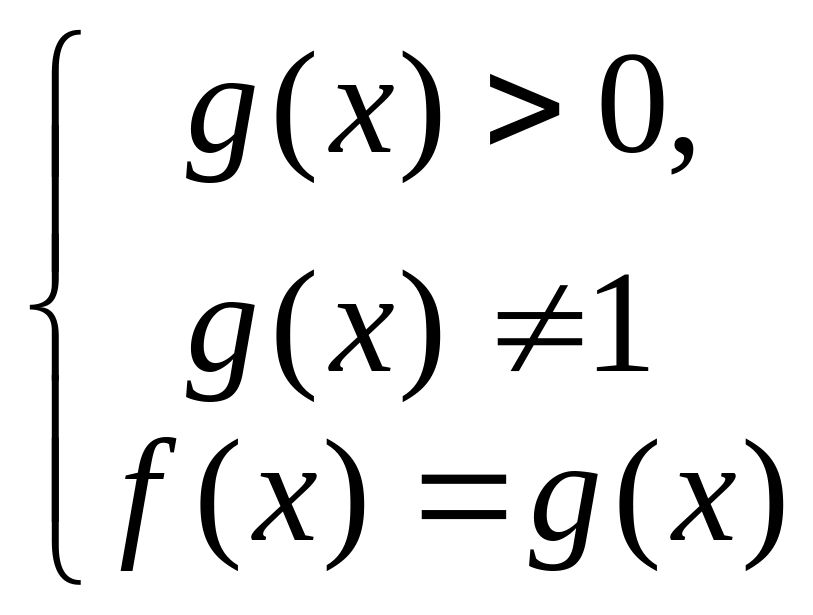5. Применение свойств логарифмов: произведения, частного и степени.
6. Переход к одному основанию в уравнениях, содержащих логарифмы с различными основаниями. Отметим, что предпочтительнее переходить к основанию, не содержащему переменной, чтобы не потерять корни уравнения.
7. Замена переменной.
8. Функциональный метод.
Замечание 7.2. Формальное использование перечисленных выше методов может привести к изменению ОДЗ уравнения. При нетождественных преобразованиях уравнения необходимо сделать проверку.
Пример 7.12.
Решить уравнение
.
Решение.
Ответ: 2; 9.
Пример 7.13.
Решить уравнение
.
Решение.
.
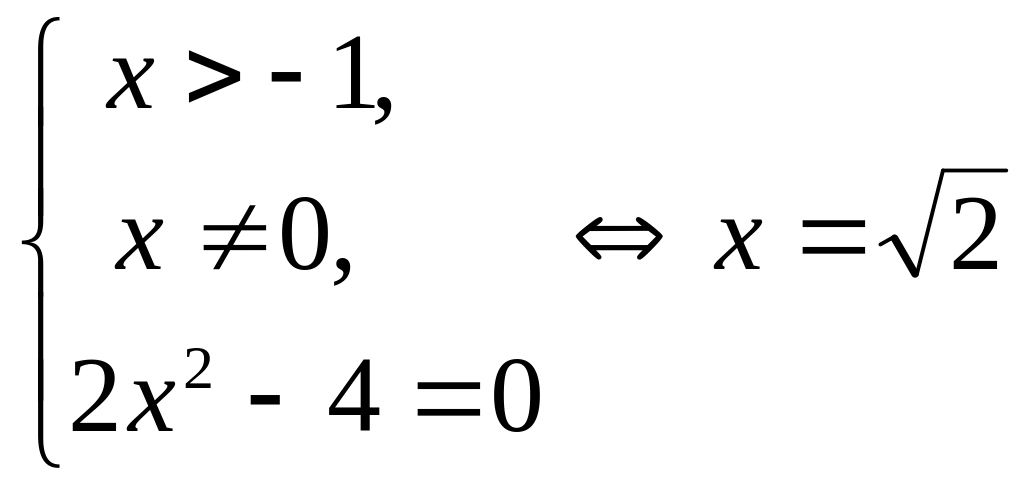Ответ:
.
Пример 7.13.
Решить уравнение
.
Решение.
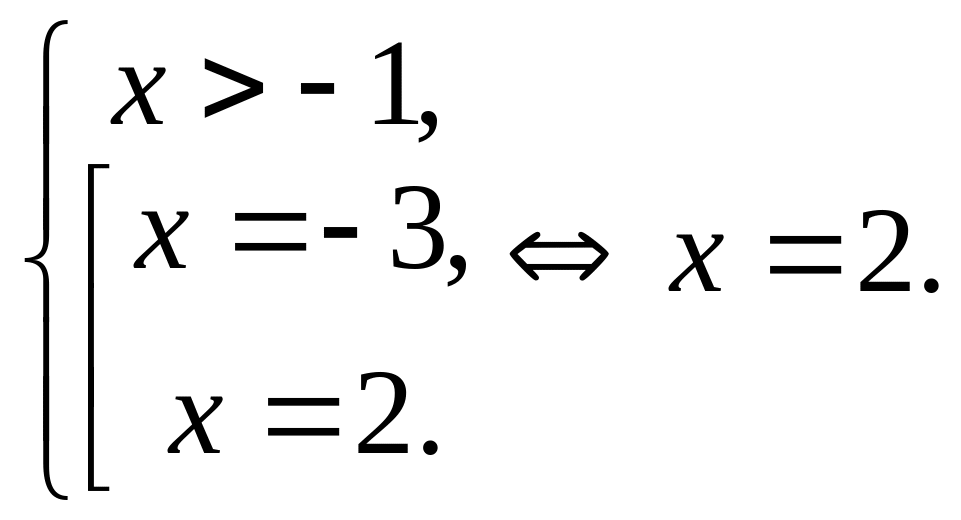
Ответ: 2.
Пример 7.14.
Решить уравнение
Решение. Преобразуем логарифмы, стоящие в левой части уравнения:
.
.
Исходное уравнение будет равносильно системе
.
Введем замену
,
тогда
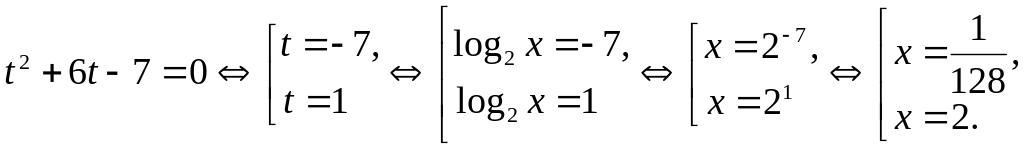
Ответ: 2;
.
Пример 7.15.
Решить уравнение
.
Решение. Учитывая,
что
,
прологарифмируем обе части уравнения
по основанию 10:
.
Ответ: 0,1;
.
Пример 7.16.
Решить уравнение
.
Решение.
.
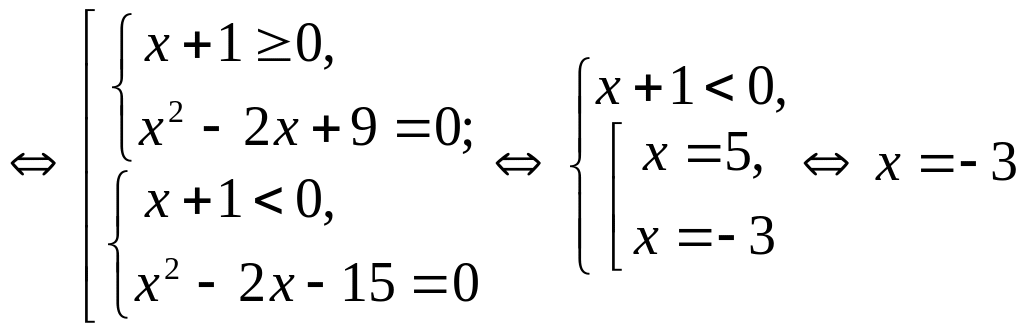Ответ:
.
Пример 7.17.
Решить уравнение
.
Решение.
Ответ:
.
Пример 7.18.
Решить уравнение
Решение.
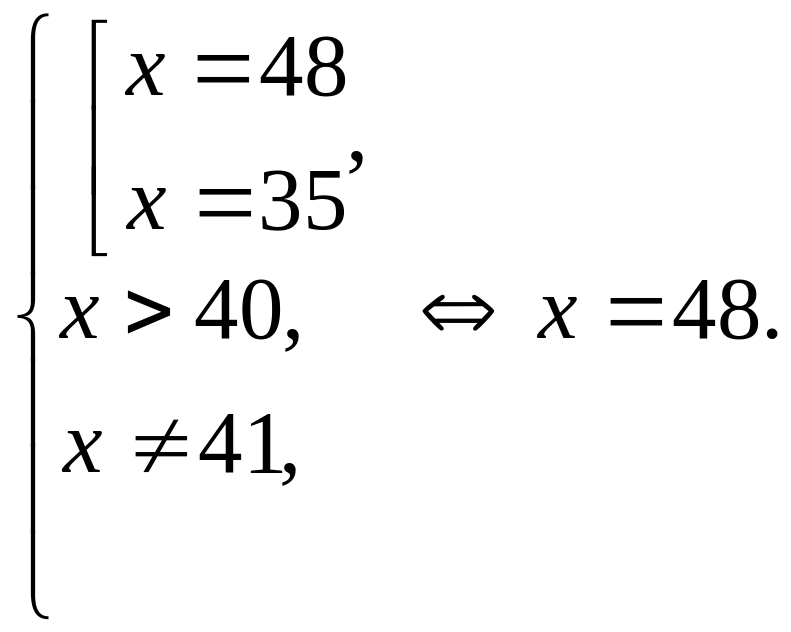
Ответ: 48.
Пример 7.18.
Решить уравнение
Решение.
.
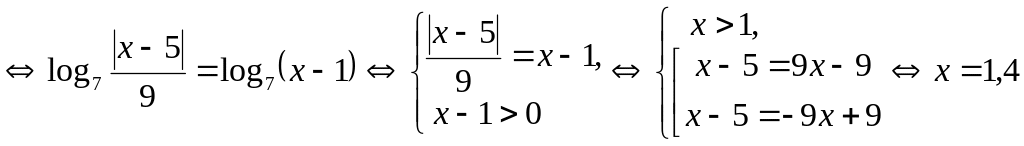Ответ: 1,4.