4.5. Уравнения с модулем
Рассмотрим уравнения, содержащие знак модуля. В зависимости от расположения знака модуля можно провести классификацию таких уравнений. Рассмотрим некоторые виды уравнений с модулем и методы их решения.
1.
2. Для решения
уравнения вида
используют два способа:
а)
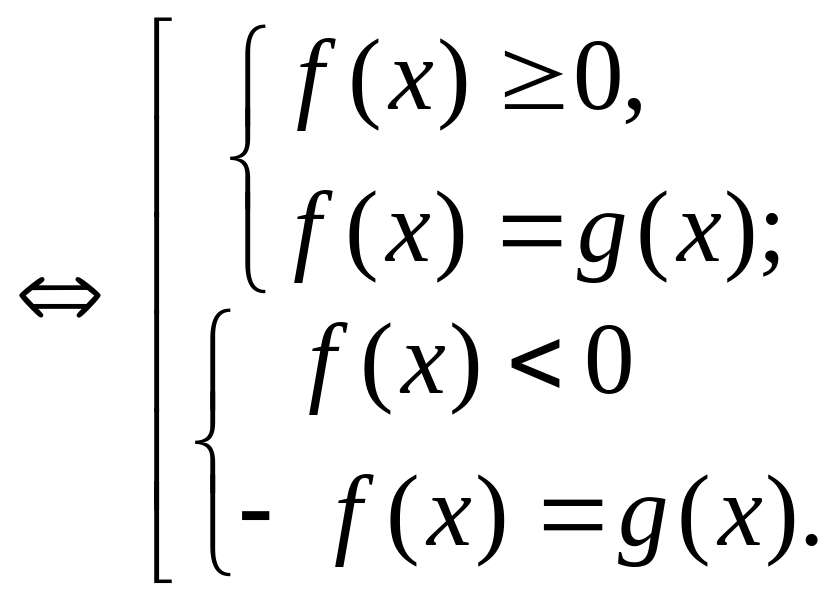
б)
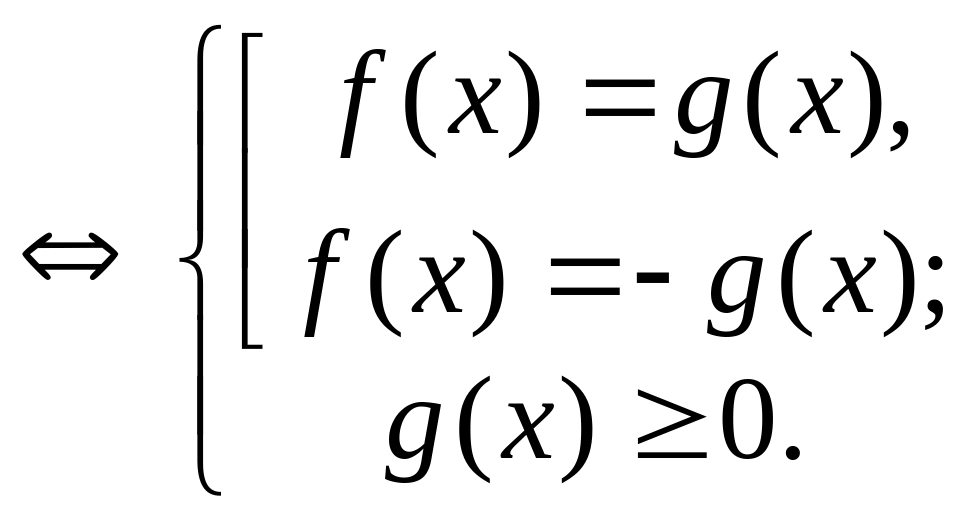
Замечание
4.4. Выбор
способа a)
или б)
зависит от того, какое из неравенств
или
легче решить.
3.
4. Уравнение вида
можно решить, используя замену
.
Пример 4.18. Решить
уравнение
.
Решение.
.
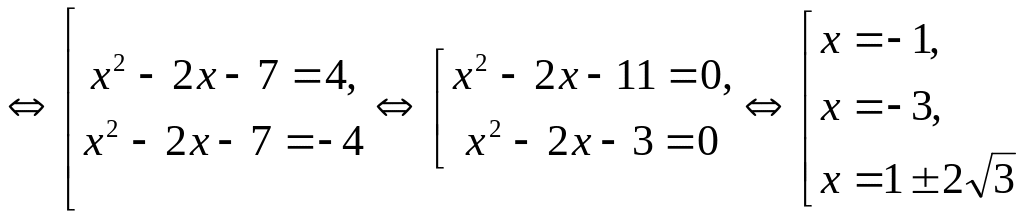Ответ:
.
Пример 4.19. Решить
уравнение
.
Решение.
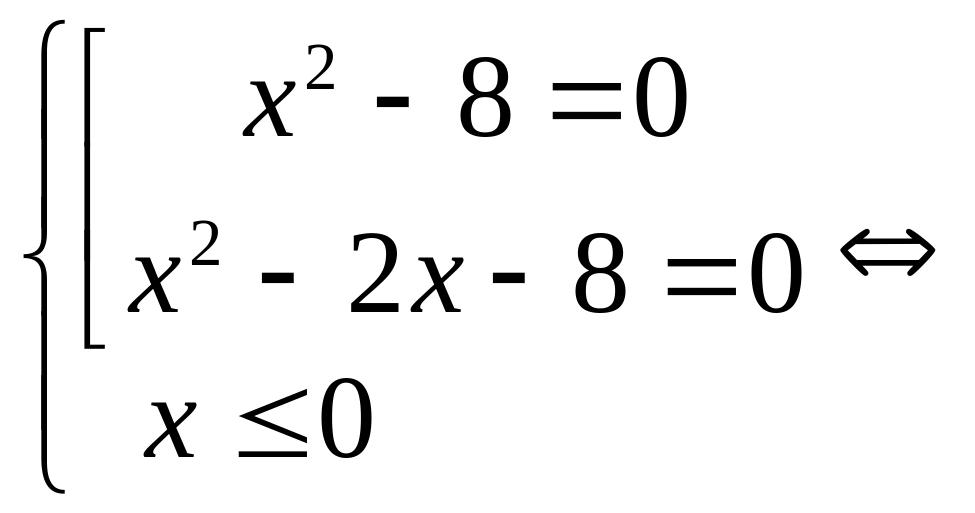
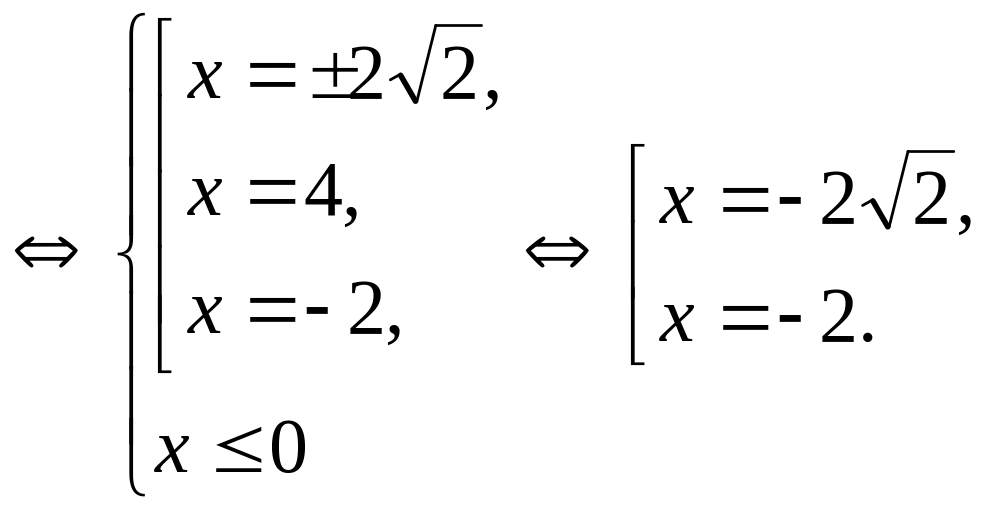
Ответ:
.
Пример 4.20. Решить
уравнение
Решение. Так как функция, стоящая под знаком модуля проще, то при решении исходного уравнения перейдем к совокупности двух систем:
.
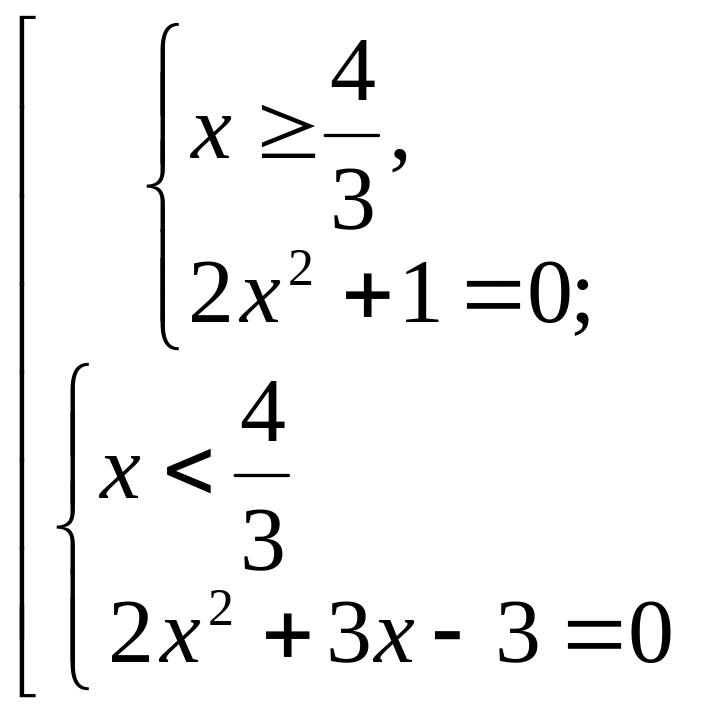Уравнение
действительных корней не имеет. Решая
вторую систему совокупности, получим
Ответ:
.
Пример 4.21. Решить
уравнение
Решение.
Ответ:
.
Ответ:
.
Пример 4.22. Решить
уравнение
Решение. В
силу свойства модуля
,
тогда
исходное уравнение примет вид
Сделаем замену
тогда
.
Пример 4.23. Решить
уравнение
.
Решение.
.
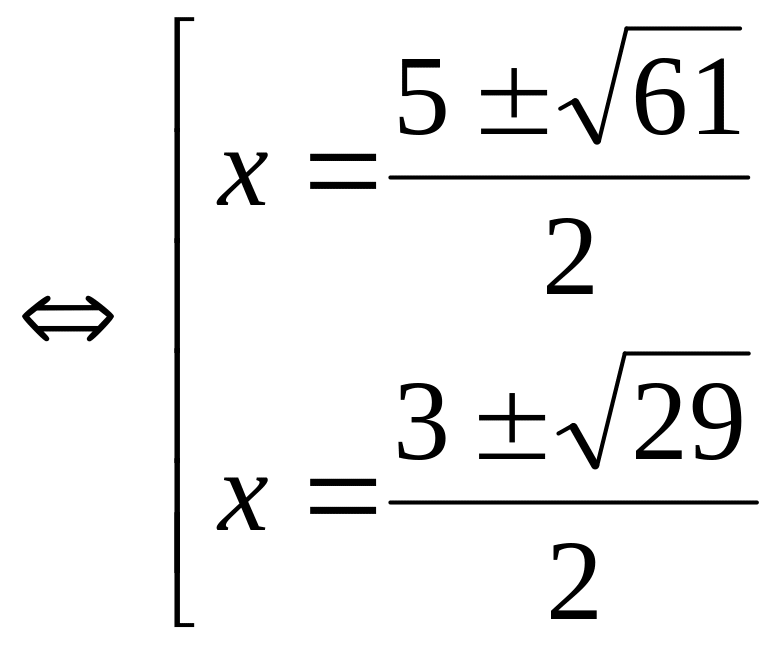Ответ:
;
.
Пример 4.24. Решить
уравнение
.
Решение.
Ответ:
;
.
Пример 4.25. Решить
уравнение
.
Решение.
.
Ответ:
;
.
Пример 4.26. Решить
уравнение
.
Решение.
.
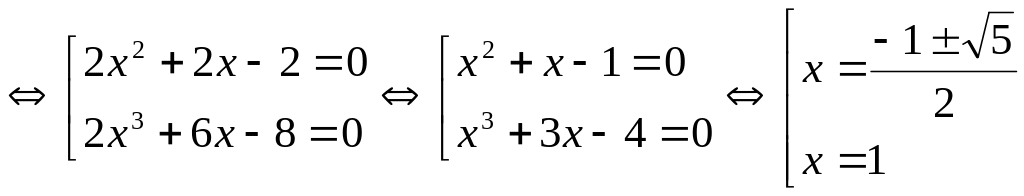Ответ:
;
.
Пример 4.27. Решить
уравнение
.
Решение. Так
как
,
то
.
Ответ: .
Пример 4.28. Решить
уравнение
.
Решение. Для решения уравнения, расставим предварительно знаки выражений, стоящих под знаком модуля, на промежутках:
Раскроем модули и получим соответствующие уравнения на указанных промежутках:
1.
.
2.
3.
.
Ответ:
2.
4.6. Иррациональные уравнения
Определение 4.10. Иррациональное уравнение – это уравнение, в котором переменная содержится под знаком корня или под знаком операции возведения в дробную степень.
Замечание 4.5. Корни четной степени, входящие в уравнения, считаются арифметическими (то есть подкоренное выражение должно быть неотрицательным и при этом значение корня также является неотрицательным). Подкоренное выражение корней нечетной степени может принимать любое действительное значение и в зависимости от знака корни могут принимать как отрицательные, так и неотрицательные значения.
К основным методам решения иррациональных уравнений относятся:
1. возведение обеих частей уравнения в одну и ту же степень:
a)
,
,
в частности для
,
б)
,
,
в частности для
,
;
2. введение новой переменной.
Пример 4.29. Решить
уравнение
.
Решение.
.
Ответ: .
Пример 4.30. Решить
уравнение
.
Решение.
Ответ:
;
1.
Пример 4.31. Решить
уравнение
.
Решение. Введем
новую переменную
,
,
тогда исходное уравнение примет вид:
.
Делая обратную
подстановку, получаем
.
Ответ:
.
Пример 4.32. Решить
уравнение
.
Решение.
.
Ответ:
.
Пример 4.33. Решить
уравнение
.
Решение.
Ответ:
.
Пример 4.34. Решить
уравнение
.
Решение.
.
Ответ:
.
Рассмотрим далее иррациональные уравнения, содержащие два или три корня третьей степени. Обычно при решении таких уравнвений используют два способа: 1) метод «замены»; 2) метод составления системы уравнений.
Замечание 4.6. В методе «замены» используются не тождественные преобразования уравнений, а переход от уравнения к следствию. Поэтому после решения уравнения данным способом необходимо сделать проверку полученных решений.
Пример 4.35. Решить
уравнение
.
Решение. Решим данное уравнение указанными выше способами.
Способ 1 (метод «замены».) Возведем обе части уравнения в куб, тогда имеем
.
Замним сумму
на 1, тогда получим уравнение
.
Снова возведем обе части уравнения в куб
.
Проверкой убеждаемся,
что
не является решением уравнения.
Следовательно, данное уравнение решений
не имеет.
Способ 2. Рассмотрим
решение данного уравнения
методом составления системы.
Пусть
;
,
тогда
или, снова делая ту же замену, получим
По теореме Виета
числа
и
должны быть корнями квадратного уравнения
,
но оно корней не имеет.
Ответ: решений нет.
Пример 4.36. Решить
уравнение
.
Решение. Запишем
уравнение в виде
и рассмотрим функцию
.
Данная функция представляет собой
композицию монотонно возрастающих
функций, поэтому также является монотонно
возрастающей. Следовательно,
Ответ:
.