5.1.2 Построение изображения в тонкой линзе

Для построения изображения точки в линзе необходимо найти точку пересечения любых двух лучей, проходящих через эту точку и линзу. Если такая точка пересечения существует, то полученное изображение называется действительным. В противном слу­чае, когда эти лучи расходятся, изображение находится в точке пересечения продолжений этих лучей, а изображение называется мнимым.

Мнимое изображение можно увидеть или сфотографировать, только если занять определенную позицию наблюдения, чтобы лучи после линзы попали в глаз наблюдателя. Иначе говоря, для наблюдения мнимого изображения нужен дополнительный оптический инструмент.

Основанный на вышеперечисленных свойствах тонких линз алгоритм построения изображения точки приведен в таблице и на рис.9

Алгоритм построения изображения точки в тонких линзах.

Собирающая линза	Рассеивающая линза
Провести луч, проходящий через точку и центр линзы
Провести через точку луч, параллельный главной оптической оси, до линзы. (прямая Аб на рис.9)
3. Продолжить луч по п.2 от линзы через ее фокус и далее (прямая бF на рис.9)	3. Провести линию от фокуса к (.)б (рис.9) и далее. Очевидно, что отрезок Fб это не луч, а его продолжение.
Точка пересечения луча, проходящего через центр линзы, и луча (или его продолжения), проходящего через фокус, есть изображение точки.

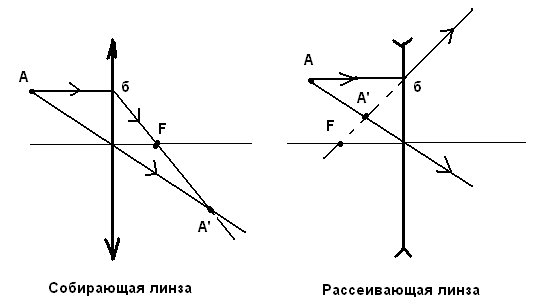
Рис.9

Очевидно, что если ход какого либо луча, проходящего через точку и линзу, зара­нее известен, то для построения изображения этой точки достаточно, например, провести прямую через точку и центр линзы. Пересечение этой прямой с известным лучом (или его продолжением) и есть изображение нашей точки (см. пример на рис.10).

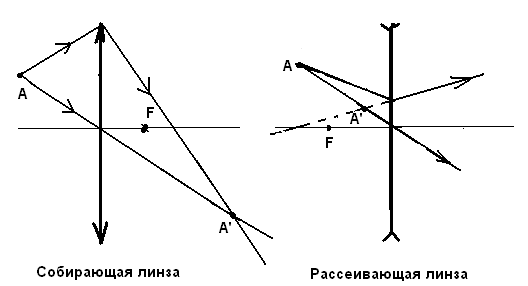
Рис.10

Для построения изображения предмета в линзе необходимо построить изображения всех характерных точек предмета расположенных со стороны линзы (ясно, что точки рас­положенные с другой стороны предмета изображений не дадут, так как падающие на них лучи не попадают в линзу). Примеры построения таких изображений приведены на рис.11.

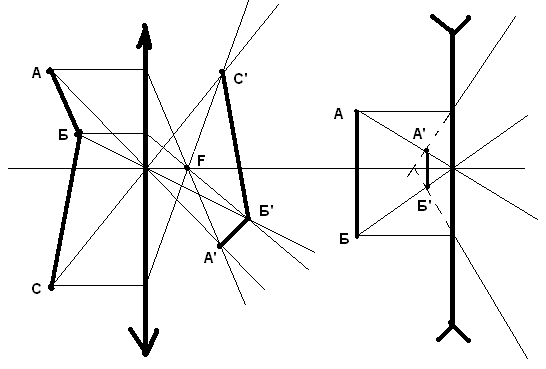
Рис.11

5.1.3 Свойства изображений в тонкой линзе

Из рис.9-11 нетрудно догадаться, что изображение в рассеивающей линзе всегда мнимое и прямое.

Так как мы рассматриваем только симметричные линзы, то очевидно, что и фокусы таких линз расположены симметрично относительно линзы. Будем называть фокус, расположенный со стороны предмета передним, а расположенный с другой стороны линзы – задним.

Свойства изображения в собирающей линзе зависят от положения предмета отно­сительно ее переднего фокуса. В этом нетрудно убедиться, если построить, например, изображения спички, стоящей на главной оптической оси на расстоянии от линзы меньше фокусного, немного дальше фокуса и на расстоянии больше, чем удвоенное фокусное расстояние (фокусное расстояние – это расстояние от фокуса до оси линзы). Если построения выполнены правильно, то из них видно, что:

- если предмет расположен ближе к линзе, чем фокус, то изображение получается мнимым, прямым (т.е. не перевернутым) и увеличенным;

- если предмет расположен за передним фокусом, но ближе чем удвоенное фокусное расстояние, то его изображение действительное, перевернутое и увеличенное.

- - если предмет расположен за удвоенным фокусным расстоянием, то его изображение действительное, перевернутое и уменьшенное.