5. Эффект Допплера

Пусть источник волн неподвижен и находится в точке И – рис. 24. Источник колеблется с частотой ν₀ и излучает волны с длиной волны . На рис. 25 круги показывают положение пучностей. Расстояние между соседними кругами (пучностями) отвечает длине волны λ₀.

Через приемник П за 1 сек. Пройдут волны и удалятся на расстояние с. Подсчитаем число пучностей (число волн), прошедших через приемник за 1 секунду.

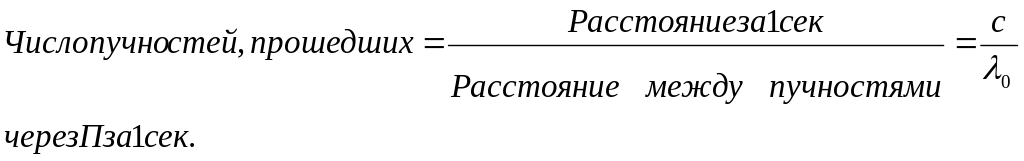
Следовательно, при покоящемся приемнике .

Положение фронта волны в момент времени t₀ (а) и через одну секунду после этого (б; в). Приемник покоится (а, б) и движется (в).

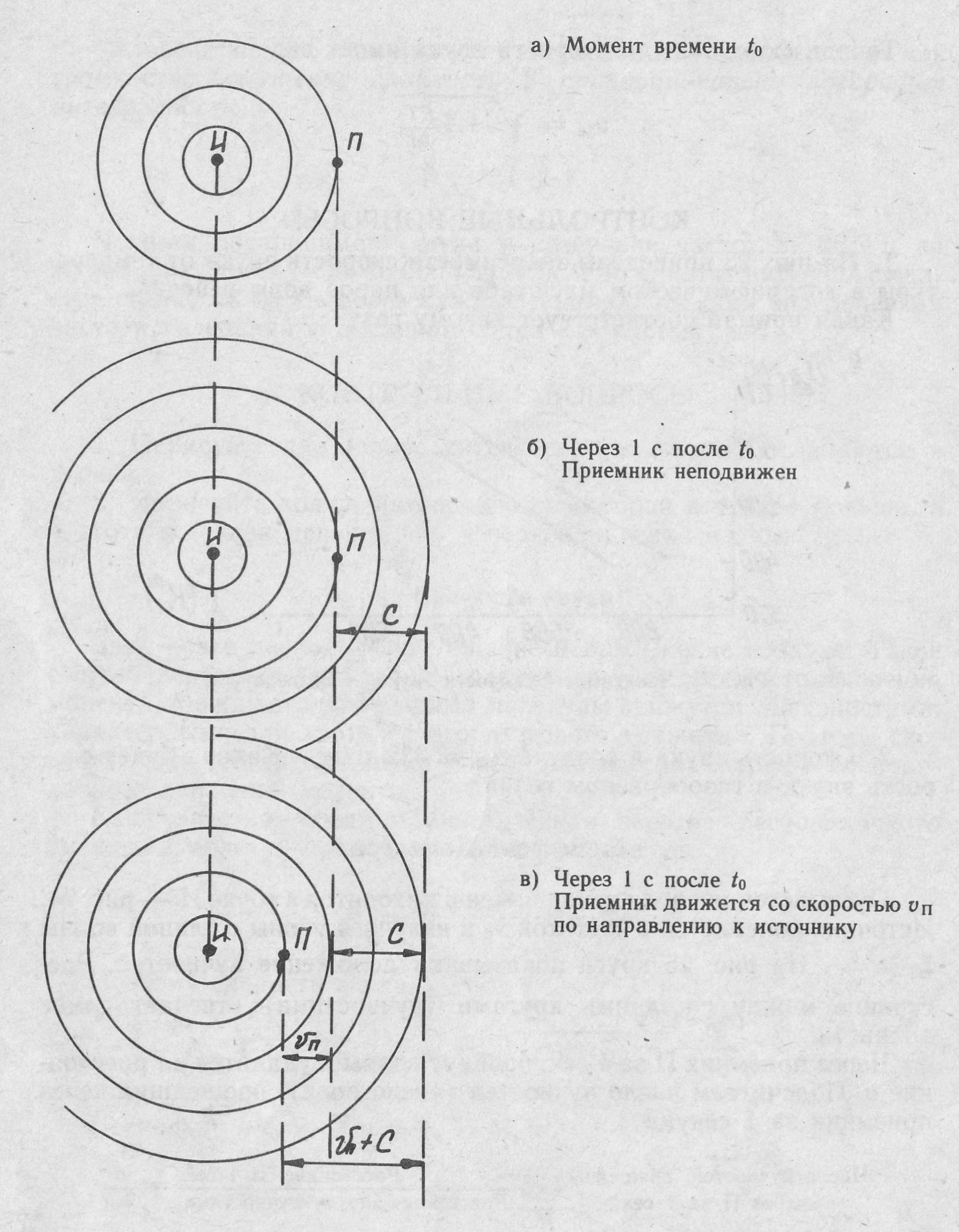
Рис. 24. Распространение волн от неподвижного источника

Если приемник П движется к источнику И со скоростью υ_П, то через приемник за одну секунду проходит число горбов, равное . Это число горбов, встречаемых за 1 секунду, есть кажущаяся частота

.

Поскольку , то .

Если приемник удаляется от источника, то . Зависимость частоты ν от скорости движения приемника показана на рис. 25.

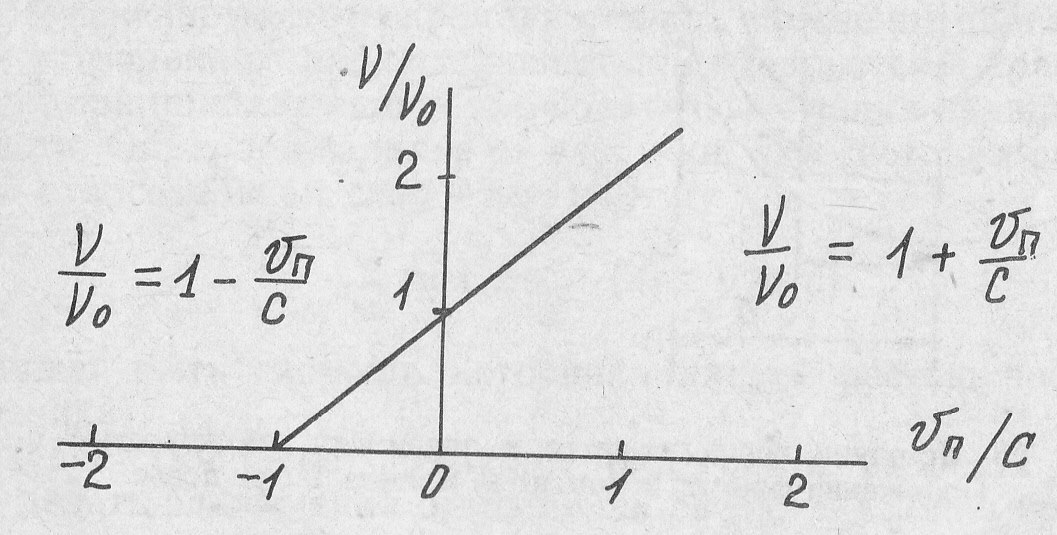
Рис. 25. Зависимость кажущейся частоты ν от скорости

движения приемника υ_П

Зависимость частоты от скорости движения приемника называется эффектом Допплера.

Рассмотрим теперь случай, когда приемник неподвижен, а источник волн движется к приемнику со скоростью υ_И. Пусть сначала расстояние между источником и приемником равно с, так что за 1 сек. Фронт достигнет приемника (см. рис. 26).

За 1 секунду источник испускает ν₀ волн (ν₀ горбов). Как видно из рис. 26, они расположатся на участке (с – υ_И). Поэтому, с точки зрения приемника, длина волны равна

или

.

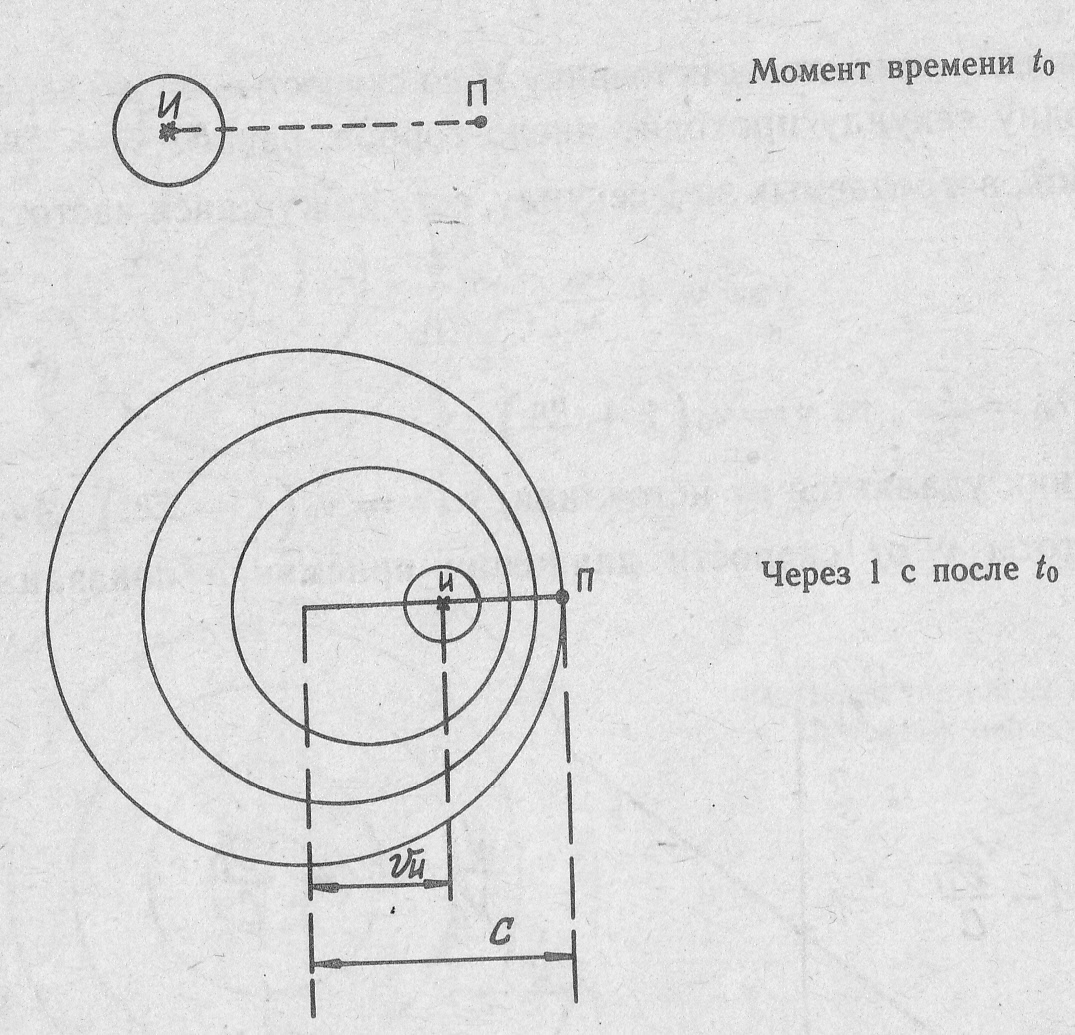
Рис. 26. Источник волн движется к приемнику со скоростью υ_И.

Положение фронта в момент t₀ и через 1 сек. После

Зависимость частоты ν от скорости движения источника показана на рис. 27.

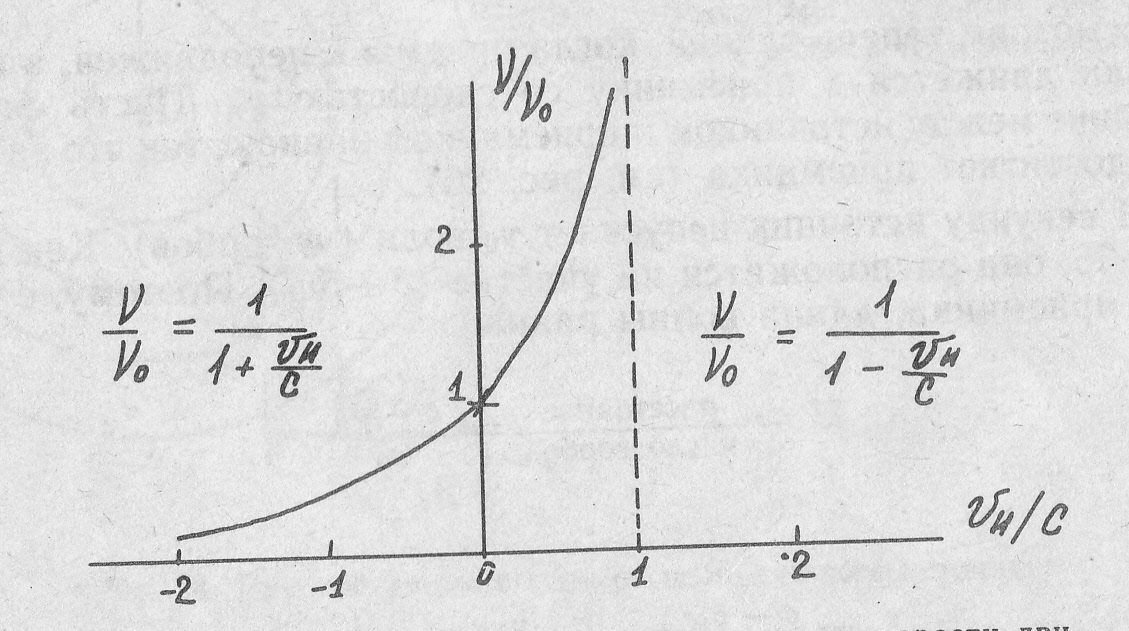
Рис. 27. Зависимость кажущейся частоты ν от скорости

движения источника υ_И

Если движутся источник звука и приемник, то воспринимаемая частота рассчитывается по формуле

.

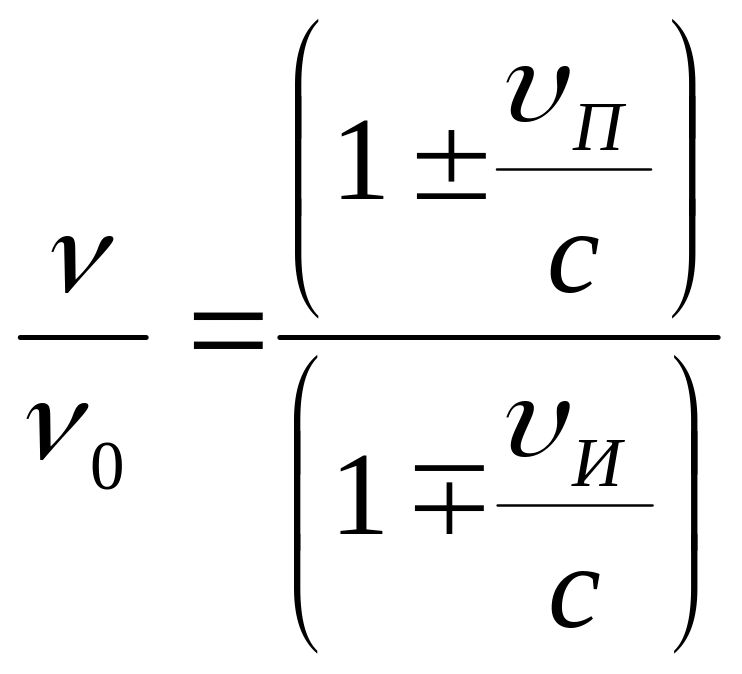6. Эффект Допплера для световых волн

В разделе «Волны» уже говорилось, что частота воспринимаемых колебаний зависит от скорости движения источника колебаний и скорости движения наблюдателя.

Аналогичный эффект Допплера наблюдается и для световых волн. Изменение частоты проявляется как изменение цвета. При движении источника от наблюдателя линии смещаются к красной части спектра, при приближении к наблюдателю – линии смещаются к синей части. Однако, в отличие от акустики, для световых волн важна только относительная скорость. Поэтому

(при  << c)

и  может быть скорость источника или скорость наблюдателя (приемника).

Явление Допплера позволяет определять скорость движения звезд, делать заключения о вращении звезд, т.к. один край звезды движется навстречу Земле, а другой – от нее.

Кроме того, атомы и молекулы светящегося газа находятся в быстром тепловом (хаотическом) движении. Атомы, движущиеся от наблюдателя, дадут линии, смещенные в красную часть спектра; атомы, движущиеся к наблюдателю, дадут линии, смещенные в фиолетовую сторону. Величина смещения тем больше, чем больше скорость и, следовательно, чем больше температура. Поэтому по смещению линий можно судить о температуре.