7. Явление резонанса
Рассмотрим формулу, описывающую колебания под действием внешней силы F = F0cos(ωt)
(5)
При малой частоте внешней силы ω << ω0
и, следовательно, тело колеблется с частотой внешней силы и постоянной амплитудой A0 = F0/k.
График зависимости внешней силы и смещения под действием этой силы при ω << ω0 показан на рис. 14.
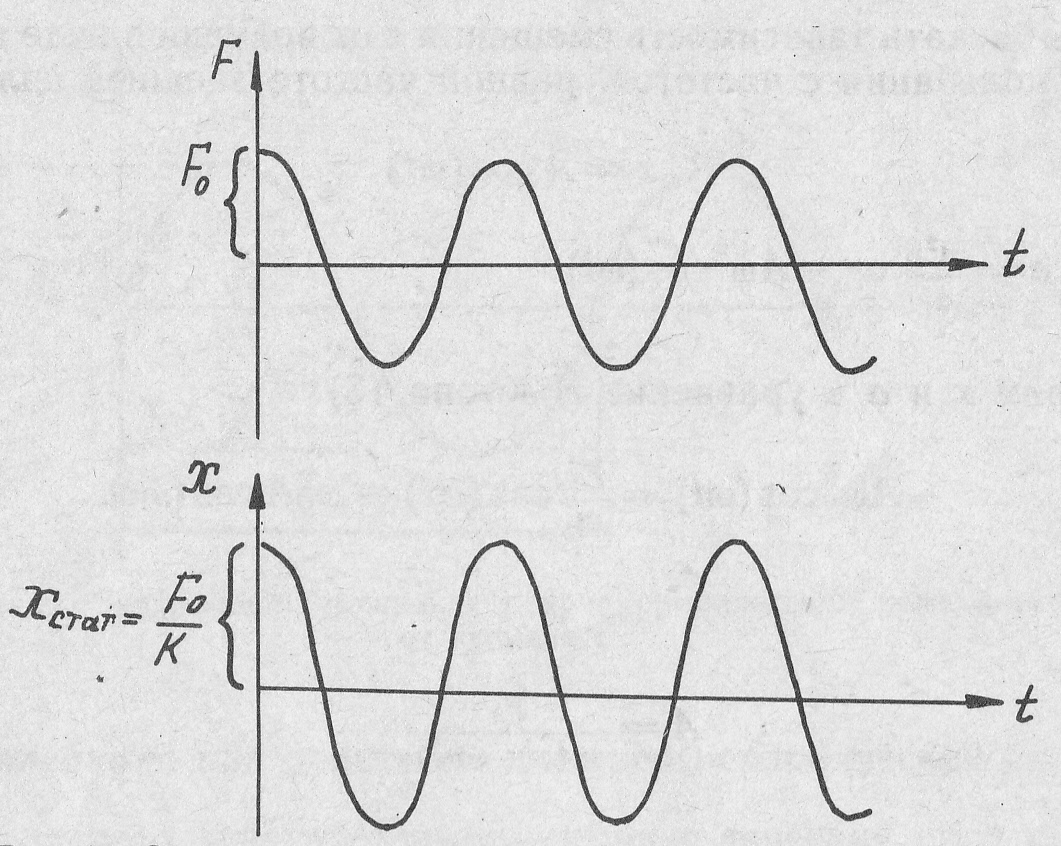
Рис. 14. Зависимость внешней силы F и смещения х
от времени t при ω << ω0
При большой частоте внешней силы ω >> ω0 формула (5) принимает вид
и колебания происходят в фазе, противоположной колебанию вынуждающей силы. Когда смещение положительно, вынуждающая сила отрицательна и наоборот. Амплитуда вынужденных колебаний убывает с ростом частоты вынуждающей силы
.
При ω ≈ ω0 амплитуда вынужденных колебаний сильно возрастает (становится бесконечной) (рис. 15).
Рис. 15. Зависимость смещения х от частоты внешней силы
при собственной частоте колебаний ω0
Совпадение частоты внешней вынуждающей силы с собственной частотой колебания системы называется явлением резонанса. Оно сопровождается резким увеличением амплитуды колебаний.
В реальных системах отклонения х не могут быть бесконечно велики. При больших х закон Гука перестает быть справедливым и амплитуда остается конечной.
Явление резонанса проявляется в совпадении спектров излучения и спектров поглощения. Тело поглощает колебания такой частоты, с которой само колеблется. Этот факт иногда формулируют так: система поглощает то, что сама испускает.
Явление резонанса используют для анализа частоты внешней вынуждающей силы. Для этого следует иметь систему резонаторов и подвергнуть её воздействию силы. В тех резонаторах, собственные частоты которых совпадут с частотой действующей внешней силы, возникнут интенсивные колебания. Такие резонаторы показаны на рис. 16.
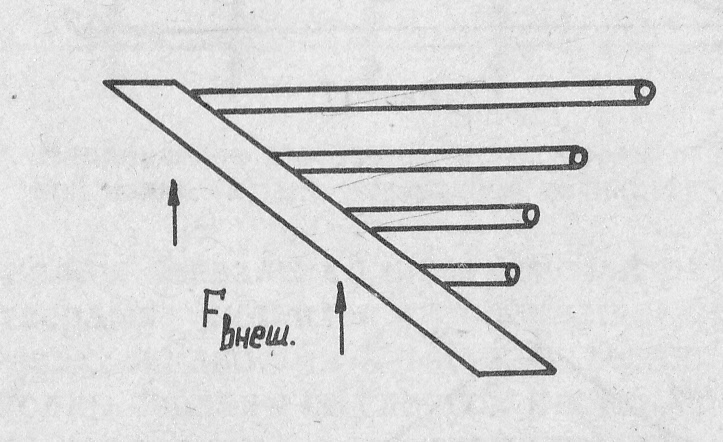
Рис. 16. Система резонаторов для определения
частоты внешней силы
Подобная система резонаторов имеется в ухе, позволяя анализировать звуковые колебания.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какой из графиков рис. 17 (а, б) представляет зависимость амплитуды смещения от частоты вынуждающей силы, а какой – зависимость амплитуды скорости?
2. Для двух систем получены резонансные кривые 1 и 2 (см. рис. 18). Каким одним параметром (масса тела, коэффициент упругости, амплитуда вынуждающей силы) отличаются эти системы?
Рис.17
Рис. 18. Зависимость смещения от частоты внешней силы
для двух систем
Занятие № 2. ВОЛНЫ
1. Продольные и поперечные волны
Волной называется процесс распространения колебаний в среде. Волна вовлекает окружающую среду в движение. Линия, которая указывает направление распространения волны, называется лучом. Если частицы среды колеблются вдоль направления распространения волны (вдоль луча), то волна называется продольной. Если же частицы среды колеблются перпендикулярно лучу – волна называется поперечной. Поперечная и продольная волны представлены на рис. 19.
Рис. 19. Направление колебаний частицы среды
в продольной волне (а) и в поперечной волне (б)
Продольные волны связаны со сжатием или растяжением среды и могут быть в твердых, жидких и газообразных средах. Примером служит звук в газах, жидкостях и твердых телах.
Поперечные волны связаны со сдвигом частиц среды и могут быть только в твердых телах или на поверхности жидкости. Примером служат волны, бегущие по шнуру, или морские волны.
Точки пространства, до которых в данный момент времени дошел волновой процесс, называются фронтом волны. Фронт перемещается вперед со скоростью распространения волны с.
Нарисуем волну (рис. 20). Для этого полезно представить фотографию моря в данный момент времени. Волна – это смещение точек среды х, находящихся на разных расстояниях от источника в некоторый фиксированный момент времени t.
Рис. 20. Зависимость смещения точек среды х
От расстояния до источника (r) волн
В другой момент t + τ волна будет иметь вид, показанный на рис. 21 пунктиром.
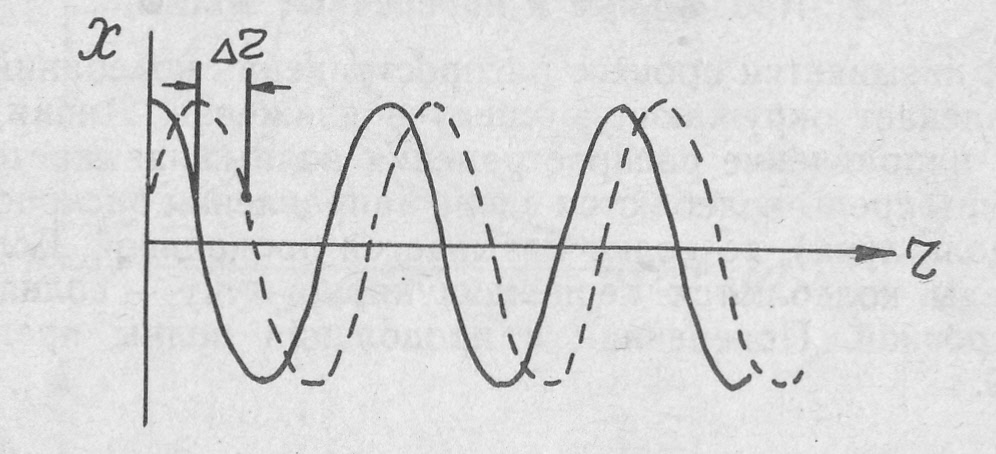
Рис. 21. Зависимость смещения х в момент времени t
(сплошная линия) и в момент времени t+r (пунктир)
от расстояния до источника волн (r)
Расстояние между точками среды, имеющими одинаковое смещение, называется длиной волны λ.