In the first case the result will be the vector –column with the elements

(2.4)

(і=1, 2,..., m) , and in the second case – the vector- line with the elements

. (2.5)

According to the term the matrix scalar product only the square matrix can be exponentiated into the integral positive rate:

А ^k=((АА)А)…А) (2.6)

k- factors

2.1.3 Matrix Transposition

If to replace the lines of the matrix A with the size mn by the corresponding columns, we will get the matrix А with the size nm which is called the transposed one relative to the matrix A.

Thus,

_ij^T= _ji

(i=1,2,…,n; j=1,2,…,m).

2.1.4 Matrix Norms

The norm of the matrix A=[a_ij] is the real number ||A|| which meets the following requirements:

- ||A||≥0 (and ||A=0|| only when А=[0]),

• ||A||=||*||A||, where  - the real number (and ||-A||=||A||),

• ||A||+||B||≥||A+B||,

• ||AB||||A||*||B||,

• ||A-B||≥|||B||-||A|||.

The following three norms are considered the easiest to compute :

(2.7)

The maximum sum of the matrix element modules in the lines;

(2.8)

The maximum sum of the matrix element modules in the columns;

(2.9)

Square root of the sum of the squares of the modules of all matrix elements.

2.2 Tasks

Do the operations with matrices according to the phrases given in the table 2.1. The repeated actions should be presented as separate procedures:

, , , .

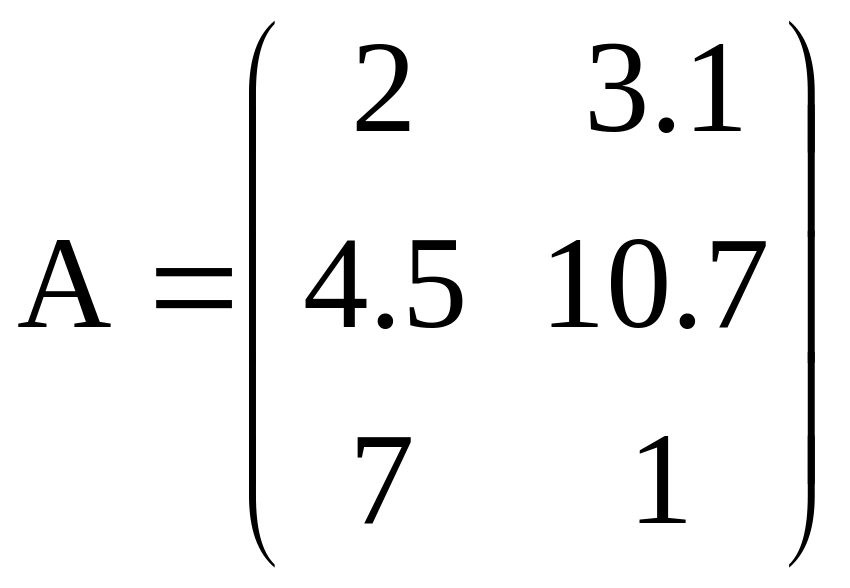Table 2.1

Number of the variant	Tasks
1	2
1	Check the correlations:: ||A+C||1 ||A||1+||C||1
2	||A*B||1 ||A||1*||B||1
3	||A-C||1 | ||C||1-||A||1 |
4	||A+C||2||A||2+||C||2
5	||A*B||2||A||2*||B||2
6	||A-C||2 | ||C||2-||A||2 |
7	||A+C||3||A||3+||C||3
8	||A*B||3||A||3*||B||3
The continuation of the table 2.1
1	2
9	||A-C||3 | ||C||3-||A||3 |
10	Compute: K=A+C+BT
11	K=B(A+C)+D
12	K=(A-C)*(D*B)
13	K=BT-A-C
14	K=B*A*B
15	L=||A+C||1+||B||1
16	L=||A||1+||B||2+||C||1
17	K=C*D+A+C
18	K=B*C*D
19	||A||1 ||AT||1 ||B||1 ||BT||1
20	K=D*CT*A
21	K=D-B*C-B*A
22	K=AT+CT+B
23	K=(A-C)*B
24	K=C*D-A-C