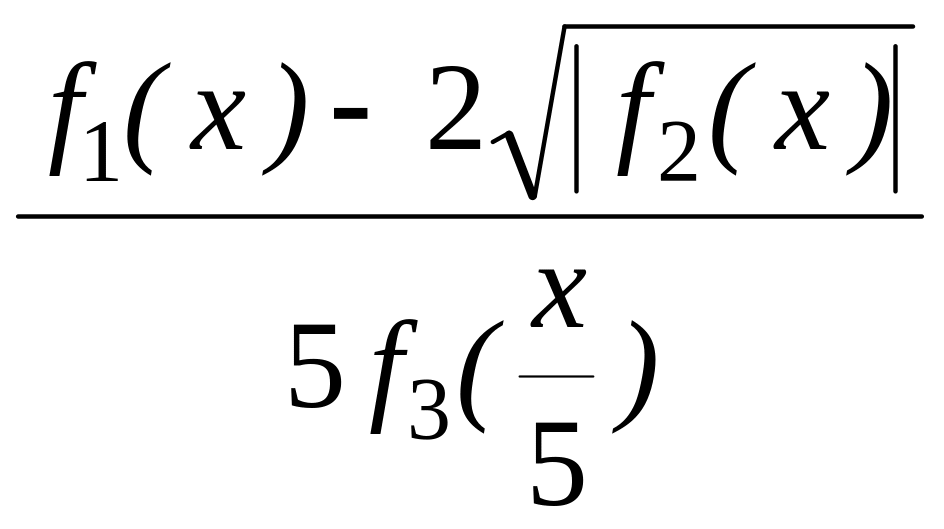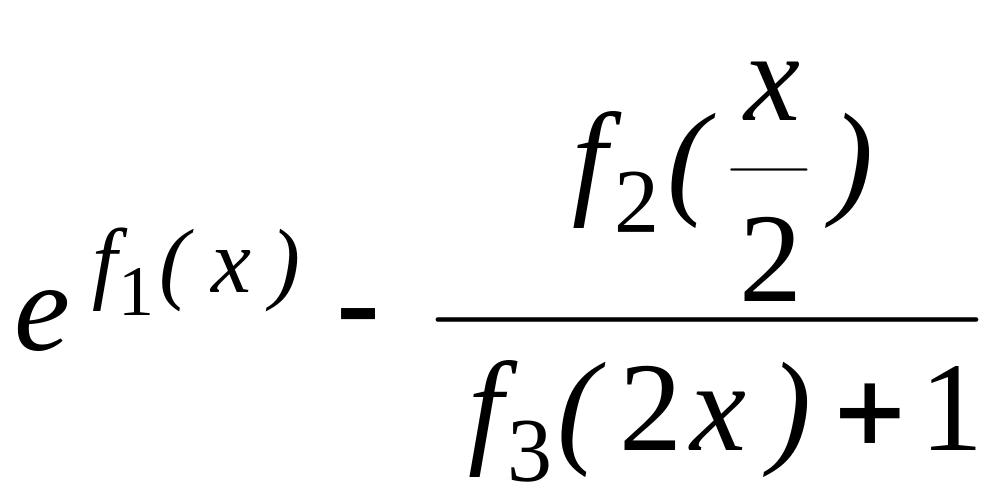МІНІСТЕРСТВО ОСВІТИ ТА НАУКИ УКРАЇНИ

ДОНЕЦЬКИЙ НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ

МЕТОДИЧНІ ВКАЗІВКИ

ДО ЛАБОРАТОРНИХ РОБІТ З КУРСУ

“МАТЕМАТИЧНІ МЕТОДИ І МОДЕЛІ ”

ДОНЕЦЬК – ДонНТУ – 2002

МІНІСТЕРСТВО ОСВІТИ ТА НАУКИ УКРАЇНИ

ДОНЕЦЬКИЙ НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ

МЕТОДИЧНІ ВКАЗІВКИ

ДО ЛАБОРАТОРНИХ РОБІТ З КУРСУ

“МАТЕМАТИЧНІ МЕТОДИ І МОДЕЛІ”

Затверджено

на засіданні кафедри

“Електропостачання

промислових підприємств і міст”

Протокол № 3/02

від 27.02.2002 р.

Затверджено

на засіданні навчально-видавничої

ради ДонНТУ

Протокол № 3

від 03.04.2002 р.

ДОНЕЦЬК - ДонНТУ - 2002

УДК 681.332(07)

Методичні вказівки до лабораторних робіт з курсу “Математичні методи і моделі” (для студентів спеціальності 7.090603 “Електротехнічні системи електроспоживання”) /Склад.: Джура С.Г., Шлепньов С.В., Якімішина В.В.

Викладено теоретичні зведення по методах обчислювальної математики, що використовуються при рішенні інженерних задач в області електротехніки й енергетики. Приведено завдання і методичні рекомендації до виконання 16 лабораторних робіт, призначених для навчання студентів методам рішення на ЕОМ лінійних і нелінійних рівнянь і їхніх систем, диференціальних рівнянь, методам чисельного інтегрування, апроксимації функцій, пошуку екстремальних значень.

Складачі: С.Г.Джура, доц.

С.В.Шлепньов, доц.

В.В.Якімішина, ас.

Рецензент: В.М.Павлиш, проф.

Нормоконтролер: В.І.Чурсінов, доц.

ВСТУП

Одним з головних напрямків науково-технічного прогресу в даний час є розвиток методів і засобів інформатики й обчислювальної техніки.

Використання математичних методів рішення інженерних задач на ЕОМ дозволяє значно підвищити ефективність процесів проектування, розрахунку параметрів, дослідження, аналізу і синтезу різних технічних систем, у тому числі і систем електропостачання.

У математичному плані багато задач електротехніки й енергетики зводяться до рішення алгебраїчних, трансцендентних і диференціальних рівнянь і їхніх систем, операціям над матрицями, векторами і рядами, апроксимації табличних функцій, мінімізації функціоналів та ін. Ці задачі не завжди можуть бути вирішені аналітично і вимагають застосування чисельних методів.

У даному посібнику приведені завдання і методичні вказівки до лабораторних робіт, виконання яких дозволить придбати навички алгоритмізації, програмування і рішення на ЕОМ задач з використанням методів обчислювальної математики.

За узгодженням з викладачем допускається заміна завдань, передбачених у лабораторних роботах, задачами аналогічного змісту з дисциплін, що паралельно вивчаються, або за тематикою НДРС, а також вибір мови програмування, якою буде виконуватися завдання.

Лабораторна робота 1 обчислення значень статечного полінома за схемою горнера

Мета роботи: навчитися обчислювати значення статечних багаточленів найбільш економічним образом, придбати навички програмування з використанням функцій і підпрограм користувача.

1.1 Теоретичні відомості

У практиці аналізу і синтезу систем автоматичного керування й у теорії електричних кіл часто виникає необхідність в обчисленні функцій, що мають вид статечного полінома (багаточлена):

P_n(x)=а₀ xⁿ+а₁ x^n-1+…+а_n-1x+а_n= , (1.1)

де n - ступінь полінома;

=(а₀, а₁, …, а_n)- вектор коефіцієнтів,

х - незалежна змінна.

Багаточлен (1.1) можна перетворити до виду:

P_n(x)=(…((( ₀x+ ₁)x+ ₂)x+ ₃)x+…+ _n) . (1.2)

Алгоритм обчислення P_n(x), складений на підставі виразу (1.2), називається схемою Горнера.

Відповідно до цієї схеми багаточлен і-го порядку виражають через багаточлен (і-1)-го порядку за формулою

P_i=P_i-1x+ _i. (1.3)

Поклавши P₀=а₀ і виконавши операцію (1.3) n разів при і=1,2,...,n, одержують необхідне значення.

У математиці доведено, що для багаточленів загального виду не можна побудувати алгоритм більш економічний у значенні числа операцій (n додавань і n множень), ніж схема Горнера.

1.2 Завдання

Розрахувати значення змінної z при x, що змінюється від -1 до +1 із кроком 0,1. Вирази для обчислення z приведені в таблиці 1.1. У цих виразах функції f₁(x), f₂(x) і f₃(x) являють собою статечні багаточлени, що відрізняються друг від друга порядком і значеннями коефіцієнтів.

Для непарних варіантів:

f₁(x)=1.07x⁵-12x⁴-2.8x³+6.3x²+3.7x+4,

f₂(x)=10.1x⁷+37x⁵-15x⁴+8.2x+5.4,

f₃(x)=-23x³+13.6x²+0.5x-1.2.

Для парних варіантів:

f₁(x)=8.16x⁴+14x³+0.9x²+3.8x-2,

f₂(x)=19.7x⁶+11.4x⁴+2.3x³-1.8x+0.9,

f₃(x)=21.6x⁵-17.4x⁴+8.7x³+11x.

Для введення значень коефіцієнтів статечних багаточленів скласти підпрограму (процедуру), а для обчислення цих багаточленів - функцію користувача.

Таблиця 1.1 – Вихідні дані до лабораторної роботи №1

Варіант	Вираження для обчислення змінної
1	2
1,2
3,4
5,6
7,8
9,10
11,12
13,14
15,16
17,18
Продовження таблиці 1.1
1	2
19,20
21,22
23,24
25,26

1.3 Методичні рекомендації

Якщо програма складається мовою програмування Паскаль, масиви коефіцієнтів для функцій f₁(x), f₂(x) і f₃(x) у програмі і масив коефіцієнтів для обчислення значення статечного полінома P_n(x) у функції користувача повинні мати однаковий тип, описаний у головному модулі, наприклад,

const nmax=6;

type vector=array[1..nmax] of real,

де nmax - максимальний порядок багаточлена.

Перераховані вище масиви краще позначити різними ідентифікаторами.