4.2.2. Оцінювання стійкості за критерієм Михайлова

Критерій Михайлова належить до частотних критеріїв стійкості. Для визначення стійкості необхідно побудувати годограф вектора Михайлова, котрий є характеристичним поліном системи при заміні оператора р на . Система стійка, якщо годограф Михайлова при зміні кругової частоти починається на речовій осі та проходить послідовно крізь n квадрантів (n - порядок характеристичного полінома) в позитивному напрямку(проти часової стрілки).

Характеристичне рівняння для заданої САК

Після підстановки

Виділяємо речову та уявну складові

Знаходимо точки перетинання годографа с речовою осью

Вирішив рівняння, отримаємо наступні корені:

Так як годограф будується в діапазоні , то негативні корені відкидаємо.

Розрахуємо координати точки перетинання з дійсною осью.

Знаходимо точки перетинання годографа с уявною осью:

Вирішив рівняння, отримаємо наступні корені:

Використовуючи тільки позитивні значення частоти , знайдемо координату точки перетинання з уявною осью

Нанесемо точки перетинання на комплексну площину (см. рис. 4.7) та з'єднав їх плавною кривою в порядку зростання кругової частоти . Так як годограф проходить послідовно крізь три квадранта і порядок характеристичного рівняння також дорівнює n=3, то задана система стійка.

Годограф Михайлова, що представлено на рис. 4.7, отриман в середовище пакета програм Mathcad 14.

Рис. 4.7 Годограф Михайлова

4.3. Визначення часових та частотних характеристик

4.3.1. Визначення часових характеристик

Якщо передавальна функція САК

,

то за умови (порядок полінома чисельника не більше порядку полінома знаменника) та відсутності нульових коренів в характеристичному рівнянні перехідна функція може бути знайдена по формулі

де корені характеристичного рівняння;

а поліном в знаменнику

_.

Передавальна функція розглядаємої САК

.

Знайдемо корені характеристичного рівняння

в пакеті програм MATLAB за допомогою команди

roots([0.3 1.6 1.2 1]) .

Маємо

Знайдемо похідну характеристичного поліному

Визначимо

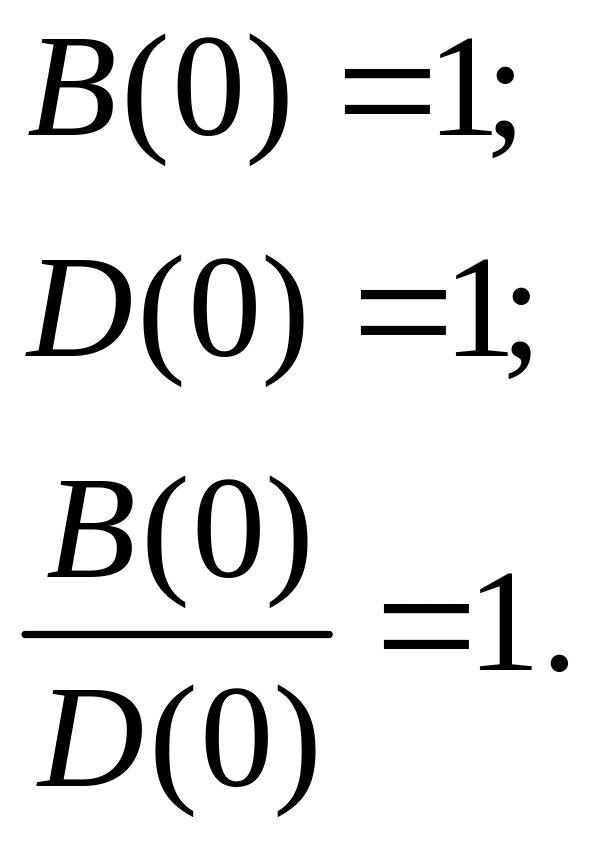
Обчислимо для кожного із трьох коренів.

Для першого кореня

Для другого кореня

Так як корені и є сполученими, то й вираження, що обчисленні для них також є сполученням комплексних величин.

Тому

Перейдемо до експоненційної форми запису комплексного числа згідно відношенню

_,

де величина повинна бути обчислена в радіанах.

Маємо

Підставивши знайдені величини в вираження для перехідної функції, отримуємо

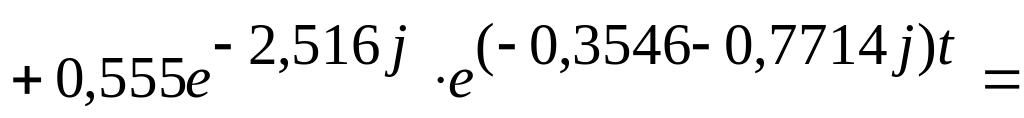
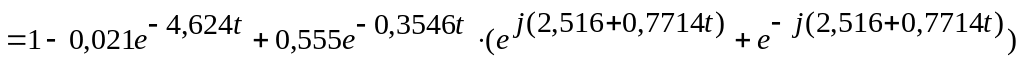
Застосовуя формулу Ейлера

_,

Отримуємо перехідну функциію

Перехідна характеристика показана на рис. 4.8 (графік отриман в середовищі пакета прикладних програм MATLAB).

h(t)

t

t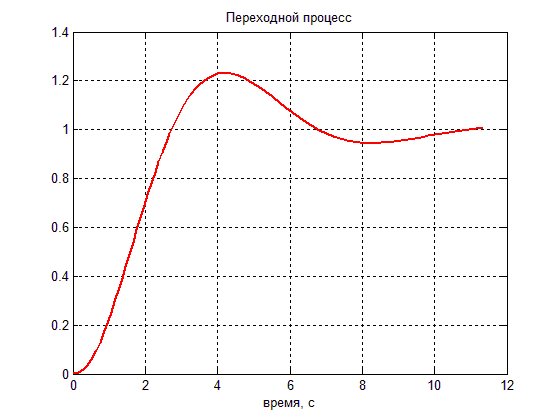

Рис. 4.8. Перехідна характеристика

Вагова функція є похідною від перехідної функції

.

_Маємо

Вагова характеристика приведена на рис. 4.9 (графік отриман в середовище пакета прикладних програм MATLAB).

ω(t)

t

t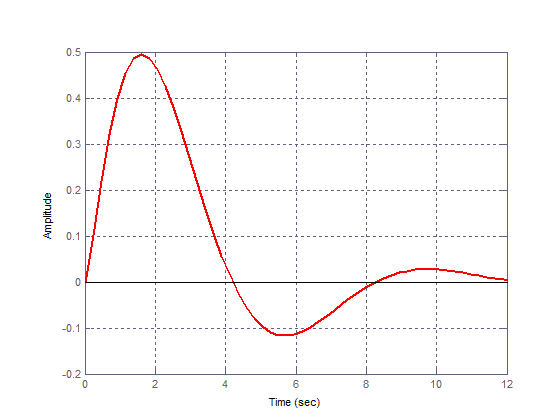

Рис. 4.9. Вагова характеристика