1.2.3 Геометрический метод определения вероятностей
Условия применения: Пусть пространство элементарных исходов вероятностного эксперимента непрерывно, и представляет собой некоторую область . Эксперимент состоит в том, что внутри области произвольным образом выбирается точка, причем вероятность попадания в любую часть А этой области пропорциональная мере этой части, и не зависит от ее расположения в области .
Тогда вероятность попадания точки в область А равна ............................ ......................................................................................................................................
…………………… (1)
где mes (A) - ………………………………………………………………. ……………………………………………………………………………………....
mes () -………………………………………………………………….......
Для одномерного пространства , формула (1) имеет вид:
………………………
Для двумерного пространства , формула (1) имеет вид:
………………………
Для трехмерного пространства , формула (1) примет вид:
………………………
Пример 4. (Задача о встрече)
Два студента договорились о встрече в определенном месте между 13 и 14 часами. Они договорились, что пришедший первым ожидает второго в течение 20 минут, и в случае его отсутствия, покидает место встречи. Предполагая, что все возможные варианты прихода студентов на место встречи в течение назначенного часа равновозможны, найти вероятность встречи этих студентов.
1.2.4 Статистический метод определения вероятностей.
Очевидно, что существует большой класс событий, вероятности которых нельзя вычислить с помощью классического или геометрического метода определения вероятностей.
Например:
– …………………………………………………………………………….
– …………………………………………………………………………….
– …………………………………………………………………………….
– …………………………………………………………………………….
– …………………………………………………………………………….
Естественно предположить, что каждое из таких событий обладает некоторой вероятностью (степенью возможности), которая при многократном повторении соответствующих опытов будет отражаться в относительной частоте событий.
Относительной частотой события A в некоторой серии из N испытаний называется ……………………………………………………………. ………………………………………………………………………………………………………………………………………………………………………………
………………………..
где NA – ……………………………………………………………………………. ………………………………………………………………………………………
N – ………………………………………………………………………………….
Установлено, что при увеличении числа испытаний относительная частота события A приближается к вероятности события A и стабилизируется около этого значения.
Согласно статистическому методу определения вероятности, в качестве вероятности события используется ............................................................. ......................................................................................................................................
Результаты подбрасываний монеты
Экспериментатор |
N |
NA |
|
Французский естествоиспытатель Жорж-Луи Леклер де Бюффон (1707-1788) |
|
|
|
Английский ученый-биолог Карл Пирсон (1857-1936) |
|
|
|
Английский ученый-биолог Карл Пирсон (1857-1936) |
|
|
|
График зависимости относительной частоты от числа испытаний, например, может иметь следующий вид:
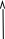
N
Пример 5. Согласно статистическим данным, в Республике Беларусь в 2010 году родилось 108050 детей (55714 мальчиков и 52336 девочек). За 6 месяцев (с января по июнь) 2011 года в городе Гомеле родилось 96 мальчиков и 94 девочки. На основании приведенных данных определить вероятность рождения мальчика в Республике Беларусь и в городе Гомеле.
Проверочный тест 5
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
|
|
|
|
|
|
|
|