1.1.3. Операции над событиями

Пусть рассматриваются два произвольных события А и В, каждое из которых в результате вероятностного эксперимента может произойти ли не произойти. Известны множества элементарных исходов, благоприятных осуществлению этих событий.

Суммой событий А и В (обозначается A  B или A + B) называется событие, состоящее из элементарных исходов, благоприятных ……………… ……………………………………………………………………………………..…Событие A  B состоит в осуществлении ..................................……………… …………………………………………………………………………………….….......................................................................................................................................

Аналогично определяется сумма конечного или счетного числа событий A₁  A₂  A₃  … Благоприятными этому событию являются все элементарные исходы, благоприятные ……………………….……………………. ……………………...... Это событие состоит в осуществлении ………………………………......................…………………………………………

Произведением событий А и В (обозначается A  B или AB) называется событие, состоящее из элементарных исходов, благоприятных осуществлению ………………………………………….............. Событие A  B состоит в ………………………………………………………………………………………

Произведение конечного или счетного числа событий А₁  А₂  А₃  … представляет собой событие, состоящее их элементарных исходов, благоприятных осуществлению …………………………………… …………….... Это событие состоит в .............……………………… …………………………….…………………………………………………………

Разностью событий А и В (обозначается A \ B, или A – B ) называется событие, состоящее из …………………………………………………………… ………………………………………………………… Событие A \ B состоит в том, что .........................................................………………………………………

В рассмотренном примере 1:

A  B состоит в …………………………………………………………. ……………………………………………………………………………………….................

A  B состоит в …………………………………………………………….................

A \ B состоит в ……………………………………………………………..................

A  B =  A  B =  A \ B =

A  С = A  C = A \ С =

С  B = С  B = С \ B =   

Противоположным событию А называется событие ......................., состоящее из .............................................................................................................. ......................................................................................................................................

Событие Ā состоит в том, что.......................................................................

В примере 1 противоположные к событиям А, В, С, D, Е:

………………………………………………………………………………

………………………………………………………………………………

………………………………………………………………………………

………………………………………………………………………………

………………………………………………………………………………

События А и В называются несовместными, если ............................

Т.е. несовместные события .......................................................................................

В примере 1 несовместными являются события ………………………

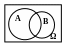
Пример 2. Геометрическая интерпретация операций над событиями. Производится испытание: в прямоугольнике, изображенном на рисунке, выбирается наугад точка. Пространством элементарных исходов  данного эксперимента является множество всех точек данного прямоугольника. Рассмотрим события: A – {выбранная точка попадет в область A}; B – {выбранная точка попадет в область B}.

Области, попадание в которые благоприятно событиям A, , A  B, A  B, A \ B, В \ А, изображены на следующих рисунках: