Доведення Кут між прямими (4) і (5) дорівнює куту між їх напрямними векторами і . На підставі формули скалярного добутку векторів і дістанемо

.

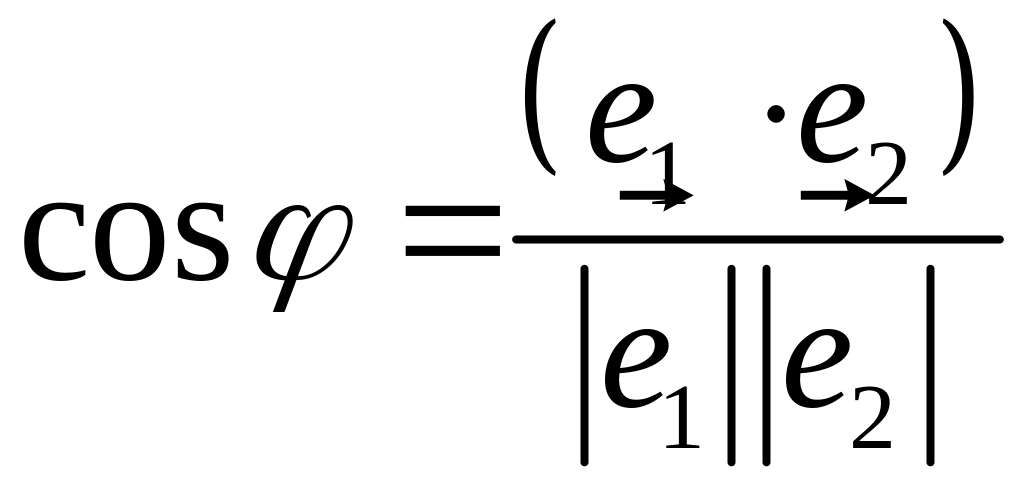Виразивши скалярний добуток і довжини векторів і через координати векторів, матимемо формулу (6), що й доводить теорему.

Умова перпендикулярності двох прямих: якщо прямі (4) і (5) перпендикулярні, то кут між напрямними векторами і прямий і відповідно , або в координатах

(7)

Умова паралельності прямих: прямі (4) і (5) паралельні тоді і тільки тоді, коли їх напрямні вектори і колінеарні

(8)

5. Відстань від точки до прямої Нехай задано таке рівняння прямої l

і точку .

Довжину перпендикуляра, опущеного з точки до прямої l, називають відстанню від точки до прямої (Рис. 2.7)

z M₁

d

M₀

у

0

х

Рис. 2.7

Визначимо відстань між точкою і прямою l. Шукана відстань d є висотою паралелограма, побудованого на векторах і . Нехай . Оскільки дорівнює площі паралелограма, то , тобто

.

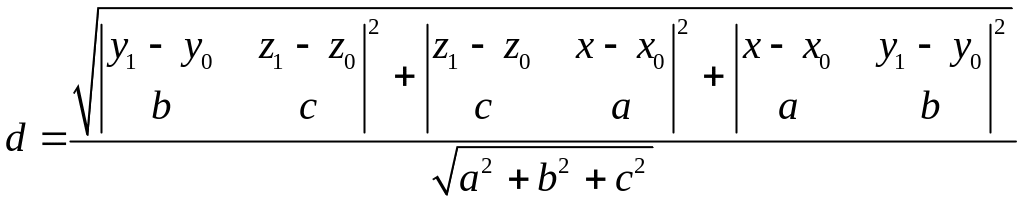2.6.6. Площина у просторі. Загальне рівняння площини

Нехай задано деяку площину Р, яка проходить через точку , і перпендикулярний до неї вектор (Рис 2.8).

Рис. 2.8

Вектор називається нормальним вектором площини Р. Щоб написати рівняння площини, візьмемо довільну точку на площині й побудуємо вектор . Тоді, в силу перпендикулярності вектора до площини Р, дістанемо . Виразимо умову взаємної перпендикулярності цих векторів через їх скалярний добуток: .

Оскільки

,

то матимемо

.

Це і є рівняння площини, яка проходить через задану точку перпендикулярно до вектора .

Перетворимо це рівняння до вигляду

Позначивши дістанемо загальне рівняння площини у просторі:

.

Звідси випливає, що площина у просторі описується рівнянням першого степеня відносно змінних

Справедливе і обернене твердження: будь-якому рівнянню першого степеня відносно змінних відповідає площина (і лише одна) у просторі.

Справді, рівняння з довільними коефіцієнтами, що не дорівнюють нулю одночасно, еквівалентне рівнянню

де – будь-який розв’язок першого рівняння. Відповідно ці два рівняння описують один і той самий геометричний образ. Але друге рівняння можна розглядати як умову взаємної перпендикулярності двох векторів:

і . За цієї умови вектор визначає площину , що проходить через точку . Відповідно рівняння описує ту саму площину .

2.6.7. Рівняння площини, що проходить через три задані точки

Нехай задано три точки , що не лежать на одній прямій. Складемо рівняння площини, що проходить через ці точки. Нехай – довільна точка шуканої площини (Рис. 2.9).

М₂

М₃

М

Рис. 2.9

Виберемо як основну будь-яку із заданих точок, наприклад , і побудуємо вектори . Оскільки точка М належать площині, ці вектори компланарні. Запишемо умову їх компланарності:

.

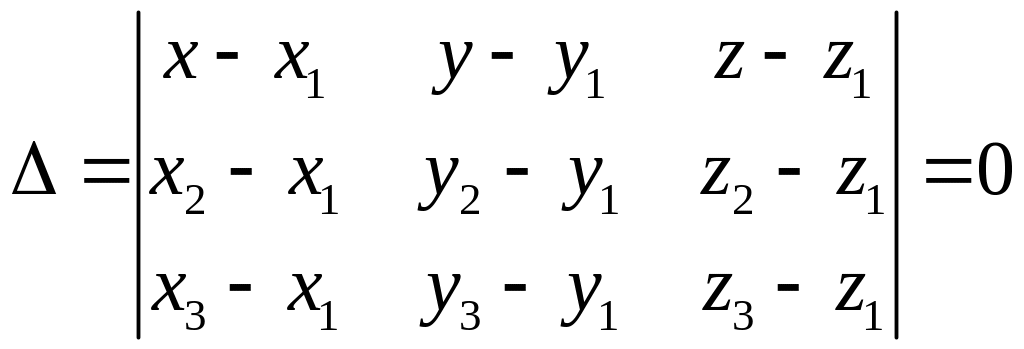Це і є рівняння площини, яка проходить через три задані точки. Обчисливши визначник, дістанемо це рівняння у загальному вигляді.