Для вільного вектора таке розвинення за базисом має вигляд

.

Вектори , а також , суми яких утворюють вектори і , називають складовими (або компонентами) векторів і відповідно.

Напрям вектора визначається кутами α, β і γ з осями координат Ох, Оу, Оz. Косинуси цих кутів (так звані напрямні косинуси вектора) визначаються за формулами

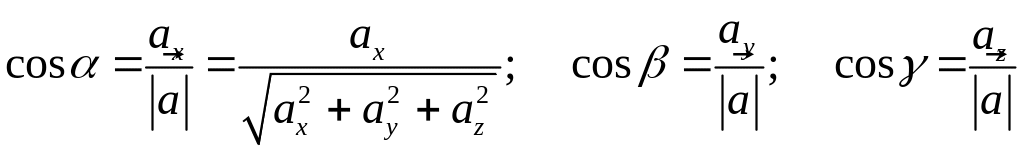
Напрямні косинуси вектора зв’язані співвідношенням

.

2.5. Дії над векторами

Наповню, що сума векторів і , початки яких співпадають, зображається вектором з тим же початком, який співпадає з діагоналлю паралелограма, сторонами якого є вектори і (Рис.2.5). Різниця цих векторів зображається вектором, який співпадає з другою діагоналлю того ж

Рис. 2.5

паралелограма, причому початок цього вектора знаходиться в кінці вектора , а кінець – в кінці вектора .

Якщо вектори і задано їх розвиненнями за базисом , то їх сума і різниця визначається формулами

Добуток вектора на скалярний множник т при цьому визначається так

.

Зокрема, якщо , де , то вектор має довжину, яка дорівнює одиниці, і напрям, який співпадає з напрямом вектора . Позначимо його . Знаходження одиничного вектора того ж напряму, що й даний вектор , називається нормуванням вектора .

Скалярним добутком двох векторів і називається число, яке дорівнює добутку довжин цих векторів на косинус кута φ між ними

.

Серед властивостей скалярного добутку двох векторів зазначимо такі:

1) оскільки кут φ у цьому разі дорівнює нулю;

2) якщо і перпендикулярні між собою, то ( );

3) - безпосередній наслідок визначення скалярного добутку.

Згідно з властивостями 1-3 для базисних векторів матимемо

Типовим прикладом скалярного добутку в механіці є, наприклад, формула роботи

,

де вектор - сила, точка прикладання якої (центр ваги тіла) переміщується з початку в кінець вектора .

Якщо вектори і задані своїми координатами

то скалярний добуток цих векторів знаходиться за формулою

,

а кут між векторами і -

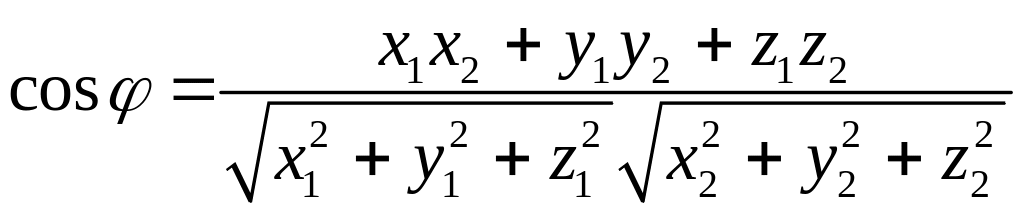. (1)

Приклад. У просторі задані три точки: і . Знайти кут .

А

φ

В

С

Обчислимо координати векторів і :

.

Тоді за формулою (1) матимемо

.

Отже .

Нехай

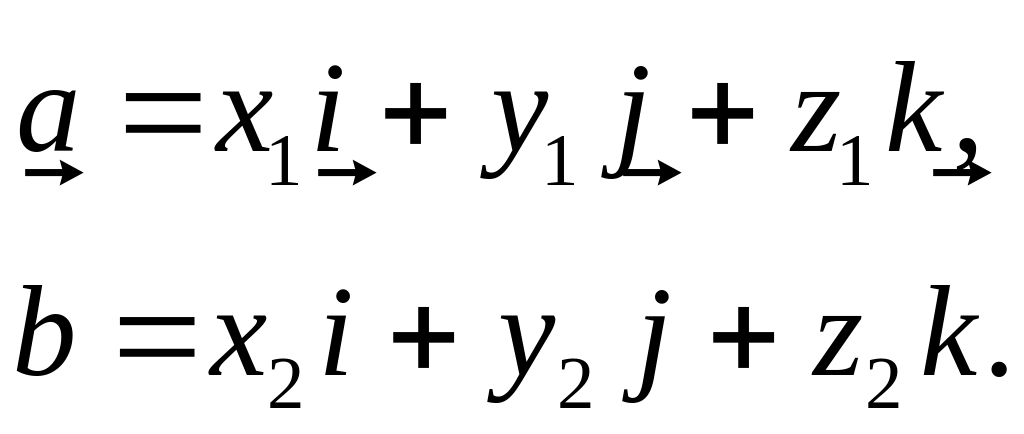
Тоді векторним добутком векторів і називається вектор

Серед властивостей векторного добутку зазначимо такі:

1).

якщо при обчисленні визначника діяти з векторами так, як з числами.

Щоб переконатися у справедливості цієї властивості досить розкрити визначник за першим рядком.

2).

3).

4).

5).

Властивості 2 – 5 є безпосередніми наслідками властивостей визначників.

6). і

Щоб переконатися у справедливості цих властивостей досить обчислити скалярні добутки і і переконатись, що вони дорівнюють нулю. Дійсно

, тому з властивості 2 скалярного добутку дістанемо , що й потрібно. Друга умова доводиться аналогічно.

7). , де – кут між векторами і .

Справді, оскільки , то ця рівність рівносильна рівності

але

за означенням скалярного добутку.

Щоб переконатися у справедливості одержаної рівності

досить перевірити рівність, яка з неї випливає,

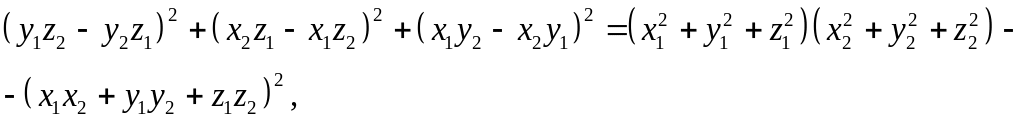
розкривши в ній дужки.

8). Для базисних векторів мають місце рівності

Ця властивість є наслідком означення векторного добутку, якщо врахувати, що

Типовим прикладом векторного добутку в механіці є, наприклад, формула для розрахунку моменту сили , прикладеної в точці М, відносно деякої точки простору О:

Приклад 1. Задані вектори і . Знайти довжину вектора

Згідно з означенням

Отже, , звідки

Мішаний добуток трьох векторів – це скалярний добуток векторного добутку двох перших векторів на третій, тобто

Обчислення мішаного добутку векторів і відбувається за формулою

Справді, за означенням векторного і властивістю скалярного добутків матимемо

Звідси, враховуючи формулу для обчислення визначника третього порядку, матимемо потрібне.

Серед властивостей мішаного добутку трьох векторів відзначимо властивість, що тоді і тільки тоді, коли вектори лежать в одній площині.